|
Thursday, February 07, 2008
Did you know that neurons have resonant properties? I didn't know that until I read this paper from the Johnston lab down in Austin, TX. Usually I think of synaptic transmission in terms of a single action potential or other event that releases neurotransmitter, so I don't end up in the frequency domain. But, of course, the pattern of release is just as important as the magnitude. Neurons can fire in rhythmic patterns that have additive effects downstream because of the principle of temporal summation. Neurons are continuously deciding whether to fire or not. In a simple view, they do this by summing the 'aye' and 'nay' votes across all inputs. Aye votes move the voltage potential across the neuronal membrane in a positive direction by allowing positive ions to flow into the cell. There is a time window in which an input can cast its vote and still be counted based on how long it takes the receiver neuron to respond to inputs and how long it takes to return to a clean slate after responding. This allows the same input to vote several times if it does so at just the right frequency. If it tries to go too fast it will run up against the membrane capacitance. You see, the membrane potential isn't exactly a count of the number of positive and negative charges inside and outside the cell. Rather, the ions have to be lined up right next to the membrane producing a capacitive current for the period of time it takes to push positive charges off the outside of the cell and line other ions up on the inside. People familiar with basic principles of electrical circuits know that charging a capacitor adds a time dimension. So if an input votes too fast, say, at a frequency of more that 10 to 20 Hz (I'm not sure of the exact number) the effect will be attenuated as the receiver simply can't add that fast.
On the other hand, firing too slow simply won't do either. Neurons have components that react to any change in membrane potential and push back toward baseline. Of particular interest is the H-conductance. The H-conductance is an ion channel in the membrane that allows positive ions to flow into the neuron (as long as the membrane potential is more negative than -30ish mV). Curses. I didn't want to, but I think I have to explain reversal vs. activation potential. Reversal: Ions want to flow to places where there is a lower concentration. They want room to spread out and have a nice big yard with a swingset for the kids and all that, but they also want to get away from other ions with the same type of charge. So if there were a bunch of K+ ions sitting inside a cell and only a few outside and a channel opened up they would want to go out, but if there are already a bunch of Na+ ions outside then they might think twice because there is too much positivity out there already. In other words, potential and concentration gradients are taken into consideration. SInce there is a lot of Na+ outside the cell, it wants to flow into the cell and drive the potential up. There is a lot of K+ inside a neuron, so it wants to flow out of the cell and drive the potential down. If you open a channel that allows both ions through they will arrive at a consensus (equilibrium, reversal) potential that accommodates everyone's needs. The H-conductance does just that and arrives at around -30 mV. If the membrane was at -30 mV, no net ion flow would occur. If it strays, the driving forces will push back towards -30. Normally, due to other considerations, a neuron sits near -55 to -60 mV, so activating the H-conductance will push the neuron toward a more positive potential. Now Activation: Ion channels respond to changes in membrane potential by opening and closing. The H-conductance is closed at positive potentials and becomes activated when the potential moves more negative than about -60 mV. This has the effect of opposing hyperpolarization, the increased difference in voltage across the membrane, because when the membrane tries to move more negative the channel opens and pushes positive. Since the activation potential for H-conductance is near the resting membrane potential, it can also oppose depolarization by shutting portion of channels and reducing the push towards positive. Finally, channel activation and inactivation takes time. It takes more time than charging the membrane capacitance. If an input wants to make a difference, it has to get its votes in before the H-conductance comes into play and brings everybody back to baseline. In this way, the H-conductance acts as a high-pass filter, only allowing speedy inputs to have a say. Now we have a window of input frequencies that can really strongly affect the cell. If they are too fast, they are filtered out by the membrane capacitance. If they are too slow, they are filtered out by the H-conductance. Really the H-conductance is just one type of conductance that might do the job. Any conductance that is activated near resting membrane potential and opposes change would work fine. You can measure how this plays out in a real cell using something called an impedance amplitude profile (ZAP). You measure the voltage change in a neuron as you inject current at different frequencies but constant amplitude. In practice, this is done really quickly as a sweep across the frequencies. The result is a peak voltage change that corresponds to the resonant frequency of the cell. Like so: 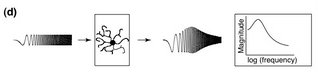 Narayanan and Johnston already knew that you could measure resonant properties of neurons. What we didn't know was that these properties varied in space and time. They measured resonance in CA1 pyramidal neurons. These are the major excitatory cells in an important region of the hippocampus, a brain structure responsible for memory encoding and spatial navigation. CA1 neurons are some of the best characterized neurons available because the CA1 region is highly accesible for in vivo recording and easily delineated for slice electrophysiology, and much is known about its specific inputs and outputs. Imagine an Egyptian pyramid. Now imagine a giant tree growing up through the center of it to about 10 times its height. That is what a pyramidal neuron looks like. The roots of the tree are basilar dendrites and the branches are apical dendrites. Dendrites are specialized structures for receiving input. One giant root will run out of the bottom of the pyramid and send output to some downstream cell. This is the axon. One of the first things that Narayanan and Johnston showed was that the resonant frequency of a CA1 neuron varies along the apical extent of the dendritic tree. The frequency increases as you get further toward the top of the tree, from 3 Hz to 8 Hz at the top. This correlates with the quantity of the channels responsible for H-conductance which also increases toward the tippy-tops of the tree. Input into CA1 neurons is spatially organized such that the entorhinal cortex inputs at the very tip of the apical extent while the CA3 region of the hippocampus inputs at sites more proximal to the cell body. One hypothesis that the authors put forward is that the resonant properties may be tuned to the specific types of inputs. Unfortunately, I can't tell you whether entorhinal neurons fire at 8 Hz vs 3 Hz. I think this is an interesting avenue, but I wonder why you would need to filter the inputs by frequency if you already have them filtered by space. I suppose if the entorhinal cortex naturally fires around 8 Hz and you want the maximal downstream effect then its not so much a matter of filtering out bad frequencies as enhancing the good ones. The most interesting thing to me though was that certain excitation patterns could alter the resonant frequency. If, by direct stimulation, they caused the neuron to fire in bursts separated by about 100 ms, they could later observe a upward shift in the resonant frequency. They used several stimulation protocols. Of highest interest was the effect of inducing LTP. LTP (Long-Term Potentiation) is a cellular model for learning in memory. It involves the seleective strengthening of synapses between two coincidentally active neurons. There are various LTP inducing stimulation protocols. The one these folks used requires stimulating axons headed for the apical dendrites of the CA1 neuron while depolarizing the CA1 neuron's cell body to cause it to fire. Thus input activity is paired with downstream firing and that particular input is strengthened. Coincident firing is detected by a special receptor (the NMDA receptor) that is activated only when post-synaptic (dendritic, receiving end) membrane depolarization is paired with neurotransmitter release (from an axon of another neuron). After LTP induction, that input now has a bigger say in the overall activation election of the downstream neuron. The analogy between LTP and learning has been argued for decades now and some good evidence exists that this is a legitimate model. Early attempts to show this involved blocking the NMDA receptor in LTP and in learning and showing that both were impaired. Here is the key interesting thing for me about Narayanan and Johnston's paper. Blocking the NMDA receptor not only blocked LTP, but also blocked a global, non-input specific, upward shift in the resonant frequency of CA1 neurons. Now we have two physiological phenomena that you are manipulating when you inject an animal with an NMDA receptor antagonist. Is learning disrupted because of failed LTP or failed resonance shifts? Why would a resonance shift matter? Here's one reason. Neurons don't work alone. Thousands of neurons have to send input to one downstream neuron to get any reaction. They need to do this in a temporally coordinated fashion. One of the best methods for temporal coordination is oscillatory firing. Watch a tug of war sometime and note the effectiveness of "1,2,3 PULL!" compared to everybody struggling on their own time. This coordinated group of neurons is referred to as an ensemble. If members of the ensemble are connected to each other, they can settle on a frequency of oscillation that best excites everyone at once. If anyone gets out of line and starts going faster or slower, the big PULL will drag them back in, unless they are so far out that they simply can't get down with a certain tempo. If a CA1 neurons is part of some larger ensemble that really loves to fire at 3 Hz and then its resonant frequency jumps up to 5 Hz, it will be that much less responsive to its former buddies. Instead, some other more enticing fast-paced ensemble might recruit that dude into their little 5 Hz cult. The implication is that NMDA receptor-dependent learning could be caused by changes in ensemble size and strength rather than or in addition to strengthening or weakening of specific synapses. A good place to begin on testing this implication would be to record from CA1 neurons in live, behaving animals (this is routine) during a learning task and note whether their preferential firing pattern shifts in frequency and whether this is coordinated across multiple neurons. The H-conductance has more effects than just determining the resonant frequency. The Narayanan and Johnston paper was published alongside an article describing their effect on active properties of dendrites (dendritic calcium spikes) and third paper featuring the H-conductance prominently. Labels: CA1, LTP, Memory, Resonance |



