|
Thursday, March 05, 2009
Will information criteria replace p-values in common use? Some trends
posted by
agnostic @ 3/05/2009 12:30:00 AM
P-values come from null hypothesis testing, where you test how likely your observed data (and more extreme data) are under the assumption that the null hypothesis is true. As such, they do not allow us to decide which of a variety of hypotheses or models is true. The probability they encode refers to the observed data under an assumption -- it does not refer to the hypotheses on the table.
Using information criteria allows us to decide between a variety of hypotheses or models about how the world works. They formalize Occam's Razor by rewarding models that show a good fit to the observed data, while penalizing models that have lots of parameters to estimate (i.e., those that are more complex). Whichever one best balances this trade-off wins. Although I'm not a stats guy -- I'm much more at home cooking up models -- I've been told that the broader academic world is becoming increasingly hip to the idea of using information criteria, rather than insist on null hypothesis testing and reporting of p-values. So, let's see what JSTOR has to say. I did an advanced search of all articles for "p value" and for "Akaike Information Criterion" (the most popular one), looking at 5-year intervals just to save me some time and to smooth out the year-to-year variation. I start when the AIC is first mentioned. For the prevalence of each, I end in 2003, since there's typically a 5-year lag before articles end up in JSTOR, and estimating the prevalence requires a good guess about the population size. For the ratio of the size of one group to the other, I go up through 2008, since this ratio does not depend an accurate estimate of the total number of articles. From 2004 to 2008, there are 4132 articles with "p value" and 927 with "Akaike Infomration Criterion," so the estimate of the ratio isn't going to be bad even with fewer articles available during this time. Intervals are represented by their mid-point. Someone else can do the better job of searching year by year, perhaps restricting the search to social science journals to see if real headway is being made. (It would be uninteresting to see a rise of the popularity of information criteria in statistics journals.) Here are the trends in the use of each, as well as the ratio of p-value to AIC: 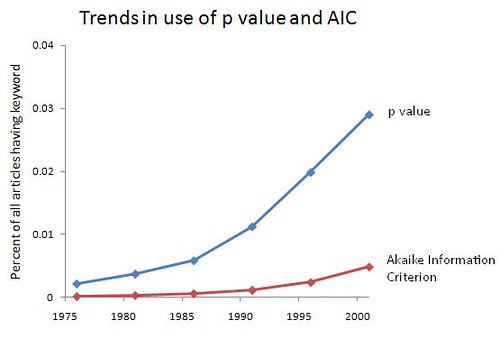  It's promising that both are increasing over the past 30-odd years, since that means more people are bothering to be quantitative. Still, less than 5% of articles mention p-values or information criteria -- some of that is due to the presence of arts and humanities journals, but there's still a big slice of the hard and soft sciences that needs to be converted. Also encouraging is the steady decline in the dominance of p-values to the AIC: they're still about 4.5 times as commonly used in academia at large, but that's down from about 15.5 times as common in the mid-1970s, a 71% decline. Graduate students and young professors -- the writing is on the wall. Aside from being intellectually superior, information criteria will give you a competitive edge in the job market, at least in the near future. After that, they will be required. Labels: academia, Modeling, Statistics
Tuesday, February 24, 2009
Male superiority at chess and science cannot be explained by statistical sampling arguments
posted by
agnostic @ 2/24/2009 05:37:00 PM
A new paper by Bilalic et al. (2009) (read the PDF here), tries to account for male superiority in chess by appealing to a statistical sampling argument: men make up a much larger fraction of chess players, and that the n highest extreme values -- say, the top ranked 100 players -- are expected to be greater in a large sample than in a small one. In fact, this explanation is only a rephrasing of the question -- why are men so much more likely to dedicate themselves to chess.
Moreover, data from other domains where men and women are equally represented in the sample, or where it's women who are overrepresented in the sample, do not support the hypothesis -- men continue to dominate, even when vastly underrepresented, in domains that rely on skills that males excel in compared to females. I show this with the example of fashion designers, where males are hardly present in the sample overall but thrive at the elite level. First, the authors review the data that male chess players really are better than female ones (p.2): For example: not a single woman has been world champion; only 1 per cent of Grandmasters, the best players in the world, are female; and there is only one woman among the best 100 players in the world. The authors then estimate the male superiority at rank n, from 1 to 100, using the entire sample's mean and s.d., and the fraction of the sample that is male and female. Here is how the real data compare to this expectation (p.2): Averaged over the 100 top players, the expected male superiority is 341 Elo points and the real one is 353 points. Therefore 96 per cent of the observed difference between male and female players can be attributed to a simple statistical fact -- the extreme values from a large sample are likely to be bigger than those from a small one. Therefore (p. 3): Once participation rates of men and women are controlled for, there is little left for biological, environmental, cultural or other factors to explain. This simple statistical fact is often overlooked by both laypeople and experts. Of course, this sampling argument doesn't explain anything -- it merely pushes the question back a level. Why are men 16 times more likely than women to compete in chess leagues? We are back to square one: maybe men are better at whatever skills chess tests, maybe men are more ambitious and competitive even when they're equally skilled as women, maybe men are pressured by society to go into chess and women away from it. Thus, the question staring us in the face has not been resolved at all, but merely written in a different color ink. The authors are no fools and go on to mention what I just said. They then review some of the arguments for and against the various explanations. But this means that their study does not test any of the hypotheses at all -- aside from rephrasing the problem, the only portion of their article that speaks to which answer may be correct is a two-paragraph literature review. For example, maybe females on average perform poorer on chess-related skills, and so weed themselves out more early on, in the same way that males under 6'3 would be more likely to move on and find more suitable hobbies than basketball, compared to males above 6'3. Here is the authors' response to this hypothesis (p. 3, my emphasis): Whatever the final resolution of these debates [on "gender differences in cognitive abilities"], there is little empirical evidence to support the hypothesis of differential drop-out rates between male and females. A recent study of 647 young chess players, matched for initial skill, age and initial activity found that drop-out rates for boys and girls were similar (Chabris & Glickman 2006). Well no shit -- they removed the effect of initial skill, and thus how well suited you are to the hobby with no preparation, and so presumably due to genetic or other biological factors. And they also removed the effect of initial activity, and thus how enthusiastic you are about the hobby. And when you control for initial height, muscle mass, and desire to compete, men under 6'3 are no more or less likely to drop out of basketball hobbies than men over 6'3. How stupid do these researchers think we are? So, this article really has little to say about the question of why men excel in chess or science, and it's baffling that it got published in the Proceedings of the Royal Society. The natural inference is that it was not chosen based on how well it could test various hypotheses -- whether pro or contra the Larry Summers ideas -- but in the hope that it would convince academics that there is really nothing to see here, so just move along and get home because your parents are probably worried sick about you. Now, let's pretend to do some real science here. The authors' hypothesis is that the pattern in chess or science can be accounted for by their statistical sampling argument -- but of course, men dominate all sorts of fields, including where they're about as equally represented in the pool of competitors, and even when they're outnumbered in that pool. Occam's Razor requires us to find a simple account of all these patterns, not postulating a separate one for each case. The simple explanation is that men excel in these fields due to underlying differences in genes, hormones, social pressures, or whatever. The statistical sampling argument can only capture one piece of the pattern -- male superiority where males make up more of the sample. Any of the non-sampling hypotheses, including the silly socio-cultural ones, at least are in the running for accounting for the big picture of male dominance regardless of their fraction of the sample. To provide some data, I direct you to an analysis I did three years ago of male vs. female fashion designers. Here, I'll consider "the sample of fashion designers" to be students at fashion schools since that's what the data were. Fashion students are the ones who will make up the pool of fashion designers upon graduating. I included four measures of eminence: 1) being chosen to enter the Council of Fashion Designers of America, 2) having an entry in two major fashion encyclopedias, both edited by women (Who's Who in Fashion, and The Encyclopedia of Clothing and Fashion), 3) having their collections listed on Vogue's website, and 4) winning the highest award of the CFDA, the Perry Ellis awards for emerging talent. The male : female ratio in the pool of fashion students is 1 : 13 at Parsons and 1 : 5.7 at FIT. So, the female majority in the sample of fashion designers is not quite as extreme as that of males in chess leagues, but pretty close. The statistical sampling argument predicts that females should out-number males at the top. But they don't -- the M : F ratios for the four measures above are, respectively, 1.29 : 1, 1.5 : 1 and 1.9 : 1, 1.8 : 1, and 3.6 : 1. Again, this isn't as extreme as male superiority in chess, but recall that males are so underrepresented in the sample to begin with! (For other design fields that males tend to have greater interest in, such as architecture, the M : F ratios among the winners of the Pritzker Prize and the AIA Gold Medal are, respectively, 27 : 1 and 61 : 0). The authors statistical sampling argument is not a null hypothesis that we reject or fail to reject in any particular case -- rejecting it in fashion design, and failing to reject in chess. It is not a hypothesis at all, but simply a rephrasing of the observation that men dominate certain fields, only measuring this by their greater participation rates. Again, it does not address why males are so much more likely to participate in chess leagues to begin with, which could be due to any of the existing hypotheses about male superiority. The point is that it is a widespread phenomenon that requires a single explanation applying across domains. I find the genetic and hormonal influences on the mean and variance of cognitive ability and personality traits to be the most promising (just search our archives for relevant keywords to find the discussions). But this study of chess players offers nothing new to the debate, and could not do so even in principle, as it doesn't make a novel hypothesis, apply a novel test to existing data, or apply existing tests on novel data. You can reformulate the observation or problem however you please, but that doesn't make the testing of hypotheses go away. Reference: Bilalic, Smallbone, McLeod, and Gobet (2009). Why are (the best) Women so Good at Chess? Participation Rates and Gender Differences in Intellectual Domains. Proc. R. Soc. B, 276, 1161–1165. Labels: Larry Summers, psychometric smoke and mirrors, sex differences, Statistics
Sunday, November 25, 2007
Linguist: I can use R, you can't. Thus, your motives are questionable. QED.
posted by
p-ter @ 11/25/2007 09:18:00 AM
Mark Liberman at Language Log (a blog which I very much enjoy, I should point out) approvingly links to Cosma Shalizi's rant against Slate for publishing a series of articles on race and IQ. His conclusion:
So to start with, you should ask yourself whether you can define and calculate the variance of a set of numbers, or the correlation between two sequenccs of numbers. If not, then read the (linked) wikipedia articles -- and spend a little time playing with the concepts in the context of an interactive program like R. Once you've paid that entry fee, read Cosma's posts. (It's more fun that you might think -- I especially recommend the discussion of the heritability of zip codes, and you could go back and read the prequel about the heritability of accent.) And then go through William Saletan's articles, and decide for yourself what they mean about the abilities and motivations of the writer and his editors.It's amazing how quickly people go from simple disagreement to armchair psychologist mode; a little perspective is in order here. Dr. Liberman assumes that Cosma concludes that heritability estimates are worthless. This is not the case. Cosma points out that estimating heritability involves making assumptions that are often incorrect, but (I feel like I've said this many times before) all models are wrong, but some are useful. And buried in his prose (which contains many important, ill-understood points about the estimation of heritability), he cites a nice paper on the heritability of IQ, which concludes for a narrow-sense heritability of ~0.34 (that is, additive genetic factors account for ~34% of the variance in IQ, see the linked post). Cosma wants to add additional parameters to this model before he makes any definitive statements, but he can't bring himself to treat IQ differently than other traits: If you put a gun to my head and asked me to guess [whether there are genetic variants that contribute to IQ], and I couldn't tell what answer you wanted to hear, I'd say that my suspicion is that there are, mostly on the strength of analogy to other areas of biology where we know much more. I would then - cautiously, because you have a gun to my head - suggest that you read, say, Dobzhansky on the distinction between "human equality" and "genetic identity", and ask why it is so important to you that IQ be heritable and unchangeable.So if he had to guess, there is probably a genetic component to IQ, environment also plays a role, and human equality is not dependent on genetic identity. Seriously, read Saletan's column--these are exactly his points! Referring back to my point about the utility of incorrect models, it's worth noting that, if you don't accept any of the heritability estimates proposed in humans, you're rejecting that any trait could be determined to have a genetic component before, oh, 2001. I don't think that's a good idea, and here's why: the heritability of type II diabetes was estimated at a "mere" 0.25 (using all those horribly flawed methods, and including, since it is a dichotomous trait, even more assumptions); now molecular studies have identified at least 9 loci involved in the disease. The heritability of Type I diabetes was estimated at about 0.88; now, there are 10 loci undoubtably associated with the disease. There are other examples, and more sure to come, but suffice it to say that heritability studies, with all their seemingly ridiculous assumptions, are not worthless. Now look to Cosma's post on g. Again, this time in the footnotes, we see something in line with Saletan's article. Referring to the observation by economist Tyler Cowen that some people he knew in a village in Mexico were smart in ways not measureable by IQ tests, he writes: Cowen points out behaviors which call for intelligence, in the ordinary meaning of the word, and that these intelligent people would score badly on IQ tests. A reasonable counter-argument would be something like: "It's true that 'intelligence', in the ordinary sense, is a very broad and imprecise concept, and it's not surprising the tests don't capture it perfectly. But the aspects of 'intelligence' they do capture are ones which are vastly more important for economic development than the ones displayed by Cowen's friends in San Agustin Oapan, however amiable or even admirable those traits might be in their own right." This would be a position about which one could have a rational argument. (Indeed, I might even agree with that statement, as far as it goes, as might A. R. Luria.)So Cosma "might" agree that intelligence, as operationally defined by psychologists, is important for economic development and differs in distribution between groups. Interesting. Cosma's posts seem to follow any discussion of IQ around in the "blogosphere". They're well-written, include legitimate discussion of many important issues in quantitative genetics and IQ testing (ok, I don't know much about IQ testing, but I'm assured this is the case by people who do), and come from an authority. But for whatever reason (I'm tempted to think that people don't actually read what he writes. I mean, it has, like, math and stuff), he's interpreted as saying that intelligence tests and the concept of heritability are entirely meaningless. That is not the case. Labels: Genetics, IQ, Statistics
Monday, November 12, 2007
In an interesting story on the relationship between teen delinquency and sex (long story short: people who concluded early sex caused delinquency unsurprisingly failed to control for genetics and were led astray) I saw this little bit:
A recent study by Scottish researchers asked whether the higher IQs seen in breast-fed children are the result of the breast milk they got or some other factor. By comparing the IQs of sibling pairs in which one was breast-fed and the other not, it found that breast milk is irrelevant to IQ and that the mother's IQ explains both the decision to breast-feed and her children's IQ.Now, this is interesting in light of the recent study claiming to find a gene-environment interaction between breast-feeding and a particular gene. The source for the claim that breast-feeding has no effect on IQ is here. I went back and looked at the recent paper's attempts at controlling for maternal IQ. Statstically, this is not a difficult thing to do-- a linear regression of child IQ on maternal IQ, breast feeding status and genotype can easily be compared with a model that includes a breast feeding staus X genotype interaction. The authors don't do this standard analysis, however--they only include a cryptic note explaining that there is no significant "interaction" between the SNP in question and maternal IQ. It's not the interaction term that's interesting, of course; it's whether the marginal effect of maternal IQ removes their already tenuous claims of an interaction between breast feeding and genotype. One gets the distinct feeling that some unfavorable results are being swept under the rug. Combine this, plus the study above, then add your prior probability that by genotyping two (2!) SNPs in the entire genome you'll find a real gene-environment interaction, and, well, it's not a stretch to say the authors haven't quite demonstrated what they think they have. Labels: Genetics, IQ, Statistics
Tuesday, March 06, 2007
 A new paper in PNAS (open access) uses DNA isolated from seized ivory to investigate where elephant poaching is occurring. It's an interesting idea, but for me the idea itself takes a back seat to the clever statistical framework in which it's implemented. The analysis of DNA data is getting more and more sophisticated; this is an excellent example of that phenomenon. A new paper in PNAS (open access) uses DNA isolated from seized ivory to investigate where elephant poaching is occurring. It's an interesting idea, but for me the idea itself takes a back seat to the clever statistical framework in which it's implemented. The analysis of DNA data is getting more and more sophisticated; this is an excellent example of that phenomenon. The paper starts with very little data-- 37 tusks from this ivory seizure along with a database of DNA samples of elephants from all over Africa. Traditional methods would treat each of the 37 tusks independently, but the authors want to consider the possibliity that all came from a single area as well as the possiblity that all are from disparate parts of the continent (the two possiblities have different implications for law enforcement). So they create a grid on all of Africa (actually, just the subset containing the elephant range) and randomly split the grid into polygons, considering each polygon as equally likely to be part of area where elephants were poached. This gives them a prior distribution for the origin of the poached elephants. They then use their data and the existing database to estimate the posterior distribution for that origin using Markov chain Monte Carlo. They provide evidence that this method works very well at distinguishing the two possiblities (a single origin of the elephants or a disparate collection), an advertisement for Bayseian methods and their ability to get as much information as possible from limited data. As can be seen in the figure, all the elephants seem to come from an area centered around Zambia. This has had some consequences: The seizure immediately followed Zambia's application to CITES for a one-off sale of their ivory stockpiles at COP12 (Conference of the Parties). That application maintained that only 135 elephants were known to have been illegally killed in Zambia during the previous 10 years, woefully shy of the 3,000-6,500 elephants we estimate to have been killed in Zambia surrounding the seizure, let alone during that entire 10-year period. Subsequent to being informed of our findings, the Zambian government replaced its director of wildlife and began imposing significantly harsher sentences for convicted ivory traffickers in its courts. Labels: Genetics, Statistics
Tuesday, February 27, 2007
One of the more heated debates in human medical genetics in the last decade or so has been centered around the Common Disease-Common Variant (CDCV) hypothesis. As the name implies, the hypothesis posits that genetic susceptibility to common diseases like hypertension and diabetes is largely due to alleles which have moderate frequency in the population. The competing hypothesis, also cleverly named, is the Common Disease-Rare Variant (CDRV) hypothesis, which suggests that multiple rare variants underlie susceptibility to such diseases. As different techniques must be used to find common versus rare alleles, this debate would seem to have major implications for the field. Indeed, the major proponents of the CDCV hypothesis were the movers and shakers beind the HapMap, a resource for the design of large-scale association studies (which are effective at finding common variants, much less so for rare variants).
However, CDCV versus CDRV is an utterly false dichotomy, as I'll explain below. This point has slipped past many of the human geneticists who actually do the work of mapping disease genes, and I feel the problem is this: essentially, geneticists are looking for a gene or the gene, so they naturally want to know whether to take an approach that will be the best for finding common variants or one for finding rare variants. However, common diseases do not follow simple Mendelian patterns-- there are multiple genes that influence these traits, and the frequencies of these alleles has a distribution. A decent null hypothesis, then, is to assume that the the frequencies of alleles underlying a complex phenotype is essentially the same as the overall distribution of allele frequencies in the population-- that is, many rare variants and some common variants. This argument would seem to favor the CDRV hypothesis. Not so. The key concept for explaining why is one borrowed from epidemiology called the population attributable risk--essentially, the number of cases in a population that can be attributed to a given risk factor. An example: imgaine smoking cigarettes gives you a 5% chance of developing lung cancer, while working in an asbestos factory gives you a 70% chance. You might argue that working in an asbestos factory is a more important risk factor than cigarette smoking, and you would be correct--on an individual level. On a population level, though, you have to take into account the fact that millions more people smoke than work in asbestos factories. If everyone stopped smoking tomorrow, the number of lung cancer cases would drop precipitously. But if all asbestos factory workers quit tomorrow, the effect on the population level of lung cancer would be minimal. So you can see where I'm going with this: common susceptibility alleles contribute disproportinately to the population attributable risk for a disease. In type II diabetes, for example, a single variant with a rather small effect but a moderate frequency accounts for 21% of all cases[cite]. So am I then arguing in favor of the CDCV hypotheis? Of course not-- rare variants, aside from being predictive for disease in some individuals, also give important insight into the biology of the disease. But it is possible right now, using genome-wide SNP arrays and databases like the HapMap, to search the entire genome for common variants that contribute to disease. This is an essential step--finding the alleles that contribute disproportionately to the population-level risk for a disease. Eventually, the cost of sequencing will drop to a point where rare variants can also be assayed on a genome-wide, high-throughput scale, but that's not the case yet. Once it is, expect the CDRV hypothesis to be trumpted as right all along. Labels: Association, disease, Genetics, Statistics |



