|
Friday, November 30, 2007
A few months ago, I pointed out a paper identifying variants near the FTO gene as being involved in obesity. I noted how strikingly little was known about this gene, concluding:
So essentially, nothing is known about this gene. Thanks to this study, this is unlikely to be the case for long.Little did I know it would only take a few months to get the ball rolling! From this week's Science: Variants in the FTO (fat mass and obesity associated) gene are associated with increased body mass index in humans. Here, we show by bioinformatics analysis that FTO shares sequence motifs with Fe(II)- and 2-oxoglutarate–dependent oxygenases. We find that recombinant murine Fto catalyzes the Fe(II)- and 2OG-dependent demethylation of 3-methylthymine in single-stranded DNA, with concomitant production of succinate, formaldehyde, and carbon dioxide. Consistent with a potential role in nucleic acid demethylation, Fto localizes to the nucleus in transfected cells. Studies of wild-type mice indicate that Fto messenger RNA (mRNA) is most abundant in the brain, particularly in hypothalamic nuclei governing energy balance...This is an absolutely beautiful example of the hypothesis-generating power of genome-wide association studies. Studying the genetic variation underlying a trait is simply a great way to get at the mechanism by which the trait works. This point is lost on many people--even if the "environment", however you want to define it, plays the most important role in a trait (like it may in obesity, for example), there are an infinite number of hypotheses about which environmental variables might be relevant, and once you find a correlation, it's both difficult to establish causality and you get very little information about the mechanism by which the trait works (yes, eating a lot leads to increased weight in most people, but how?). In genetics, there is a finite number of hypotheses (there are many millions of genetic variants in humans, and all of them will eventually be testable), the road to establishing causality is much clearer (ie. this genetic variant leads to increased probability of obesity--it would be difficult to argue the inverse), and you immediately have your foot in the door to study the molecules involved in the trait. Again, this is a wonderful example of all of these points. Labels: Genetics
Happy 100 years Jacques Barzun!!!! Check out Jacques Barzun Centennial for a list of resources.
Wednesday, November 28, 2007
I have previously reported on the annual education statistics in Britain (e.g. here), so I will give an update for 2006-07. Figures have just been published for performance at the GCSE examinations, taken by most children at age 16. An official press release is here. Performance by children of all ethnic groups continues to improve (as measured by examination grades). The press release highlights the fact that the gap between ethnic groups is narrowing. Actually, this is not strictly true. The 'narrowing' is specifically between children of Black (Caribbean or African) origin and the (mainly White) average. Other 'gaps' are constant or widening. Children of Pakistani origin have the lowest rate of improvement, and have now been overtaken by Black Africans.
I won't discuss the vexed question whether improvement in examination results actually indicates any improvement in education. But I guess (unless anyone knows reasons to the contrary) that the changes in differentials between ethnic groups are real and not artificial; for example, I can't see any reason why the testing system should be biased against Pakistanis but not Bangladeshis. Added on 1 December: In comments the point has been made that a general rising trend will tend to suppress differentials. In general this is a good point, but as I mentioned in my original post, not all of the gaps are narrowing. The pattern is more complex. Also, the (mainly White) average is still nowhere near the ceiling. It has also been suggested that the narrowing gap between Black African and Black Caribbean and White children could be due to increasing proportions of mixed-race children. This should not be the case. The statistics classify the various mixed-race groups separately, so provided the children are correctly classified this should not be a problem. Finally, I should warn against taking these results as indicators of IQ. No doubt there is some correlation with IQ, but it can hardly be very close, as girls have much better GCSE results than boys despite similar IQ. I would suggest that before making further comments readers should consult the original statistics. Go here, click on the link marked 'EXCEL', then go to Table 8 for the GCSE figures. (If you don't have an Excel reader there are free downloads on the web.)
Tuesday, November 27, 2007
Mark Liberman has updated his post on race and IQ in response to my post. I actually wrote out a long response and deleted it--believe it or not, I have about as much of a desire to get sucked into this conversation as he does. But I strongly, strongly disagree with his claim that showing two populations have different distributions of IQ and claiming genetics plays a role is, in itself, a "racist theory". My point in the post was that the basic premises of Saletan's article (ie. that there are aspects of "intelligence" that are socially relevant, probably have a genetic component, and differ in distribution across populations) are entirely accepted by Shalizi (ok, he "might agree" with them). This is because they're obvious in the light of evolutionary theory (allele frequencies evolve by natural selection and genetic drift. This includes alleles involved in socially awkward phenotypes like IQ). I'm not opposed to people holding out for more evidence, but imputing nefarious motives to writers for talking about the evidence that exists I do find questionable.
Sunday, November 25, 2007
 We have already seen that female adult film stars are just average in height, while sexy celebrities are a half-sigma above-average. However, consider the heights of the 2007 Miss World contestants, whose median is 68.9 in (N = 106), a clearly significant difference from the US mean of 64.1 in. (where an SD = 3 in.), let alone the mean height of the second and third-world countries that most of the contestants come from. And though I can't find the original cite, many websites quote the Association of Modeling Agents as saying that female models should be at least 5'8. So, if tall women are not more attractive physically, as the first two data-sets suggest, but are more glamorous or prestigious, as the latter two suggest, there is a simple account of all of the data. We have already seen that female adult film stars are just average in height, while sexy celebrities are a half-sigma above-average. However, consider the heights of the 2007 Miss World contestants, whose median is 68.9 in (N = 106), a clearly significant difference from the US mean of 64.1 in. (where an SD = 3 in.), let alone the mean height of the second and third-world countries that most of the contestants come from. And though I can't find the original cite, many websites quote the Association of Modeling Agents as saying that female models should be at least 5'8. So, if tall women are not more attractive physically, as the first two data-sets suggest, but are more glamorous or prestigious, as the latter two suggest, there is a simple account of all of the data.First, it's worth reviewing a few key facts about tall women and successful men, which come from Jensen & Sinha's (1993) excellent review of the physical correlates of intelligence. There is a positive correlation between height and IQ of roughly 0.2 -- however, all of this is due to between-family differences, as there is no within-family differences. In other words, while members of tall families tend to be smart, within a given family, there is no relationship between height and IQ. Therefore, we can rule out some genetic causes such as pleiotropy, where a gene has effects on more than one trait; and genetic linkage, where genes for height may lie close to genes for IQ and be pulled along with them like teammates in a game of Red Rover. Common environmental causes like nutrition do not likely account for the pattern since most of the data comes from first-world populations not subject to much environmental stress, and also because the height-IQ correlation holds even among those with gifted IQs, who do no inhabit slums or want for basic nutrients. Interestingly, the height-IQ correlation is entirely due to differences in leg length, since the correlation vanishes when sitting height is used instead of standing height. The simplest explanation that Jensen & Sinha propose is that there is cross-assortative mating between female leg length and male IQ. They summarize several studies which show that tall women, no matter what economic class they are born into, tend to climb the economic ladder more easily and marry higher-status husbands. That pools tall and smart genes into the same family, but any given kid of theirs doesn't get to pick and choose which parent he gets his height or IQ genes from, which explains why height and IQ are uncorrelated within families. Moreover, this is not a pattern only among the rich and bright: at every level of IQ, the pattern holds. Jensen & Sinha suggest that men find tall women physically more attractive, and they mention the heights of Miss Universe contestants as support. But as we've seen, beauty pageant contestants and runway models are an entirely different group from adult film stars and sexy celebrities, who more accurately reflect what males find physically attractive. Therefore, to the extent that tall women are preferred as mates, it is probably so that the man can show her off as a hard-to-acquire status symbol, like a Porsche. This is an honest signal of high status since you don't have to conduct studies to know that a guy with a tall wife is far more likely to be a somebody than a nobody. That's especially true when the woman is not just tall, but taller than her mate, as shown in this gallery of famous shorter man / taller woman couples. We leave aside what makes a man high-status -- it could include wealth, power independent of wealth (as with Dennis Kucinich), and so on. Broadcasting his status in this way might allow him to attract the attention of a large number of attractive onlooking females, who he may then seek on-the-sly copulations with. It may also allow him to be taken more seriously by his male colleagues and inferiors, and so to rise further in status: "Hey, that guy has a 6' tall wife -- he must be a real go-getter." Both of these effects serve to increase his reproductive fitness. And importantly, parading around your tall wife is a far less vulgar signal of status than, for example, driving up in an obscenely expensive car or sporting tons of jewelry. Consequently, the man does not suffer a loss of reputation as he would with those other signals, and because it is less conspicuous, he is less likely to draw the ire of those around him. He will provoke class envy in them, for sure, but he has to be careful not to enrage or offend them either, since social politics are central to his status. Finally, because height is highly heritable, he may seek a taller wife more as a long-term wife than a short-term fling since he is concerned about the upward mobility of the children who he invests in. Mating with a tall woman will give his kids a leg up in the status competition. In the case of on-the-sly mating, he will not invest much in them later on, so he could be less worried about their social mobility -- just have a lot of them and hope some do well. Reference: Jensen, A. & S. Sinha (1993). Physical correlates of human intelligence. In P. Vernon (Ed.), Biological approaches to the study of human intelligence, pp. 139-242. Labels: babes and hunks, height, reproductive strategies, status
Linguist: I can use R, you can't. Thus, your motives are questionable. QED.
posted by
p-ter @ 11/25/2007 09:18:00 AM
Mark Liberman at Language Log (a blog which I very much enjoy, I should point out) approvingly links to Cosma Shalizi's rant against Slate for publishing a series of articles on race and IQ. His conclusion:
So to start with, you should ask yourself whether you can define and calculate the variance of a set of numbers, or the correlation between two sequenccs of numbers. If not, then read the (linked) wikipedia articles -- and spend a little time playing with the concepts in the context of an interactive program like R. Once you've paid that entry fee, read Cosma's posts. (It's more fun that you might think -- I especially recommend the discussion of the heritability of zip codes, and you could go back and read the prequel about the heritability of accent.) And then go through William Saletan's articles, and decide for yourself what they mean about the abilities and motivations of the writer and his editors.It's amazing how quickly people go from simple disagreement to armchair psychologist mode; a little perspective is in order here. Dr. Liberman assumes that Cosma concludes that heritability estimates are worthless. This is not the case. Cosma points out that estimating heritability involves making assumptions that are often incorrect, but (I feel like I've said this many times before) all models are wrong, but some are useful. And buried in his prose (which contains many important, ill-understood points about the estimation of heritability), he cites a nice paper on the heritability of IQ, which concludes for a narrow-sense heritability of ~0.34 (that is, additive genetic factors account for ~34% of the variance in IQ, see the linked post). Cosma wants to add additional parameters to this model before he makes any definitive statements, but he can't bring himself to treat IQ differently than other traits: If you put a gun to my head and asked me to guess [whether there are genetic variants that contribute to IQ], and I couldn't tell what answer you wanted to hear, I'd say that my suspicion is that there are, mostly on the strength of analogy to other areas of biology where we know much more. I would then - cautiously, because you have a gun to my head - suggest that you read, say, Dobzhansky on the distinction between "human equality" and "genetic identity", and ask why it is so important to you that IQ be heritable and unchangeable.So if he had to guess, there is probably a genetic component to IQ, environment also plays a role, and human equality is not dependent on genetic identity. Seriously, read Saletan's column--these are exactly his points! Referring back to my point about the utility of incorrect models, it's worth noting that, if you don't accept any of the heritability estimates proposed in humans, you're rejecting that any trait could be determined to have a genetic component before, oh, 2001. I don't think that's a good idea, and here's why: the heritability of type II diabetes was estimated at a "mere" 0.25 (using all those horribly flawed methods, and including, since it is a dichotomous trait, even more assumptions); now molecular studies have identified at least 9 loci involved in the disease. The heritability of Type I diabetes was estimated at about 0.88; now, there are 10 loci undoubtably associated with the disease. There are other examples, and more sure to come, but suffice it to say that heritability studies, with all their seemingly ridiculous assumptions, are not worthless. Now look to Cosma's post on g. Again, this time in the footnotes, we see something in line with Saletan's article. Referring to the observation by economist Tyler Cowen that some people he knew in a village in Mexico were smart in ways not measureable by IQ tests, he writes: Cowen points out behaviors which call for intelligence, in the ordinary meaning of the word, and that these intelligent people would score badly on IQ tests. A reasonable counter-argument would be something like: "It's true that 'intelligence', in the ordinary sense, is a very broad and imprecise concept, and it's not surprising the tests don't capture it perfectly. But the aspects of 'intelligence' they do capture are ones which are vastly more important for economic development than the ones displayed by Cowen's friends in San Agustin Oapan, however amiable or even admirable those traits might be in their own right." This would be a position about which one could have a rational argument. (Indeed, I might even agree with that statement, as far as it goes, as might A. R. Luria.)So Cosma "might" agree that intelligence, as operationally defined by psychologists, is important for economic development and differs in distribution between groups. Interesting. Cosma's posts seem to follow any discussion of IQ around in the "blogosphere". They're well-written, include legitimate discussion of many important issues in quantitative genetics and IQ testing (ok, I don't know much about IQ testing, but I'm assured this is the case by people who do), and come from an authority. But for whatever reason (I'm tempted to think that people don't actually read what he writes. I mean, it has, like, math and stuff), he's interpreted as saying that intelligence tests and the concept of heritability are entirely meaningless. That is not the case. Labels: Genetics, IQ, Statistics
As a follow-up on a previous post about the heights of female sex symbols picked from the pool of celebrities, which found that they're about 1/2 SD above-average, let's now look at how tall adult film stars are. They're worth examining since they are chosen almost exclusively based on how attractive they are to the average male consumer, not how elegant or confident they appear. The website of the modeling agency that hosts the more elite stars -- LA Direct Models (NSFW) -- has height data for all but a couple of their members. If anything, these data are probably biased toward taller height since everyone lies in the upward direction.
Here is the frequency distribution of this sample of 121: The mean is 64.5 in., the SD is 2.6 in., and the skewness is 0.24, which indicates it is weakly positively skewed (more of the points are bunch around the lower end). In a representative sample of the general population (see this PDF, p.10), females aged 20-29 have a mean height of 64.1 in. Because the adult film star sample could easily by biased by a half-inch, and because the means are close enough anyway, I won't bother running a t-test. If you really want to, feel free to post it in the comments, but it's clear that the adult film stars are not taller or shorter than the population at large. Because the females are chosen only based on how physically attractive they are, this result goes against the hypothesis that long legs are in general physically attractive to men (although some men may find them sexy). There is another, non-physical reason why tall women may be preferred as mates, which I'll post about soon. Labels: babes and hunks, height, maintenance of variation
Friday, November 23, 2007
Reading the Bhagavad Gita I am struck (as usual) by commonalities between mystical philosophies rooted in a method of psychological introspection and meditation. For example, the tendency toward monism is marked across many traditions which emerge out of specific religious or philosophical movements. This even includes the monotheistic religions of the West, whose creeds and beliefs tend to notionally reject monism and imply the separation of a personal God from his Creation. The Perennial Philosphy emergred from this empirical observation of the relatively uniform experience of mystics, and the field of Religious Studies has been influenced this idea, in particular through the work of Mircea Eliade. Eliade and his fellow travelers conceive of religious experience as a window into a sacred reality, distinct from the profane world. Obviously, I don't believe this. Rather, I am struck by the fact that very few mystics ever report that they have looked upon the 6
3 essences of the universe. Or any specific deviation from the One. Rather, mystical trance seems to blur distinctions across categories as all perception melts into a unitary underlying essence, whether you call it God or the One. In contrast to mysticism theology tends to explore a huge sample space of possibilities and configurations. Why is this? I suspect it is because theology tends to rely on explicit chains of inferences based on verbal logic, and quite often individuals may differ in their sense of what is implied by a particular proposition. In contrast, the heightened consciousness of mysticism and the sense of the One is probably reflecting underlying neurological realities. The One isn't the real nature of the universe, it is simply the common output the brain pops out when put under the ascetic stresses or mental techniques which mystics utilize to change their consciousness. I am generally skeptical of neurotheology when it claims to explain religion, but I do believe it is on its way to accurately sketching out the shape of mysticism (obviously it doesn't explain religion because I think that mysticism is simply a subset of religion, not the totality of it). Labels: Religion
Thursday, November 22, 2007
Research in the latest issue of Nature provides evidence that babies can distinguish 'helpful' from 'unhelpful' people at a very early age, before they acquire language and (presumably) before they can have learned the distinction from their own experience. The evidence comes from staged scenarios using 'nice' and 'nasty' dolls. Babies prefer the nice ones. The researchers argue that this must be an evolved adaptation for social living, which seems plausible enough. Someone should try the same experiment with chimps and other primates. To understand the evolution of morality (in my opinion) we need more good experiments and less mathematical theorising, or at least a better balance between the two.
Here is a report from today's London Times. No doubt there are others. Added: I assume, though it is not clear from the Times report, that the researchers have excluded the possibility that babies just prefer triangles to squares.
In a few recent posts I've referred to the fact that variation on the OCA2 locus can predict about 3/4 of the eye color variation in the European population. Specifically, OCA2 is probably the quasi-Mendelian locus which is the culprit behind the classical dominant/recessive pedigree inheritance patterns which geneticists have long noted. The genomic region has also been subjected to a recent selection event. Why?
One model posits that the selection is directly for blue eyes. For example, some sort of sexual selection where blue eyes are strongly preferred. There's a problem with any model which posits selection for blue eyes: at very low frequencies selection on recessive traits is weak. That is, if you have alleles responsible for blue eyes extant at a frequency of 10%, only 1% of the population will express blue eyes (assumes random mating and a tighter correlation between the alleles and the phenotype as well as perfect dominance/recessiveness, all violated, but gets the logic across). So only 1 out of 10 blue eye causing alleles can be subject to selection. A way to get around this issue is population substructure, imagine that you have small demes drifting in all directions. A deme which drifts to a high or fixed frequency of blue eyes can then allow selection to operate strongly upon the allele responsible for this trait. This also requires specific meta-population dynamics so as to prevent these high frequency demes from being swamped out by gene flow from low frequency demes. Frankly, I'm really skeptical that a continent wide Shifting Balance process can really explain the third longest haplotype in the European genome. But there's another model, a bit simpler: the gene responsible for blue eyes is being selected for a another reason. Blue eyes are simply a byproduct, and that other reason is additive in its phenotypic expression so that even single copy variants are subject to the power of selection. I would hazard to guess that the most boring explanation here would be skin color. I've offered below that OCA2 does track skin color variation, but I've been pretty vague about this. The data isn't always easy to find, so I've repackaged Table 5 from A Three-Single-Nucleotide Polymorphism Haplotype in Intron 1 of OCA2 Explains Most Human Eye-Color Variation. Please note that there is a typo in the table in the paper, they have the correct data in the text, so I went by that.
Obviously there are other genes at work in regards to skin color, there's some population substructure which is probably lurking in the data, and the association of the variants themselves with an eye color aren't perfect either. That being said, this isn't the only study which does note that OCA2 has not only localized affects, but some global affects as well. Labels: Genetics, Pigmentation
Wednesday, November 21, 2007
Season of Birth and Dopamine Receptor Gene Associations with Impulsivity, Sensation Seeking and Reproductive Behaviors.
Labels: Genetics
Tuesday, November 20, 2007
Reading the links that come in to GNXP, I happened upon this post on what the author referrs to as "scientific racism". This bit caught my eye:
I sat on a grant review committee recently for a national-level competition for multi-million dollar grants of an agency I won't name. The review committee was quite large, probably 25 or more scholars from around the U.S. One of the grant applications that the other reviewers (mostly from the biological sciences) rated the highest was one that proposed to look at the "genetic racial differences among Blacks and whites" to different kinds of treatment for HIV/AIDS. I rated this grant proposal among the lowest I had reviewed because of the methodology: all of the participants in the study would be sorted into the supposedly self-evident categories "Black" and "white" based on self-identification. When I raised this objection among my colleagues in the biological and health sciences, they all blinked hard, and looked at me as if I'd committed some sort of unpleasant faux pas. The chair of the committee finally acquiesced that this was a methodological flaw in the proposal, but the grant was nevertheless awarded millions of dollars.Biomedical researchers are caught between a rock and a hard place here--none of them enjoy being referred to as scientific racists by their colleagues, I'm sure, but they're also interested in real phenomena. It's well-known that minorities are less likely to participate in biomedical research (though recent studies suggest this is not because they're less willing). From a geneticist's perspective, the discomfiting implication of this is that tests of a drug's efficacy and safety are done on a range of genetic backgrounds that are strongly biased towards the European mean. That is, drugs are accepted or rejected largely based on how well they perform in a sample of individuals of European descent. This is obviously a problem for the applicability of any results, and the NIH is indeed making minority inclusion a requirement for funding certain projects. Clearly, none of this would be an issue if everyone responded identically to drugs (or if the correlation between drug response and race were zero). It is, however, an issue. Now, ancestry could be related to drug response through any number of mechanisms, either directly (through genetics) or indirectly (through socioeconomic status, etc). Teasing apart those influences means looking at both of them. But then you have someone like the author, who simply dismisses the correlation altogether! And who evidently has some say in the funding of these studies! It's worth pointing out that HIV progression does indeed have a genetic component and that certain alleles like CCR5-delta32, which is strongly protective against HIV infection, show marked geographic differences in frequency. A priori, looking for genetic components to differential drug response between populations seems entirely reasonable. Lastly, her main point seems to be that genetic ancestry and self-identified race might not match up. They do. I'm well-aware that positions like the author's are made possible by people at the other end of the spectrum, who see races as the embodiment of some Platonic ideal. But rejecting idiocy certainly does not require one to embrace blindness! Related: Cancer and Race
Peter Frost states:
I suspect there is some incipient sex-linkage, i.e., European women may be somewhat likelier to have non-brown eyes and non-black hair. If this sex-linkage is mediated by prenatal estrogenization there may also be some impact on personality and temperament. But I really don’t know, and unfortunately there are still more questions than answers.  I've read Peter's book, Fair Women, Dark men, and it is a great collection of data. Also, he has theorized that European color variation is a byproduct of selection selection. So I have been primed to look for a trend where women seem to express blondism or light eye color at higher frequencies. But I just haven't found anything like that. In fact, I've found data which goes in the other direction, that is, females have a higher frequency of brown eyes! But this really clinched it for me: I've read Peter's book, Fair Women, Dark men, and it is a great collection of data. Also, he has theorized that European color variation is a byproduct of selection selection. So I have been primed to look for a trend where women seem to express blondism or light eye color at higher frequencies. But I just haven't found anything like that. In fact, I've found data which goes in the other direction, that is, females have a higher frequency of brown eyes! But this really clinched it for me: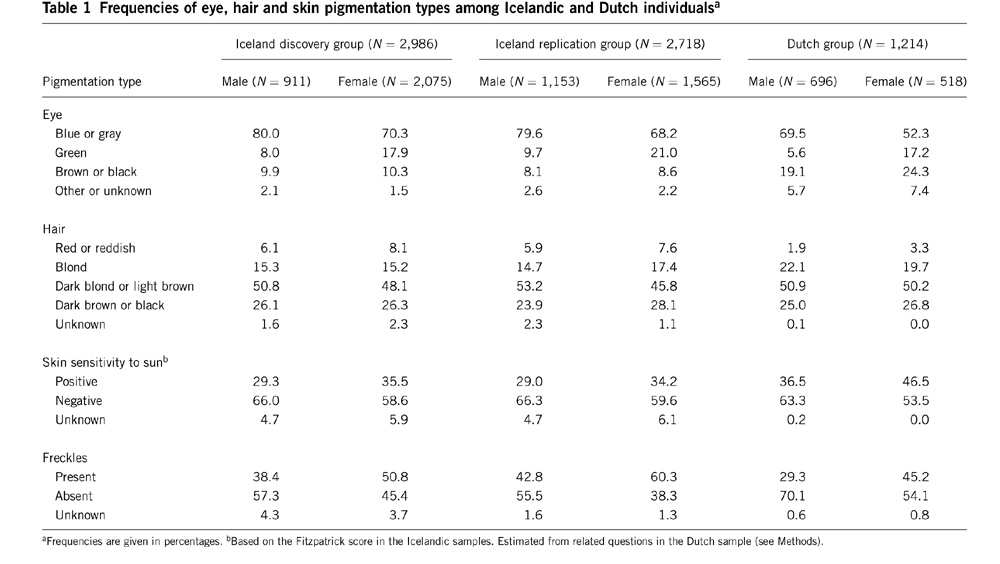 The source is this paper, Genetic determinants of hair, eye and skin pigmentation in Europeans. Note that women tend to score higher on skin sensitivity toward sun, which implies that they do have ligher skin. And as for hair color, well, perhaps there is a difference in how one judges blonde vs. brunette for males and females? I don't know. But the eye color data I've seen elsewhere and just dismissed it as small N or something like that. At this point my assumption is that there isn't really the sexual dimorphism in eye color that there is most definitely is in skin color. As for hair, I'm more open to this since it seems that it is subject to more genes, and there could be some hormonal factor as the tendency toward greater blondism in children and females is noted among Australian Aboriginals as well. Anyway, forget visual inspection. Here's the associations taking sex into account (from Table 4 of supplementary info): 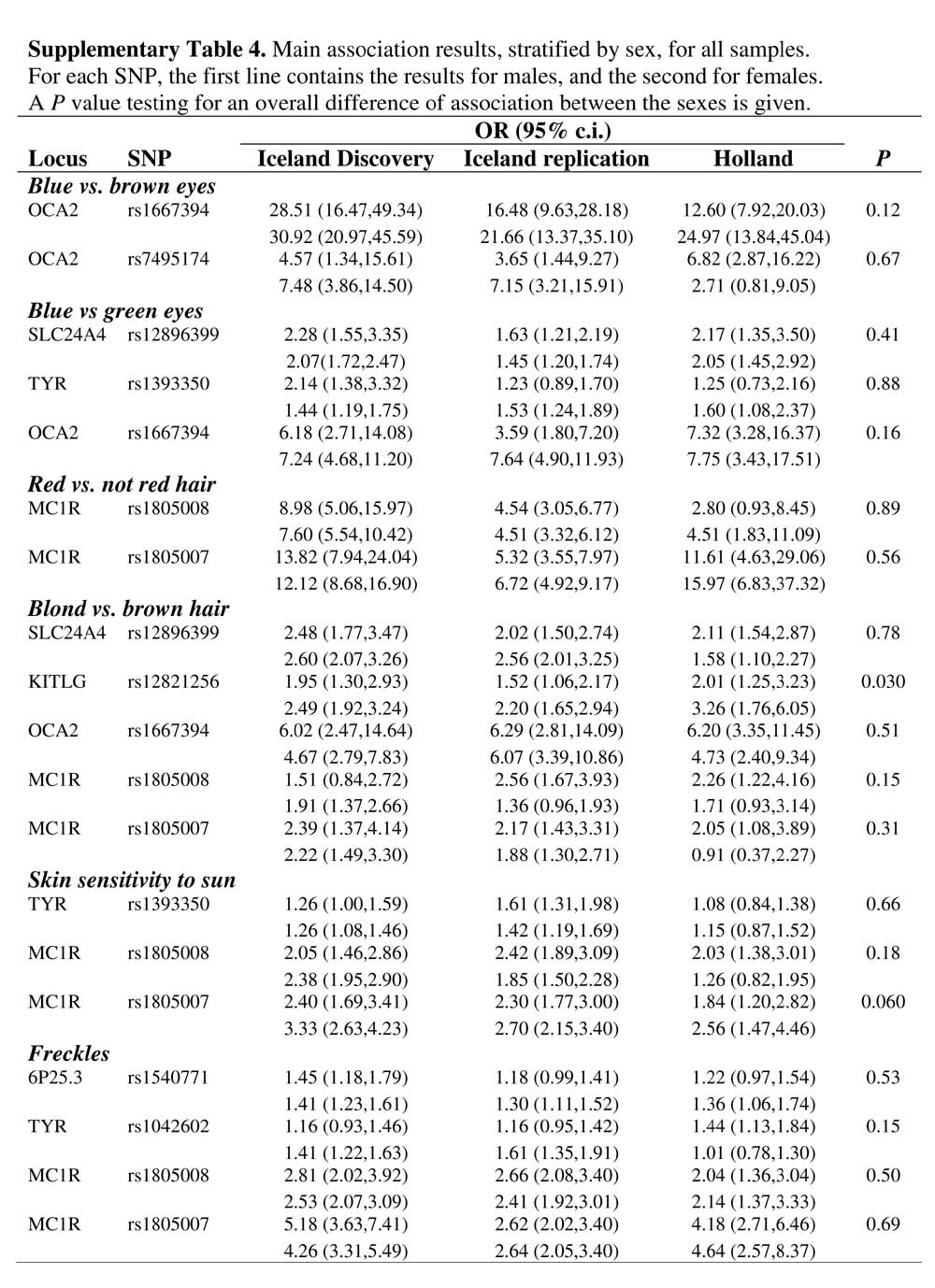 The authors don't want to make a judgment based on these data. But I'm not religious about 0.05 P values. And it looks like there's some action on KITLG anyhow. Labels: human biodiversity, Pigmentation
Monday, November 19, 2007
 An article in The New York Times, Are Scientists Playing God? It Depends on Your Religion, surveys attitudes toward cloning and biological engineering in general. Roughly the thesis being reported is that there is a trichotomy between post-Christian societies, traditional Christian societies and those where Eastern religions predominate. Generally I'm skeptical of these grand cultural typologies, but in this case I think there is an underlying component that explains a large part of the trend: the Roman Catholic Church has long opposed many forms of biological intervention and will no doubt oppose many forms of biological engineering which it deems unethical. Though I do not doubt the sincerity of the believers of the Roman Catholic religion in their adherence to their Church's position here, I think this is a case where the elite formulation of the clergy and intellectuals has really made a significant impact on public policy. Reading about the anti-abortion movement in the United States during early days after Roe vs. Wade it is clear that the Roman Catholics were at the forefront, and fundamentalist Protestants joined the fray quite a bit later. Similarly, when it came to eugenics laws they were quite widespread in Protestant countries, but the Catholic Church threw up a concerted and consistent resistance to them in nations where it was an institution which could affect public policy significantly. An article in The New York Times, Are Scientists Playing God? It Depends on Your Religion, surveys attitudes toward cloning and biological engineering in general. Roughly the thesis being reported is that there is a trichotomy between post-Christian societies, traditional Christian societies and those where Eastern religions predominate. Generally I'm skeptical of these grand cultural typologies, but in this case I think there is an underlying component that explains a large part of the trend: the Roman Catholic Church has long opposed many forms of biological intervention and will no doubt oppose many forms of biological engineering which it deems unethical. Though I do not doubt the sincerity of the believers of the Roman Catholic religion in their adherence to their Church's position here, I think this is a case where the elite formulation of the clergy and intellectuals has really made a significant impact on public policy. Reading about the anti-abortion movement in the United States during early days after Roe vs. Wade it is clear that the Roman Catholics were at the forefront, and fundamentalist Protestants joined the fray quite a bit later. Similarly, when it came to eugenics laws they were quite widespread in Protestant countries, but the Catholic Church threw up a concerted and consistent resistance to them in nations where it was an institution which could affect public policy significantly.There are also specific and general problems with the typology. Consider the specific: Asia offers researchers new labs, fewer restrictions and a different view of divinity and the afterlife. In South Korea, when Hwang Woo Suk reported creating human embryonic stem cells through cloning, he did not apologize for offending religious taboos. He justified cloning by citing his Buddhist belief in recycling life through reincarnation. Hwang Woo Suk is a convert from Christianity to Buddhism. South Korea is a nation that is about 1/2 non-affiliated, 1/4 Buddhist and 1/4 Christian. Its ethical culture has been traditionally dominated by Confucianism, and there is a powerful substratum of indigenous shamanistic religion which suffuses the practices and outlooks of Christians & Buddhists alike. Christianity is gaining ground among the youth and in the educated segment of the population, and is the dominant religion in Seoul. The last two presidents of South Korea have been Roman Catholic, and that denomination is generally considered the most well educated, affluent and liberal of the religious pillars in South Korean society. South Korea also sends out the most Christian missionaries to the rest of the world aside from the United States. Christian fundamentalists in South Korea have even engaged in iconoclastic violence against Buddhist religious art and statuary. And yet South Koreans were also rather proud of their "cloning research." Then there is the biggest general issue with the typology: By contrast, in the Judeo-Christian tradition, God is the master creator who gives out new souls to each individual human being and gives humans "dominion over soul-less plants and animals. To traditional Christians who consider an embryo to be a human being with a soul, it is wrong for scientists to use cloning to create human embryos or to destroy embryos in the course of research. I think the term Judeo-Christian is stupid. In any case, not only are there very few Jews in the world, their attitude toward biological engineering tends to be pragmatic and consequentialist from what I can tell. There is one religious group which is left out the typology: Islam. About 15-20% of the world's population this seems like a large oversight. There don't seem to be many laws about cloning in the Muslim world, but take a look at abortion laws. Their objection to interventions might be less coherent or precise than those of Roman Catholics, but they seem to mirror them pretty well. The New York Times piece also points out that in the post-Christian world, such as Sweden, there is a fear of some sorts of biological changes due to a resurgence in a form of natural religion or spirituality. This shouldn't surprise; the decline of institutional Christianity in northern and eastern Europe has been met with both a rise in a scientific materialist outlook, but even more significantly an unspecified monistic theism reminiscent of pre-Christian traditions. The Left-Right convergences alluded too suggest to me that the typology is too coarse and inchoate. There is a universal "Yuck" within our species, probably rooted in our cognitive hardware. Channeling the impulses culturally can be a tricky thing. For instance, the Japanese and Israelis are far less advanced than Americans in their acceptance or practice of organ donation, generally due to religious rationales. Obviously the Japanese and Israelis don't share a common spiritual root or background. Note: I place an emphasis on the Catholic Church as an institution affecting public policy because, for example, abortion rates of Catholics in the United States are at the national average. Moral suasion can only go so far, especially when individuals are making personal utility calculations. Labels: Bioethics
PLOS early release, Discerning the ancestry of European Americans in genetic association studies:
We have analyzed four different genome-wide data sets involving European American samples, and demonstrated that the same two major axes of variation are consistently present in each data set. The first major axis roughly corresponds to a geographic axis of northwest-southeast European ancestry, with Ashkenazi Jewish samples tending to cluster with southeastern European ancestry; the second major axis largely distinguishes Ashkenazi Jewish ancestry from southeastern European ancestry. The whole thing is free. Nothing too surprising, just pushing the decimal places further to the right, which is always a good thing when considering something which has medical applications. Labels: Genetics
Part 1 of these notes discussed the general meaning and use of the concepts of correlation and regression. The notes are intended to provide background for other posts I am planning, but if they are of any use as a general introduction to the subject, so much the better.
Part 2 discusses some problems of application and interpretation, such as circumstances that may increase or reduce correlation coefficients. I emphasise that these notes are not aimed at expert statisticians, but at the (possibly mythical) 'intelligent general reader'. I hope however that even statisticians may find a few points of interest to comment on, for example on the subjects of linearity, and the relative usefulness of correlation and regression techniques. Please politely point out any errors. Apart from questions of interpretation, this Part contains proofs of some of the key theorems of the subject, such as the fact that a correlation coefficient cannot be greater than 1 or less than -1. There is nothing new in these proofs, but I did promise to give them, and personally I find it frustrating when an author just says 'it can be proved that...' without giving a clue how it can be proved. Readers who already know proofs of the main theorems, or are prepared to take them on trust, may prefer to go straight to the section headed 'Changes of Scale'. Like Part 1, this Part does not deal with questions of sampling error. Except for a few passing comments, this Part deals only with bivariate correlation and regression. I am aware that some issues, such as linearity, arise equally (if not more seriously) in the multivariate case. Part 3, if and when I get round to it, will deal with the basics of multivariate correlation and regression. Notation These notes avoid using special mathematical symbols, because Greek letters, subscripts, etc, may not be readable in some browsers, or even if they are readable may not be printable. The notation used will be the same as in Part 1, with the following modifications. In Part 1, the correlation between x and y was denoted by r_xy, the covariance between x and y by cov_xy, the regression coefficient of x on y by b_xy, and the regression coefficient of y on x by b_yx. Since this Part deals only with the correlation of two variables, there will be no ambiguity if the correlation between x and y is denoted simply by r, and their covariance simply by cov. It is necessary to distinguish between the regression of x on y and the regression of y on x, and the coefficients will be denoted by bxy and byx respectively, without the subscript dashes used in Part 1 . These expressions could admittedly be confused with 'b times x times y', but I will avoid using the sequences bxy or byx in this sense. As pointed out in Part 1, for theoretical purposes it is often convenient to assume that variables are expressed as deviations from the mean of the raw values. In this Part the variables x and y will stand for deviation values unless otherwise stated. As previously, S stands for 'sum of', s stands for 'standard deviation of', ^2 stands for 'squared', and # stands for 'square root of'. The derivation of the coefficients As noted in Part 1, the Pearson regression of x on y is given by the coefficient Sxy/Sy^2, where x and y are deviation values. This is the formula which minimises the sum of the squares of the 'errors of estimate', in accordance with the Method of Least Squares. As it is the most fundamental theorem of the subject, it is worth giving a proof, using elementary calculus. (The result can be obtained without explicitly using calculus, but the explanation is then rather longer.) We want to find a linear equation, of the form x = a + by, such that the sum of the squares of the errors of estimate, S(x - a - by)^2, is minimised. Provided the x and y values are expressed as deviations from their means, the constant a must be zero. (If we use raw values instead of deviation values, a non-zero constant will usually be required.) The sum of squares S(x - a - by)^2 can be expanded as Sx^2 + Na^2 + b^2(Sy^2) - 2bSxy - 2aSx + 2abSy. But the last two terms vanish, as with deviation values Sx and Sy are both zero. This leaves Na^2 as the only term involving a, and Na^2 has its lowest value (for real values of a) when a = 0. At its minimum value the expression S(x - a - by)^2 therefore reduces to S(x - by)^2. It remains to find the value of the coefficient b for which S(x - by)^2 is minimised. This expression may be regarded as a function of b, which may be expanded as: f(b) = Sx^2 + b^2(Sy^2) - 2bSxy where Sx^2, Sy^2, and Sxy are quantities determined by the data. Applying the standard techniques of differentiation, the first derivative of f(b), differentiated with respect to b, is 2bSy^2 - 2Sxy. According to the principles of elementary calculus, if the function has a minimum value, its rate of change (first derivative) at that value will be zero, so to find the minimum (if there is one) we can set the condition 2bSy^2 - 2Sxy = 0. Solving this equation for b, we get b = Sxy/Sy^2 as a unique solution. In principle, this could be a maximum or a stationary point rather than a minimum, but it can be confirmed that for values of b either higher or lower than Sxy/Sy^2 the function f(b) has a higher value. Therefore b = Sxy/Sy^2 gives a unique minimum value for the sum of squares, and may be designated as bxy, the required coefficient of the regression of x on y. The best estimate of x, for a given value of y, is x = (bxy)y. By similar reasoning we can derive Sxy/Sx^2 as the coefficient of the regression of y on x. The correlation coefficient r can then be derived as the mean proportional between the two regression coefficients, or in the Galtonian manner by 'rescaling' the x and y values by dividing them by sx and sy respectively, giving r = Sxy/Nsx.sy. These formulae use deviation values of x and y. If we prefer to use raw values, the appropriate formulae can be obtained by substitution. Using x and y now to designate raw values, the deviation value of x equals x - M_x, where M_x is the mean of the raw values. Similarly the deviation value of y equals y - M_y. Substituting these expressions for the deviation values of x and y in the above equation x = (bxy)y, we get the formula for raw values x = (bxy)y + M_x - (bxy)M_y. By the same methods we get y = (byx)x + M_y - (byx)M_x. These equations can be represented graphically by straight lines intercepting the axes at points determined by the constants [M_x - (bxy)M_y] and [M_y - (byx)M_x], and with slopes determined by the coefficients bxy and byx. The range of coefficients For any positive value of r, expressed in the form Sxy/Nsx.sy, the regression coefficients could range from 0 to infinity, since there is no upper or lower limit on the ratios sx/sy and sy/sx. Similarly, for any negative value of r, the regression coefficients could range from 0 to minus infinity. Unless sx and sy are equal (in which case regression and correlation coincide), one regression coefficient must always be greater and the other less than r. If the regression coefficients are reciprocal to each other (e.g. 2/3 and 3/2), the correlation will be perfect (1 or -1) and there will be a single regression line. Unlike the regression coefficients, the correlation coefficient r can only range from 1 to - 1. Introductory textbooks often state this without proof, but it is a simple corollary of another fundamental theorem on correlation. Unless the correlation is perfect (1 or -1), there will be a certain scatter of the observed values of x around the value estimated by the regression of x on y. The coefficient of regression of x on y is Sxy/Sy^2 or r(sx/sy). The estimated values of x for the corresponding values of y are therefore r(sx/sy)y, and the errors of estimate (i.e. the differences between the actual values and the estimated values) will have the form [x - r(sx/sy)y]. But these errors will themselves have a variance, which we may call Ve = [S[x - r(sx/sy)y]^2]/N. [Added: This assumes that the mean value of the errors is zero. Using deviation values of x and y this quite easy to prove, as the mean of the errors is S[x - r(sx/sy)y]/N = (Sx - r(sx/sy)Sy)/N = (0 - 0)/N.] With a little manipulation it can be shown that [S[x - r(sx/sy)y]^2]/N equals (1 - r^2)Vx. [See Note 1.] So we reach the important result that the variance of the errors of estimate of x, as estimated from the regression of x on y, is (1- r^2) times the full variance of x. In other words, the variance of the observed x values around the estimated values is reduced by the proportion r^2 (the square of the correlation coefficient) as compared with the full variance of the x values. It is therefore often said that the correlation of x with y explains or accounts for r^2 of the variance of x. Similarly, it accounts for r^2 of the variance of y. To mark the importance of r^2 it is often known as the coefficient of determination. Since r is a fraction (unless it is 1 or -1), r^2 is smaller than r. The amount of variance explained by r declines more and more rapidly as r itself declines, and a correlation of less than (say) .3 explains very little of the variance. The term 'explained' is to be understood purely in the sense just described, and does not necessarily imply a causal explanation. The estimated values of x themselves have a variance equal to [S[(bxy)y]^2]/N = [S[r(sx/sy)y]^2]/N = [(Sy^2.r^2)Vx/Vy]/N, which can be simplified to (r^2)Vx. Therefore Vx, the total observed variance of x, can be broken down into two additive components, (r^2)Vx + (1 - r^2)Vx, representing the variance of the estimates themselves and the residual variance not accounted for by the correlation. The closer the correlation (positive or negative), the more of the variance is 'explained'. If the correlation is perfect (1 or -1) then r^2 = 1 and it 'explains' all the variance of x, since there are no errors of estimation at all. If a correlation could be greater than 1 or less than -1, then the variance of the errors, (1- r^2)Vx, would be negative. But a variance cannot be negative, so the correlation coefficient r cannot be greater than 1 or less than -1. Changes of Scale The value of the correlation coefficient is unchanged (except sometimes for a reversal of sign) if all the x values, or all the y values, or both, are added to or multiplied by the same constant. For example, if we add a constant k to all the raw x values, then the mean is also increased by k, so the deviation values, the covariance, and the standard deviation, are all unchanged, and therefore the correlation coefficient r = cov/sx.sy itself is unchanged. If instead of adding k we multiply all the raw x values by k, where k is positive, then the mean, the deviation values, and the covariance are also multiplied by k. But so is the standard deviation, so the factor k cancels out of k.cov/k.sx.sy = r, leaving the correlation coefficient itself unaffected. (If k is negative, the sign of r is reversed, since the covariance changes its sign but the standard deviation does not.) Since each such operation of adding and multiplying (in the manner described) leaves r unchanged, they can be repeated any number of times, and in any order, and still leave r unchanged. This can be useful for practical purposes, because it means that if a correlation coefficient is calculated for any convenient set of x and y values, it will still be valid if we add or multiply by k in the way described. Or we might at first be faced with an inconvenient set of values and then convert them to a more manageable set. It also means that the value of the correlation coefficient is unaffected by a change of scale in one or both variables, for example by measuring in inches instead of centimetres. A further practical implication is that correlation coefficients may be unaffected, or only slightly affected, even by major changes in the population, provided these affect all members of the population in a similar way. For example, the correlation between the heights of fathers and sons may be unchanged even if the sons grow much taller than the fathers, provided the growth is uniform in absolute or proportionate amount. Another possible example is bias in mental tests. It is sometimes supposed that if test results show the same correlation with some external criterion in two different populations, then the test must be 'unbiased' with respect to those populations. As it stands, this inference is unjustified, because the correlations would be unchanged if all the test scores in one population were arbitrarily raised (or lowered) by the same amount, which would surely be a form of bias. The effect of changes of scale on regression is somewhat more complicated. If we always measure the variables in deviation units, relative to their current means, then the regression coefficients will not be affected by adding constants to one or both raw variables, since the deviation values, the covariance, and the standard deviations, are all unchanged, as in the case of correlation. This is not in general true if one or both of the variables are multiplied by constants. For example, if we multiply all of the y values by k, then Sxy, which is the numerator in the Pearson regression formula for bxy, will be multiplied by k, but the denominator, Vy, will be multiplied by k^2, so the regression coefficient as a whole will be divided by k. However, the value of the product (bxy)y will be unchanged, since one factor in the product is multiplied and the other divided by k. With deviation values the predicted value of the dependent variable is therefore not affected by a change of scale in the independent variable alone. If we use the regression formula for raw values, the matter is further complicated. Adding constants to one or both variables will usually affect the 'intercept' of the regression lines with the axes, but not the 'slope', whereas multiplying by a constant is likely to affect both slope and intercept. Linearity The above derivation of the regression and correlation coefficients assumes that the 'best estimates' of x given y, and y given x, can be expressed by equations of the form x = a + by and y = a + bx, which may be graphically represented as straight lines. For this reason they are usually known as coefficients of linear regression and correlation. [See Note 2 for this terminology.] The question may be asked whether the assumption of linearity is justified, either in general or in any particular case. If the correlation between the variables is perfect (1 or -1), the regressions will predict the value of the variables without error, and in a graphical representation the points representing the pairs of associated values will all fall exactly on the regression line (which in this case is the same for both variables). Here the description 'linear regression' is obviously justified. But perfect correlation is unusual, and more generally there will be some scatter of values around the regression lines. The usual criterion of linearity, adopted from Karl Pearson onwards, is that for each value (or a narrow range of values) of the independent variable, the mean of the associated values of the dependent variable (the associated 'array' of values) should fall on the regression line. By this criterion, if the mean values of all arrays fall exactly on the regression line, the regression is perfectly linear. Linear or approximately linear regression, in this sense, is quite common. Notably, it occurs when the distribution of both variables is normal or approximately normal. (Strictly, when the bivariate distribution is normal. The distinction would take too long to explain here.) Francis Galton and Karl Pearson confined their original investigations to this case. Udny Yule extended the treatment of correlation and regression beyond this 'bivariate normal' case, but he considered that linear regression 'is more frequent than might be supposed, and in other cases the means of arrays lie so irregularly, owing to the paucity of the observations, that the real nature of the regression curve is not indicated and a straight line will give as good an approximation as a more elaborate curve'. Statisticians differ in the importance they attach to linearity. Some say that if there is any significant departure from linearity, then the Pearson regression and correlation formulae are invalid and should not be used. They will give an inefficient estimate which leaves larger 'errors' than would be possible with a more sophisticated approach. Others take a more relaxed view, saying that if the non-linearity is not extreme, a linear regression is a useful approximation. Any non-zero Pearson regression will 'explain' some of the variance in the data, and give a better estimate (on average) than simply taking the mean of the dependent variable. Whether the increase in the 'errors' is a serious problem will depend in part on the purposes of the investigation. If the consequence of error in estimation is a large financial cost, or an injustice to individuals, then it is desirable to seek a more accurate formula. If the departures from linearity are considered too large, alternatives to simple linear regression may be tried. For example a linear regression may still be obtained if we substitute a suitable function of one or both variables in place of the original values. The best known case (and perhaps the only one commonly arising in practice) is where the logarithms of the original values show a linear regression. This can arise if one of the variables grows or declines at a steady rate of 'compound interest' in relation to the other. Alternatively, the researcher may try fitting a curve (such as a polynomial curve of the form x = ay + by^2 + cy^3....) to the data instead of a straight line, the aim being to pass the curve through the means of 'arrays' of the dependent variable. But there is no guarantee that any simple curve will give a good fit to the data, or that it will be any more revealing about the underlying relationships of the variables than a straight line. It should also be emphasised that, unlike with linear regression, there will not necessarily be any simple relationship between the regression of x on y and that of y on x. Each non-linear regression curve has to be separately fitted to the data. The regressions of x on y and y on x may be quite different in form. Having fitted a curve to the data, as a non-linear regression of x on y or y on x, one may calculate how much of the variance in the dependent variable is 'explained' by the regression. But in the non-linear case there is no simple formula for this, and it will not in general be the same for both regressions. Although the term 'non-linear correlation' is sometimes used, one cannot properly speak of the correlation between two variables in the non-linear case. In some cases a non-linear regression formula may give a good fit to the data but still be of doubtful value. Especially in the social sciences, departures from linearity may be due to lack of homogeneity in the population, for example differences of age, sex, race, class, etc. The relationship between two variables (e.g. educational achievement and IQ) might be linear within each subgroup, but quantitatively different in each such group. The 'best fit' regression line for the whole population would then probably be non-linear, but would depend on the composition of this particular population and have no wider application. Where a population is known to be heterogeneous with respect to the variables of interest, it would be better to disaggregate the data and treat each group separately. Failing that, a straight line regression, which averages out the characteristics of the different groups, may be the most useful single indicator. It is my impression that non-linear regression and correlation are not used much in practice outside the physical sciences, where it is reasonable to expect very precise relationships between variables. Regression versus correlation? Regression and correlation are closely related, both mathematically and historically. Some statisticians have however contrasted the roles of regression and correlation, and see one as more useful than the other, or as having different fields of application. In the time of Karl Pearson and his students the main emphasis was put on the correlation coefficient, which is independent of scale and gives a measure of the extent to which one variable is 'explained' by another. A reaction against this emphasis on the correlation coefficient was led by R. A. Fisher, who said: 'The idea of regression used usually to be introduced in connexion with the theory of correlation, but it is in reality a more general, and a simpler idea; moreover, the regression coefficients are of interest and scientific importance in many classes of data where the correlation coefficient, if used at all, is an artificial concept of no real utility.' (R. A. Fisher, Statistical Methods for Research Workers, 14th edition, 1970, p.129. The quoted passage goes back to the 1920s.) Cyril Burt remarked that 'A correlation coefficient is descriptive solely of the set of figures on which it is based: it cannot profess to measure a physical or objective phenomenon, as a regression coefficient or a covariance may under certain conditions claim to do' (The Factors of the Mind, 1940, p.41). The American statistician John Tukey once joked that he was a member of a 'society for the suppression of correlation coefficients - whose guiding principle is that most correlation coefficients should never be calculated'. More recently, M. G. Bulmer has said: 'It is now recognised that regression techniques are more flexible and can answer a wider range of questions than correlation techniques, which are used less frequently than they once were' (Principles of Statistics, Dover edn., p.209). This contrast between regression and correlation may seem surprising, as the Pearson coefficients of correlation and regression differ only by a factor of scale, and can be regarded as standardised and unstandardised variants of the same statistic. If we have the information necessary to calculate one of them, we can also calculate the others, since they all involve the covariance of x and y, and the data required for calculating the covariance is sufficient also to determine the coefficients of correlation and regression. But this overlooks the fact that regression coefficients can be estimated from more limited data, without knowing the covariance in the population as a whole. As Fisher pointed out, if we want to know the expected value of x for a given value of y, it is possible to estimate the regression function (whether linear or not) by taking samples of data from a few selected parts of the range of y. Unlike the correlation coefficient, the regression estimate is unaffected by errors in the measurement of x (the dependent variable), provided these go equally in either direction. The correlation coefficient may also vary according to the nature of the sample (such as restriction of range), in ways that do not affect the regression coefficients so strongly. A correlation coefficient cannot be considered 'objective' unless it is based on a random or representative sample of the relevant population. However, provided this condition is met, the correlation seems to be just as much an objective characteristic of the population as the regressions. It may be argued that the regression coefficients are less likely to vary dramatically in moving from one population to another, but one would wish to see empirical evidence for this in any particular field. The use made of correlation and regression in practice depends on the field of study. Correlation coefficients are still very widely used in psychometrics, where the scale of measurement is often arbitrary and regression coefficients would vary with the choice of scale. In the social sciences, correlation is probably less widely used, whereas regression analysis (usually multivariate regression) is one of the main instruments of research. Problems of interpretation Correlation and regression raise various problems of interpretation, some of which are well known, others less so. To list some of the more important ones: a) Restriction of range If the x variable, or the y variable, or both, cover only a limited part of the whole population, the correlation will usually be weakened. b) Aggregation of data If a correlation is calculated between data that have been aggregated or averaged in some way, e.g. geographically, the correlations will often be higher - sometimes much higher - than if they were calculated at a less aggregated level. Points (a) and (b) are both discussed in an earlier post here. c) Correlation due to pooling of heterogeneous groups If we have two population groups, which have different means for the x and y variables, then if the data from the two groups are combined there will be a correlation between x and y even if there is no correlation within each population group. d) Correlation due to mathematical relationships If one of the variables is actually a part of the other (e.g. length of leg as a part of total height), we will naturally expect there to be a correlation between them. Other mathematical relationships between the variables may also give rise to correlations. For example, if the corresponding x and y values are each arrived at by dividing some data by a third variable, which has the same value for the x and y items in each pair but different values for different pairs, then a correlation will arise (sometimes known as 'index correlation') even if the initial data are uncorrelated. Karl Pearson described these as 'spurious correlations', but whether they are really to be regarded as spurious depends on the circumstances. e) Correlation between trends If the x and y data represent quantities which vary over time, they will often show some long term trend: a tendency (on the whole) either to increase or decrease. If any two such data sets are paired, with the corresponding x and y items in the same chronological order, they will show a correlation: positive if the two trends are in the same direction, negative if they are in opposite directions. Such correlations can be very high. I once constructed two artificial data series, with 20 items of increasing size in each, and deliberately tried not to make the increases too regular, but still found a correlation between the two series of .99! Such correlations can arise regardless of the nature of the data. For example, there would doubtless be a positive correlation between prices in England from 1550 to 1600 and real incomes in Japan from 1950 to 2000 (paired with each other year by year), because there was a rising trend in both. In this case no-one is likely to suppose that there was a causal connection between the two trends, but in other cases there is a real danger. If the two variables are of such a kind that there plausibly may be a causal connection, and they are observed over the same period in the same place, there is a risk that any correlation will be taken more seriously than it should be. For example, if we measure the consumption of pornography and the incidence of rape in the same decade in the same country, there is likely to be some correlation between them. If it is positive, the puritan will say: 'Aha, pornography causes rape!'. If it is negative, the libertarian will say: 'Aha, pornography provides a safe outlet for sexual urges!' Both conclusions are unjustified, because the mere existence of a correlation between two trends, no matter how strong, is almost worthless as evidence of anything. Yule called these 'nonsense correlations'. He pointed out that in principle a similar problem could arise with geographical trends, such as a north-south gradient, though it was more difficult to find plausible examples. A slightly different case is correlation with wealth or income. Very many traits are correlated with economic prosperity (individual or national), so they are also likely to be correlated with each other. In this case a correlation, even a strong one, between traits is not good evidence of any direct causal connection between them. I would suggest that in the human sciences (psychology, sociology, etc) any very strong correlation (higher than, say, .9) should be viewed with suspicion, and we should examine whether some statistical technicality (such as a grouping effect) is behind it. f) Correlation and causation In every textbook the warning is given that 'correlation does not imply causation'. Up to a point this is correct: the examples of index correlations, and of correlations between trends, show that there may be correlations even when there is nothing that we would properly describe as a causal relationship. Unfortunately the textbooks seldom go on to say that correlation usually does imply a causal connection of some kind, even if it is obscure and indirect. The business of the investigator is then to formulate hypotheses to explain the connection, and to find ways of testing them. Sewall Wright's path analysis was designed for this purpose. The main problem arising is how to interpret the relations between more than two variables. g) Regression towards the mean The concept of regression also involves a danger of fallacies or paradoxes, which I discussed here. Note 1: We start with the equation (1) Ve = [S(x - r.y.sx/sy)^2]/N. Expanding the expression in square brackets we get: (2) Ve = (Sx^2 - 2Sxy.r.sx/sy + Sy^2.r^2.Vx/Vy)/N. But Sx^2 = NVx, also Sxy = Nr.sx.sy, and Sy^2 = NVy, so substituting these expressions where appropriate in equation (2) we get: Ve = (NVx - 2Nr.sx.sy.r.sx/sy + r^2.NVy.Vx/Vy)/N = (NVx - 2r^2.NVx + r^2.NVx)/N = (1 - r^2)Vx. Note 2: Some confusion has arisen about the meaning of the terms 'linear' and 'non-linear' regression. Traditionally, at least until the 1970s, the term 'linear regression' was confined to cases where the regression equation can be represented graphically by a straight line (or by a plane or hyperplane in the multivariate case). For example: 'If the lines of regression are straight, the regression is said to be linear' (G. Udny Yule and M. Kendall, Introduction to the Theory of Statistics, 14th edition, 1950, p213), and 'When the regression line with which we are concerned is straight, or, in other words, when the regression function is linear.... ' (R. A. Fisher, Statistical Methods for Research Workers, 14th edition, 1970, p131). Many other examples could be cited. Regression that is not linear in this sense was described as 'curvilinear' (Yule, p.213) or 'non-linear' (Yule, p.255). More recently some authors have extended the term 'linear regression' to a wider class of functions, including those previously described as 'curvilinear'. Those who adopt this new usage may even accuse those (probably still the majority) who follow the traditional usage of being in error. One wonders what Fisher would have said. Labels: Burbridge  I'm interested in blue eyes. Specifically, I wonder why they're around at all. Unlike blonde hair, there's only one region of the world where blue eyes are extant at high frequencies, and there is a pretty regular drop off as a function of distance. It seems that variants of OCA2 are associated with blue eyes in Europeans. If you check Haplotter it looks like the region around this gene has been subject to a powerful bout of recent selection (i.e., within the last 10,000 years). Why this selection? Well, there's no definitive explanation yet. But I don't want to focus on hypotheses for why OCA2 has been subject to selection as much as what correlates there seem to be with the phenotype of blue eyes. Specifically, behavioral correlates. I'm interested in blue eyes. Specifically, I wonder why they're around at all. Unlike blonde hair, there's only one region of the world where blue eyes are extant at high frequencies, and there is a pretty regular drop off as a function of distance. It seems that variants of OCA2 are associated with blue eyes in Europeans. If you check Haplotter it looks like the region around this gene has been subject to a powerful bout of recent selection (i.e., within the last 10,000 years). Why this selection? Well, there's no definitive explanation yet. But I don't want to focus on hypotheses for why OCA2 has been subject to selection as much as what correlates there seem to be with the phenotype of blue eyes. Specifically, behavioral correlates.There's a fair amount of recent work in this area, but reading Racial Adaptations I stumbled upon some older studies, and, a model to explain the outcomes which I'm not really qualified to judge. So I'm going to report and let you decide, and hopefully, inform (especially those of you with cognitive neuroscience backgrounds). So here I go. From page 66: ...eyes of different colors are related to differents in perception and innate behavior, as psychologists have discovered.23 Some of their tests have shown that dark-eyed persons are more aware of color and lighter-eyed ones of form; the former prefer bright hues and the latter lighter ones. Light eyes tend to envision panoramas, dark ones to concentrate on details I don't know anything about fashion or design, but I wonder if those of you who know this area (assman?) might be able to map some macrosocial trends back to these individual differences? After all, the vast majority of Scandinavians are blue eyed, and they've produced a fair amount of modern design. While Italians are well represented in the world of fashion and the arts. And the frequencies of eye colors are probably inverted in these two populations. In any case, moving on, later on the page: Behavioral variations are focused on the differences between "self-paced" and "reactive" responses to sudden stimuli. In the first subjects follow a well-known plan of animal behavior of pausing and deliberating before decision. In the second the subject flies into instant action (in animals), to attack or to flee. Of course, these behaviors are elaborated in man to govern many more-complex and subtler actions in speech and deed. That's a lot to throw at you, but pretty much line with more recent work. The author does note that these studies were performed upon subjects of European ancestry. Whatever differences one can see between groups of blue and brown eyed Europeans, obviously it wouldn't predict to other genetic backgrounds. East Asians tend to exhibit some of the same behavioral tendencies vis-a-vis Europeans that blue eyed Europeans exhibit vis-a-vis brown eyed ones. Obviously brown eyes can't explain this since East Asians have brown eyes. This isn't that strange, lots of the recent research in regards to human evolution suggests that East Asians and Europeans can converge upon the same phenotype via alternative genetic pathways. Blue eyes may simply be a byproduct of selection for another phenotype. But on to the author's model, which requires some knowledge of cognitive neuroscience and brain chemistry to evaluate. From page 74: Few people other than ophthalmologists seem to have looked at retinas, nor to have considered it remarkable that the fundus is of virtually the same color as the person's skin and for obvious reason that the underside of the retina is epidermis At this point the author draws upon some photographs of the retinas of various racial groups, and observes the variation in color. He takes lithographs of these photos and basically measures the amount of light which can penetrate them. Here is the exposition that is relevant: The Negro and the mulatto get 1.75 fcp; the Hindu and the American Indian 1.16 fcp; the brunet European 0.66 fcp; and the Chinese, the blond and the albino get 0.22 fcp. The Negro's and the mulatto's retinas let through eight times as much light as did those of the Chinese, the blond, and the albino. OK, here's the part where he lays out his argument for color and behavior: Once inside the cranial cavity, neural impulses produced by the visible light that has passed through the retinal screen follow one of two paths. One lot goes to the hypothalamus...This part of the brain is the primary control tower of the central nervous system for almost all of the self-starting and self-regulating activity of the body-the sleep cycle, body temperature, the digestive process, fighting and loving. That was a lot to throw out there, but the main reason I'm posting this is so that cognitive neuroscience people can throw cold water on this model or not. Obviously a lot has happened in neuroscience since the 1970s, when the author thought this idea up. Myself, I tend to get confused on the various biochemicals which modulate brain chemistry and all the different pathways and modulations, so clarification would be nice too. Two points I'd also like to point out. 1) the Chinese clustered with the blond European in terms of the retina light values. 2) If the amount of light which manages to get through the retina is a major issue, that can explain variation by latitude and climate in terms of temper and personality, since obviously the amount of sunlight and radiation which reaches the surface varies a great deal. Labels: human biodiversity, Pigmentation
In the interests of putting informative physical anthropological data on the web, here is something I scanned out of Racial Adaptations. The map below the fold combines both hair & eye color data.
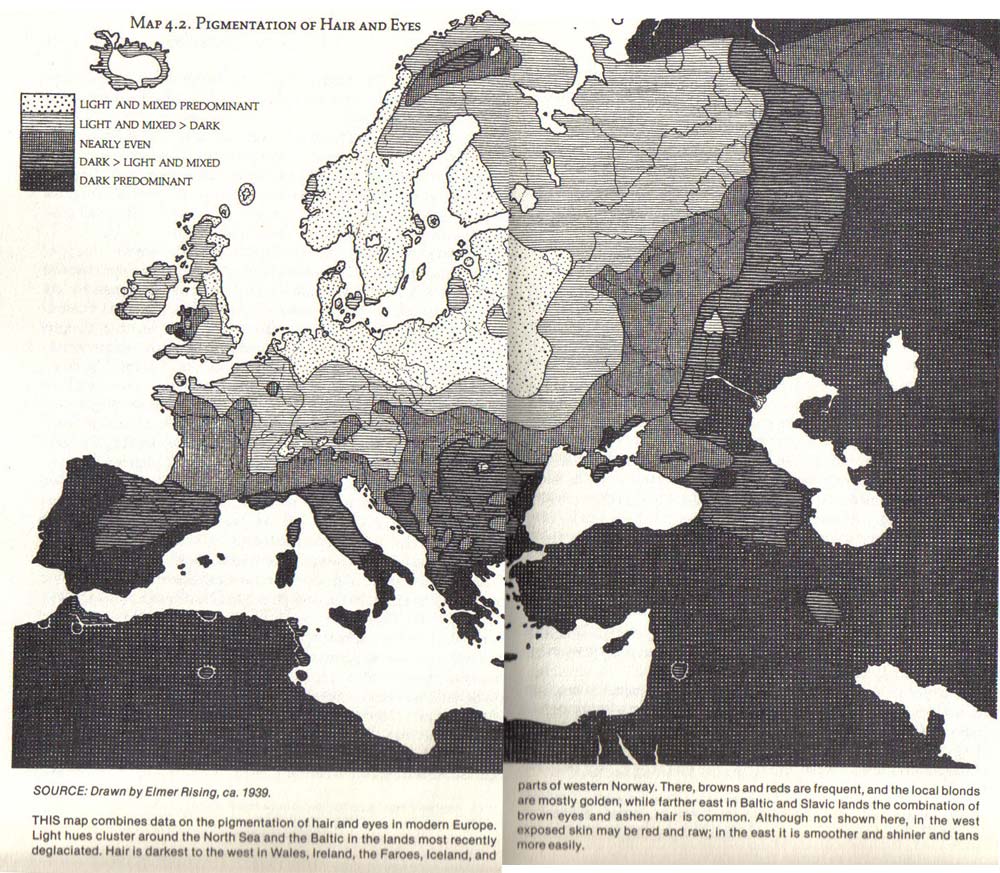 Labels: human biodiversity, Pigmentation
Sunday, November 18, 2007
Over at Edge Armand Leroi was interviewed about human genetics & variation. Most of the talking points are based on his book Mutants.
Labels: Genetics
Nothing too surprising in this story about attitudes toward alcohol in Europe. From Finland:
Since the government cut tax on alcohol by one third in March 2004, deaths and diseases from alcohol have all jumped by similar amounts in hard-drinking Finland. People respond to tax incentives! Labels: culture  In PLoS Genetics, there's a report on the identification of a locus that leads to white coat color in horses. This locus is KIT, a proto-oncogene (ie. certain mutations in this gene lead to increased cell growth and sometimes cancer) important for the survival of melanoblasts early in development. It's a nice story on its own, and the authors have an interesting historical genetics perspective: In PLoS Genetics, there's a report on the identification of a locus that leads to white coat color in horses. This locus is KIT, a proto-oncogene (ie. certain mutations in this gene lead to increased cell growth and sometimes cancer) important for the survival of melanoblasts early in development. It's a nice story on its own, and the authors have an interesting historical genetics perspective:Two thousand years ago, the Romans already knew of the phenotypic differences of depigmented horses, which they described as candidus (white) or glaucus (grey). The Roman historian Tacitus described the use of sacred white horses for auguries by German tribes. The so-called white horse of the Saxons is depicted on the flags of the German states of Lower Saxony and North Rhine-Westphalia. It is thus of considerable historic interest to trace the origins of white horses, particularly because the nature of their white color can have different causes, some of which are KIT mutations such as those described here. We do not know whether the Roman terms candidus and glaucus actually correspond to our modern coat color designations of white and grey. Archaeogenetics on historic DNA samples may help to identify the genetic constitution of these horses.But something about that gene name bothered me: where had I heard it before? Ah yes, there was a recent report of an association with variants near KITLG (KIT ligand; ie. a binding partner of KIT) and blonde hair in humans. The genetic architecture underlying pigmentation isn't all that different across mammals, of course, so this isn't surprising. But still, it's nice to see these connections-- sometimes, biology makes sense. Labels: Genetics, Pigmentation
Saturday, November 17, 2007
Over at Overcoming Bias Eliezer sings the praises of simple math. Steve was the first person to bring to my attention this phenomenon. For me, a little algebra, probability and statistics goes a long way in making one's thoughts more precise and rigorous (even one's own internal monologue). You can attempt this through pure verbal description, but unfortunately the precision may not be perceived the same from different vantage points. In other words, verbal arguments often tend to communicate different things to different people (or different things to the same person at different times) because of subtle and implicit semantic interpretations (the mental algebra obviously works out differently if the coefficients in front the variables vary from person to person). If you speak in cautious and specific philosophical language it may only clarify the misunderstandings further.* Another angle is that of simple data analysis. Half Sigma and Inductivist do this well. The data is out there, insight will come.
* This is confusing. Clarify misunderstandings? If two people are discussing a topic and their understanding of the terms is such that they have two different conceptions of what they are discussing, further specificity of the language won't necessarily bring them together, rather they simply clarify in their own minds their interpretation of the model. Labels: culture
Razib noted, in his post on the IQ-breastfeeding-FADS2 story, that it reminded him of research on MAOA. There's a reason: it's by the same group. In fact, the IQ study is the third in a "trifecta" of gene-environment interactions postulated by Avshalom Caspi and colleagues. Curious about whether their statistical methods were similar in all these studies, I went back to them.
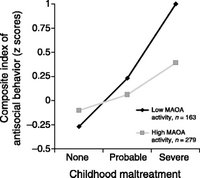 1. In 2002, the authors reported an interaction between variation in MAOA and childhood maltreatment on the probability of developing "antisocial problems". The relevant graph is on the right. It's important to keep in mind, from a statistical standpoint, what an interaction is: in a regression of variable Y on variable X, if the slope of the line significantly differs depending on another variable Z, one concludes for an interaction between Z and X. In this, the slopes do appear to be different, and the authors find this is indeed statistically supported. They don't include parental "antisocial behavior" as a covariate in their regression, either because they don't have that data or didn't think to include it. 1. In 2002, the authors reported an interaction between variation in MAOA and childhood maltreatment on the probability of developing "antisocial problems". The relevant graph is on the right. It's important to keep in mind, from a statistical standpoint, what an interaction is: in a regression of variable Y on variable X, if the slope of the line significantly differs depending on another variable Z, one concludes for an interaction between Z and X. In this, the slopes do appear to be different, and the authors find this is indeed statistically supported. They don't include parental "antisocial behavior" as a covariate in their regression, either because they don't have that data or didn't think to include it.  2. In 2003, the authors then genotyped another locus in the cohort studied above, this time the serotonin transporter. They reported a significant interaction between polymorphism in this gene and stressful life events on risk of depression. Again the relevant graphs are on the right. Across several measures of depression, there does appear to be an interaction. Again, no inclusion of parental phenotype in the regression. 2. In 2003, the authors then genotyped another locus in the cohort studied above, this time the serotonin transporter. They reported a significant interaction between polymorphism in this gene and stressful life events on risk of depression. Again the relevant graphs are on the right. Across several measures of depression, there does appear to be an interaction. Again, no inclusion of parental phenotype in the regression. 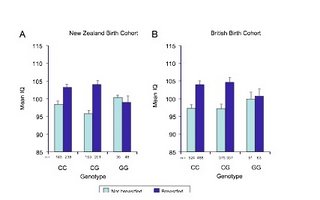 3. Now let's consider the IQ-FADS2 story. Again, they use the same cohort (as well as a replication cohort). This time, instead of genotyping known functional variants in a gene thought to be involved in the phenotype, they genotype a couple tagging SNPs in a gene picked through some spectacular logical leaps (1. there is a link between breastfeeding and IQ. 2. That link is modulted through fatty acid metabolism. 3. Of all the genes involved in fatty acid metabolism, the one of interest is FADS2). This has to change your priors on whether anything they find is real. Again, check the graph on the right: this time, they don't have the nice dose-response curve that they had in the others, so they go for a bar chart. And it does indeed look a little noiser. The replication, though, is something that wasn't present in the other studies. 3. Now let's consider the IQ-FADS2 story. Again, they use the same cohort (as well as a replication cohort). This time, instead of genotyping known functional variants in a gene thought to be involved in the phenotype, they genotype a couple tagging SNPs in a gene picked through some spectacular logical leaps (1. there is a link between breastfeeding and IQ. 2. That link is modulted through fatty acid metabolism. 3. Of all the genes involved in fatty acid metabolism, the one of interest is FADS2). This has to change your priors on whether anything they find is real. Again, check the graph on the right: this time, they don't have the nice dose-response curve that they had in the others, so they go for a bar chart. And it does indeed look a little noiser. The replication, though, is something that wasn't present in the other studies. The fact that they have a measure of maternal IQ but don't directly include it in the published multiple regression suggests that they tried it, but didn't like the results. They didn't include parental phenotype in any of their previous studies, but there, at least, there was some functional evidence linking the polymorphism and the phenotype. Here, there's nothing. Considering the fact mentioned in a previous post that other researchers find absolutely no evidence for link between IQ and breastfeeding (the entire basis for this study), this has to be classified as highly questionable. And regardless of the veracity of any gene-environment interactions here, the huge effects of breastfeeding on IQ shown by the authors are clearly artefacts of the heritability of IQ, and it's unfortunate that they are being propogated. Half Sigma is apoplectic about this; I'm not so much-- this is a case of researchers having a hammer (their cohort and a desire to find gene-environment interactions), and seeing every problem as a nail, not some ode to breast-feeding. Anyways, on a completely unrelated note, here's small nugget from their Supplementary Table 2, where they break down IQ by social class. I suppose I'd seen figures like this before (ie. in The Bell Curve), but it still gave me a start: Low class: 93.5 (11.6) Middle class: 100.5 (13.7) High class: 111.4 (12.8) In parentheses are standard deviations.
Friday, November 16, 2007
Socialism doesn't work people, haven't we learned that? Strike closes nearly 300 liquor stores in Finland.
Labels: Finn baiting  Bettany Hughes, our favorite pop classicist, is back with a new documentary, Athens: the dawn of democracy. It should be showing this Monday evening on your local PBS station if you live in the United States. I've recently expressed my skepticism at the democralatry which suffuses American discussion. Bettany Hughes, our favorite pop classicist, is back with a new documentary, Athens: the dawn of democracy. It should be showing this Monday evening on your local PBS station if you live in the United States. I've recently expressed my skepticism at the democralatry which suffuses American discussion.Labels: History
So picked up Michael Lynch's The Origins of Genome Architecture a bit worried, after all I don't have the marginal time to work through something like Genetics and Analysis of Quantitative Traits. Well, I didn't need to worry, I'm about half way through The Origins of Genome Architecture and it reads more like a manifesto than a text. Not that it isn't densely packed with references to the latest research (though I can see places where it is obvious it went to printing just a bit early), but the prose doesn't have the clunky flavor common to scientific textbooks coauthored by four or five different individuals. In other words, Lynch allows his voice to speak pretty clearly and unequivocally. Much of the material in The Origins of Genome Architecture is an amplification of previously published work (on some occasions he even simply interpolates prose you've seen in journal articles), which makes sense since Lynch notes that he's been working on this book for six years. Some of the articles he's published are obviously early leaks of ideas he formulated for book. In any case, I hope I won't ruin it for you when I tell you that Lynch makes the case that:
A subheading for The Origins of Genome Architecture could have been "Why R.A. Fisher was wrong." Lynch's case hinges quite a bit (so far) on genetic draft and how it relates to effective population size. The population genetics in this book is really low level, basically some algebraic manipulations which aren't difficult to follow if you simply read closely and think hard. He might refer to a diffusion equations, but Lynch won't derive it for you, you're presented with the neat formalism that pops out at the end of the process. Nevertheless, I do have to suggest that if you're someone without a biological education this book is going to be impenetrable. The population genetic math isn't very hairy, you can grasp the basic logic of the argument from the spare formalisms without the underlying nuts and bolts which connect the formulas, but the molecular genetic jargon will probably be too much for the typical uninitiated lay person. If your main exposure to biology is this weblog, then the stream of UTRs, spliceosomes, and poly(A) tails is really going to render much of the prose opaque and worthless. Though Lynch makes it clear that details are important, to keep the size of the book down he didn't elucidate what splicing in genetics means and why it's important. Much of the background information is assumed, so if you don't have that under your belt the exposition is worthless. Labels: Genetics
Thursday, November 15, 2007
Mary Murphy of The Jacques Barzun Centennial sent me this link to a video of Jacques Barzun accepting an award recently (large file). He talks about his great-grandmother who would talk about events in her life when he was young. She was born in 1830.
Labels: Barzun
Wednesday, November 14, 2007
With AbeBooks and access to massive university libraries, what's the point of visiting a physical book store? Well, presentation. With online stores and university stacks the search process is rather narrow and focused. You find extremely topical texts with laser-like specificity. But this also means that you won't stumble upon a book which is just outside your search arc; a text whose topicality is somewhat outside of the subject-space which you are exploring, but nevertheless extremely relevant to many of your concerns and interests.
Labels: culture
Tuesday, November 13, 2007
For several years I've been suggesting that people should be relatively unconcerned by the rise of the evangelical Christian counter-culture, and in particular its more ambitious projects, such as Patrick Henry College. My rationale was primarily one based on American history and the experience of Christian anti-modernists with founding institutions to battle back against the de-sectarianization of earlier redoubts. For example, Harvard was founded to train Calvinist ministers. Princeton was founded to train Calvinist ministers after Harvard was suborned from within (it became a stronghold of Unitarianism before its sectarian aspect disappeared). Eventually Wheaton became the Harvard of American evangelicalism. The disquiet over the non-renewal of the contract of a faculty member who was converting to Roman Catholicism suggests to me that the cracks of ecumenicalism are looming on the horizon.
But that's just the American evidence. I think we can increase the sample space from the founding of Christianity, as well as look at other nations. Reading about the Reformation recently I noted again that to engage in full takeover of a society Protestants had to capture the elite, and especially the monarch or potentate. France and the Austrian lands of Germany were initially strongly influenced by the Protestant Reformation, and parity was achieved at least at the level of the nobility. But over time the Catholic monarch forced religious conformity. In places like Holland the small Protestant minority were highly motivated, and without a powerful monarch they were able to engage in full takeover of the society. In Scandinavia and England the change occurred by fiat from on high (Scotland might be an exception to the rule, but its monarchy was particularly weak during this period and the nobles dictated the religion of the young future king James). These "magisterial" Protestants were in many ways quite traditional, and as evidenced by Martin Luther's screed written against the peasants who rebelled against their lords in 1525. They were willing to aid and abet the powers that be and violate the spirit of their original dissent from the central authority of the papacy. On the other hand there were dissenters, radical Protestants, who wished to reorder society through their own interpretation of scripture. The Munster Rebellion is the most antimonian manifestation of this tendency. These attempts to purify the society failed and most radical Protestants accepted that they were the Elect and that the culture at large was going to be outside of salvation. Though mainstream Calvinism is popular among American evangelicals, it is from the radical Reformation that anti-modernist Protestanta derive their true energy and which they most resemble. Though some groups, such as the Jehovah's Witness, have stayed true to the separatist vision, of late some evangelical Protestants have attempted to refashion the broader culture in their own image. Obviously I think they are bound to fail. The attempt to fuse radical Protestantism with the City of Man always results in the latter consuming the former, just as Christian Rock or Rap seems second-hand and derivative. The utopian streak derived from primitive Christianity can have no truck with the amoral and pragmatic necessities of the world (the Pope who was no longer a Prince became a far more luminous spiritual figure). Many radical Protestants look back to the Christian Church before it was championed by the Roman Empire, and suggest that it was the Empire which converted the Church and not the reverse. But of course that early Church's purity was enabled by the fact that it was a minority sect which self-selected its members for their devotion to a separatist quasi-state within the Roman Empire. Any attempts to turn the Roman Empire into a Christian utopia would have foundered on the reality that the institutional structures and purity of belief suitable for a separatist subculture are impractical for a universal political dispensation. Labels: Religion
Monday, November 12, 2007
In an interesting story on the relationship between teen delinquency and sex (long story short: people who concluded early sex caused delinquency unsurprisingly failed to control for genetics and were led astray) I saw this little bit:
A recent study by Scottish researchers asked whether the higher IQs seen in breast-fed children are the result of the breast milk they got or some other factor. By comparing the IQs of sibling pairs in which one was breast-fed and the other not, it found that breast milk is irrelevant to IQ and that the mother's IQ explains both the decision to breast-feed and her children's IQ.Now, this is interesting in light of the recent study claiming to find a gene-environment interaction between breast-feeding and a particular gene. The source for the claim that breast-feeding has no effect on IQ is here. I went back and looked at the recent paper's attempts at controlling for maternal IQ. Statstically, this is not a difficult thing to do-- a linear regression of child IQ on maternal IQ, breast feeding status and genotype can easily be compared with a model that includes a breast feeding staus X genotype interaction. The authors don't do this standard analysis, however--they only include a cryptic note explaining that there is no significant "interaction" between the SNP in question and maternal IQ. It's not the interaction term that's interesting, of course; it's whether the marginal effect of maternal IQ removes their already tenuous claims of an interaction between breast feeding and genotype. One gets the distinct feeling that some unfavorable results are being swept under the rug. Combine this, plus the study above, then add your prior probability that by genotyping two (2!) SNPs in the entire genome you'll find a real gene-environment interaction, and, well, it's not a stretch to say the authors haven't quite demonstrated what they think they have. Labels: Genetics, IQ, Statistics
In DNA Era, Worries About Revival of Prejudice by NYT genetics reporter Amy Harmon is a frank and sensitive look at the burgeoning implications of genetic science to our political and social landscape.
Nothing quite like this article has ever really appeared in the press. The underlying message is that the biological information environment is changing rapidly and if we don't start opening up the tightly monitored public forum for it right now, we are endangering our ability to handle its potential revelations with any sort of real preparedness or rationality. We, as a civilization, can't just keep silencing and punishing everyone who broaches these topics in a way that challenges our hopes and visions about human equality. The result is to shut down the discussion completely and disarm ourselves to ideas that are most likely - to some degree - correct. I appear in this article. The quote is a tiny part of many emails and phonecalls I shared with the reporter in which I stressed that the political implications of genetic differences are still open. I urged that liberals and people of all ethnic groups stake out a territory right now, so the rug doesn't get pulled out from under them. I urged progressives to stop predicating their ideas of justice so religiously on empirical matters which might very well get falsified (leaving the door wide open for rival ideologies). When they do this, open talk or diverse public opinions about genetic differences will not evoke the same level of political threat. Ideally it would be irrelevant. The time for taboos on this topic needs to end. It needs to end because these are issues we, as a diverse world and society, need to discuss and debate openly and fairly, in order to prepare for and accommodate our natural differences as human beings. And for new readers coming in through the Times, my defense of James Watson mentioned by Harmon, James Watson Tells the Inconvenient Truth: Faces the Consequences, is here. Labels: human biodiversity, New York Times
Sunday, November 11, 2007
Engineers are not terrorists, rather, the inverse. At least in some circumstances. Tyler Cowen points me to a new paper, Engineers of the jihad:
We find that graduates from subjects such as science, engineering, and medicine are strongly overrepresented among Islamist movements in the Muslim world, though not among the extremist Islamic groups which have emerged in Western countries more recently. We also find that engineers alone are strongly over-represented among graduates in violent groups in both realms. This is all the more puzzling for engineers are virtually absent from left-wing violent extremists and only present rather than over-represented among right-wing extremists. We consider four hypotheses that could explain this pattern. Is the engineers' prominence among violent Islamists an accident of history amplified through network links, or do their technical skills make them attractive recruits? Do engineers have a 'mindset' that makes them a particularly good match for Islamism, or is their vigorous radicalization explained by the social conditions they endured in Islamic countries? We argue that the interaction between the last two causes is the most plausible explanation of our findings, casting a new light on the sources of Islamic extremism and grounding macro theories of radicalization in a micro-level perspective. My own working model is that engineers (and quantitative scientists) tend to go crazy because their mental outlook is relatively rigid. You don't want to be that creative if you're an applied scientist, you need to take the truths of science as givens and derive practical results. The same tendency can result in a naive fundamentalist outlook when the truths of religion are taken as givens. Additionally, it seems to me a sociological reality that aspirant sub-elites are also the best recruits due to their resentments against an "unjust" order (their talent running up against the fact that they lack culture in the snobby sense as well as connections to leverage their professional competence maximally). The interesting point is that Islamic radicals in Western countries don't fit this profile. I suspect that they can be best modeled as a more conventional class/ethnic nationalism dynamic. Related: Nerds are Nuts. Labels: culture
Economists Oded Galor of Brown and Omer Moav of Hebrew U. argue in a new paper that the Agricultural Revolution created longer lifespans. A simple version of their model goes like this:
Agriculture-->Disease-->Somatic Investment in stronger bodies-->Longer lifespans once things settle down. This result hoists Jared Diamond on his own petard: If the Agricultural Revolution really did make life worse (as he frequently argues), then the forces of evolution would have noticed that fact and reacted in some way. Galor and Moav argue that evolution would respond by building stronger bodies in high-disease environments, and the result would be longer lifespans once those dangers of disease recede in the modern world. More importantly, Galor and Moav argue that we're still living through the Agricultural Revolution: Groups that went agricultural early on went thorough bigger genetic changes. That means that early agriculture should cause longer lifespans. An interesting theory, but what's the evidence? They use Putterman's new estimates of the year that countries went agricultural, control for a lot of the usual suspects, and find this:
A couple of facts about the agricultural transition: The differences across countries are big, according to Putterman: The average country went agricultural about 4500 years ago (mean and median within a couple of hundred years). Standard deviation: 2400 years. 10th percentile: 1500 years ago (mostly sub-Saharan countries, plus some New World countries) 90th percentile: 8000 years ago (Eastern and Southern European countries--the Middle East was earlier). So the cross-country differences appear big enough to be evolutionarily important a priori. But back to Galor and Moav's big result: Almost 2 years of life for a thousand years of agriculture: Maybe that number will become a new stylized fact in the economics-and-evolution literature. It'll be interesting to see if this result comes up in political debates over health care reform.....
Saturday, November 10, 2007
There was recently widespread publicity in Britain and even internationally for the tragic case of Jean Gambell, who (according to the reports) was locked up as a lunatic at the age of 15 after being falsely accused of theft, and then 'lost in the system' until her family rediscovered her shortly before her death at the age of 85. Cue for much moralising over our predecessors' inhumanity and willingness to lock people up on the most trivial grounds.
As this article in the London Times reveals, the true story is more complex and nuanced. It turns out that Jean was one of a large and impoverished family, who aroused the concern of the local social services (or whatever they were called in those days). In 1937 she was found by the authorities to be a 'feeble-minded person' who was 'neglected and subjected to emotional deprivation', and committed to a mental institution with the consent of her father. (Her mother was herself already institutionalised.) Some years later she was released on licence to work at a doctor's surgery, but recalled to the institution after an allegation of theft (which later turned out to be false). She spent the rest of her life in various institutions, but contrary to the earlier press reports she was well looked after and had regular contacts with her younger siblings until some time in the 1980s. Then her mental home was closed, and contact was lost until a chance discovery earlier this year. It is still a desperately sad story, but it is not obvious, on the evidence of the article, whether the authorities acted wrongly in regarding Jean as in need of shelter and supervision. This will probably not prevent the case entering the mythology of mental health care.
Friday, November 09, 2007
Tyler Cowen points and interest working paper, What's Love Got To Do With It?
Parental Involvement and Spouse Choice in Urban India: ...when parents are involved in mate choice, sons are significantly less likely to marry college-educated women and women engaged in the labor force, after controlling for individual and family characteristics. I show that these effects are driven, at least in part, by parental preferences and cannot be entirely attributed to correlation between arranged marriages and unobserved characteristics or preferences..... To cut the chase the paper suggests that parents prefer that their sons marry someone who is in a relatively weak bargaining position in terms of allocation of economic resources in the future. The rationale from a parental perspective is that as they age they will depend upon their son's household to provide financial support when their own earning power diminishes (i.e., familial social security). Though a daughter-in-law who is an economically productive professional increases the resources which might be allocated toward her in-laws, the concomitant independence is judged to more likely result in resistance to intergenerational transfers of wealth. The author focuses upon upper-middle class families in Bombay in her survey, as presumably they are are the cultural "cutting edge" and more likely to manifest the noticeable shift toward "love matches" within Indian society. She notes that arranged marriages are ubiquitous amongst the lower classes and less economically advanced. But I have to wonder, how recent is the ubiquity of this particular cultural practice within South Asia? A survey of the ethnographic literature will show that within the past few centuries (even within the past century) "elite emulation" has been a noticeable dynamic which has transformed Indian society. Within the Hindu context there has also been a great deal of "Sanskritization," an attempt to shift away from local customs and tradition and conform to upper caste practices which often have a North Indian provenance. For example, in South India the Nair caste shifted away from their customary matrilineal & matrifocal systems of inheritance and residence only within the past few centuries (the literature makes clear that other Hindu groups found Nair practices abhorrent). The custom of dowry is often considered part and parcel of Indian culture, but there is a good deal of evidence that many non-upper caste groups have only begun to practice it in the 20th century, prior to which they adhered to brideprice if they engaged in wealth transfer at all. Similar shifts have occurred in terms of the consumption of beef and meat-eating in general. In the data above arranged marriage is associated with multi-generational extended family households. These marriages are seen as an alliance between families and a way to advance material interests through connections with other lineages of similar power and status, at least on the conscious level (note that the data above implies that the parents are also behaving as rational actors maximizing their own security even if it reduces the greater glory of the family). From a Western perspective the dynamics operant upon European elites until recently serve as a good analogy. Napoleon married the daughter of the Hapsburg emperor because he perceived that the best way for a parvenu soldier to secure his status among the royal families of Europe was to marry a member of one of the oldest aristocratic lineages of note. In return the Austro-Hungarian empire had hope that they'd won a measure of peace and security by cementing an alliance with the conqueror of much of the continent. Though such world-historical implications are not operative in the typical arranged marriage, quite often attention to material wealth, status and the positives & negatives of the possible inter-familial association are considered in great detail. These are the explicit raison de'tre of the marriage. With that in mind I think that when looking at arranged marriages in the long-view it seems that the relatively rigid form with little input from the principals must have emerged relatively recently in human evolutionary history; likely within the last 10,000 years due to the rise of "civilization" and the accumulation of power, status and wealth among specific lineages within a locale. In many societies, such as early modern Europe and Japan, an arranged marriage was a sign that the familial context was elite. For the typical peasant the pool of potential partners was likely small because of constraints of geography, a man and woman were economic partners in maintaining a lifestyle above the margins of subsistence. Norms and values promoted by elites are certainly extant within the literature which captures the Zeitgeist of any particular age, but until humanity broke out of the Malthusian Trap these values were irrelevant for the overwhelming majority of the population. The current situation in Indian society, where there are competing cultural ideals and the economic wherewithal to engage in a range of choices, is atypical and characteristic of a culture in transition. A wave of elite emulation by the lower orders within Indian society within the past few decades is manifest evidence of some level of economic prosperity, after all dowries are a major burden, while curtailing consumption of potential sources of protein due to concerns about pollution and loss of status also suggest a robust enough diet where such choices are an option (there's actually a good deal of evidence that in some regions of India Hindus converted to Islam simply because they had already lost caste by the consumption of polluting foods, either inadvertently or under duress). The particular dynamics fleshed out above might also not be the norm in the historical scale, as mass adoption of the practice below the highest elites might be relatively recent (social security would have been less of a concern for the extremely elite in most cultures who were safeguarded by rents). Prior to the Reformation the Catholic Church had generally increased the choice that potential spouses had in regards to their partners and also banned moderately consanguineous relationships (e.g., first cousins). After the Reformation elite lineages began to engage in cousin marriage, often as a way of consolidating property, concentrating wealth and cementing familial bonds. There was also marked tendency toward increased parental control over the marriages of their offspring. These dynamics show that the pent up tendency was there, only constrained by the fiat of the Catholic Church (marriage was a sacrament under religious control, and marriages which produced illegitimate issue could be useless in terms of perpetuating the family legacy). Yet neither of these are major issues for most of Protestant Europe as cultural norms have evolved and shifted naturally. In the case of India as the upper and upper-middle classes continue to grow in wealth it seems likely that norms will naturally evolve away from parental control toward individual choice. As the elites abandon practices such as arranged marriage and dowry once their group-level utility decreases one assumes that the lower orders will emulate them quickly, in particular since the gains from some of the practices (e.g., consolidation of wealth via arranged marriage) are minimal and the losses from others are more significant (e.g., debts incurred due to dowries or more marginal nutrition because of constrainment of dietary sources of protein). An interesting final point is that the paper above notes that there is some positive correlation between arranged marriage and caste, religious and ethnic endogamy vis-a-vis a love marriage, while there is some disassortative mating along the axis of educational attainment (i.e., sons with a college education are less likely to marry a woman of the same educational status). I have often wondered as to the effect of the changes in the cultural environment in regards to assortative mating and the heritability of particular traits (assortative mating often increases within population heritability). The classic example is the fact that most female physicists are married to other physicists. This is a function of the lopsided sex ratio, but in the early 20th century obviously this wouldn't have been a nearly irrelevant fact because there were hardly any female physics Ph.D.s. A pooling of extremely intelligent individuals at elite universities or graduate schools from which they select their partners is a radical change; after all, higher education for women is a relatively new phenomenon. One assumes that the likelihood is that most men with higher educations would find a wife from the same social order in the past, but because of within family variation in propensities I assume that the assortative mating was less pronounced (fathers & brothers are imperfect proxies). An economist may see in love marriages a more efficient allocation of human capital, but I can't but help wonder as to the possibility that the enormous sample space of mates of like mind and character is a more efficient across population genetic architecture (at least for the purposes of increasing the variance of trait value). Note: The popularity of tales of tragic love attest to the recent origin and shallow extent of arranged marriage where the offspring have little choice. The lack of evolution of the underlying psychology suggests little selective pressure. Labels: Evolutionary Psychology  Alex Palazzo has a little post on the "brainbow mouse", created using some of the transgenic methods mentioned by amenestic in a post a while back. Each individual neuron in a given mouse brain expresses a random combination of fluorescent proteins, allowing analysis with the naked eye. Pretty amazing stuff. Alex Palazzo has a little post on the "brainbow mouse", created using some of the transgenic methods mentioned by amenestic in a post a while back. Each individual neuron in a given mouse brain expresses a random combination of fluorescent proteins, allowing analysis with the naked eye. Pretty amazing stuff.Labels: Genetic Engineering, Neuroscience
Hm. I wonder if Finn-baiting might not be so safe. See here:
Although gun violence is very rare in Finland, the country has the highest rate of firearm ownership in Europe and the third highest in the world, behind only the United States and Yemen. Why do so many Finns own firearms? Since when was Finland in Western Europe? Labels: Finn baiting
Just curious. I have a rough intuition. So I went to Porn stars by nationality on Wikipedia. I clicked the entries and tallied up the number of porn stars. I excluded English speaking countries since I figure that the listing would be biased that way because this is an English language encyclopedia. I created a "porn star index" by dividing the number of porn stars by population and then renormalized using the entry with the smallest value.
Labels: porn
Thursday, November 08, 2007
I've been reading a bit of the literature of the cognitive science of religion, as well as a good deal of material on the Reformation (for the former, see In Gods We Trust and Religion Explained). Trying to make heads or tails of the dynamics which we see in the world around us isn't easy (at least for me). One of the major issues which crops up when psychologists explore how individuals model their gods is a dichotomy between a reflective conception and a reflexive intuition. People can give rough sketches of their theology of choice, but when prompted with little warning to narrate their god acting upon the world the implied characteristics tend to differ sharply from the formula which they earlier provided. The implication is that in parallel with a conscious god-model adhered to for the purposes of group identity most humans have an implicit subconscious model which they use in day to day cognitive processes. Some workers posit that this dual nature of god-concepts explains the tension between elite religion and folk religion, the high church and the low. The process of sect formation and religious revivalism may be the natural byproduct of this tension, as the masses attempt to draw away from elite attempts to shoe-horn theism into a hyper-rational and abstract system which doesn't satisfy their psychological needs and intuitions (in the American context this would be the switch from liberal Protestantism to evangelical Protestantism; though the latter is more orthodox in its theology, it is still considerably more penetrable than some of the abstruse material generated by modernist icons such as Paul Tillich).
With that, I was interested in some of the facts relayed in The Protestant Reformation: Beliefs and Practices: The Reformation may eventually have become a popular movement, but it had its origins in the intellectual developments associated with Humanism and the Renaissance. The early reformers were virtually all of them university-educated men. Most of them were trained theologians, but they had also had a solid grounding in classical scholarship and in the techniques of logic and rhetoric.... The "university-educated" portion really jumped out at me. Remember that this was a period when most of the populace was not functionally literate! The Reformation was a world-shaking event. Luther and Calvin and their fellow travelers ushered in a period of communal bloodshed which culminated in the international Thirty Years' War, which many take to be a turning in point Europe's love affair with state sponsored religion (the discontinuity is not so sharp, note the revocation of the Edict of Nantes which postdates the Peace of Westphalia by a generation). Obviously there were other contingent factors which played a role in the Reformation besides the intellectual firepower of men such as Martin Luther. Most people can probably agree that the printing press was a critical catalyst in the emergence of a robust republic of letters which served as the vehicle for a rapid sweep of new ideas across populations. But that catalyst needed a substrate to operate upon, so ideas in and of themselves did matter. I was interested to discover that John Calvin, the hero of the Reformed movement and the god-father of many Christian conservatives, was not a literalist. For example, believed that Genesis was a simplified narrative aimed toward a particular audience. In fact many of the reformers were taken aback by the simplistic reception of their message among the masses; some radicals took to sola scriptura and began to use the Bible as proof text for all elements of their lives. Many of these were the precursors of the Anabaptists, who were persecuted by Lutherans and Calvinists as well as Catholics. Additionally, the sophisticated arguments exposited by the intellectuals were not well understood by the typical enthusiastic convert. At one point one of Luther's followers, Andreas Karlstadt, preached against the Catholic interpretation of the eucharist to a sympathetic crowd, but was expelled a few days later by the same people for not celebrating the eucharist in the "proper" (i.e., Catholic) manner. But to me iconoclasm is the most interesting phenomenon. The destruction of images, sculptures and art-work in general as "idolatry" is very familiar. In both Korea and Brazil radical Protestants have engaged in the destruction of religious imagery of their "idolatrous" opposition within the past few years, and we don't even need to talk about the Bamiyan Buddhas. The reformer Huldrych Zwingli of Zurich was disturbed by the more enthusiastic iconoclasts who were destroying works in his name, and tried to salvage some of the stained glass in his church in vain. His followers were no longer under his control when it came to some questions whose correctness they needed no scholarly guidance on. The most extreme case of iconoclasm in the modern or early modern era is clearly manifest in Islam; Wahhabi radicals have been engaging in the destruction of sacred architecture and sites for several centuries. Though Islam is ostensibly an unadorned monotheism, as a practical matter there is a fair amount of veneration of saints and holy men, particularly around their burial sites. John Calvin was buried in an unmarked grave because his followers were worried about the likelihood that such a site would become one of pilgrimage for those who venerated him. It seems clear that these recurrent manifestations of iconoclasm are natural implicit inversions of the tendency to imbue in objects and places a sacred importance. The rage of iconoclasm and the passion that it elicits issues from the fact that the destroyers understand very well the natural impulse to venerate particular persons and the objects and places which are imbued with their charisma. On the one hand folk religions, whether Catholic or Protestant, Muslim or Hindu, exhibit similar tendencies and manifest the same general motifs. But this ocean of intuitive religious sensibility is periodically roiled by "reformist" tendencies from waves from on high which are able to spread quickly because of their transmission via explicit verbal creeds and arguments. Folk religion is limited in its spatial expanse because of its relationship to objects in the landscape, relics of obscure saints and sacred places of parochial importance. Its roots are deep, but its canopy is narrow. In contrast elite reformist movements are portable bits of data, memes, which are constrained only by the information technology and the necessary lubricant of mobile and literate evangelists. Ergo, the printing press combined with a standing cadre of intellectuals (generalized subsided by the Catholic Church ironically!) enabled the Reformation to explode beyond the control of monarchs bent on strangling it (remember that Henry the VIII was against it before he was for it!). Events such as St. Bartholomew's Day Massacre show the power of these emerging memeplexes to crystallize divisions and coalesce ingroup-outgroup sentiments. But as these movements spread and diffused down the social ladder the tightness and integrity of the myriad memes becomes garbled; nuanced theological arguments reduce down to intuitively tractable maxims such as the destruction of idols. The various currents and tensions working at cross-purposes likely cycle over time and produce a metastable equilibrium. Addendum: Not only did Protestantism emerge as an idea promoted by a small group of intellectuals, its initial successes were among urban or elite segments of the populace. The French Protestants, the Huguenots, were able to hold their own in the face of Catholic persecution for several centuries because of their concentration among the higher orders of society and the critical mass in the cities of particular regions. In Poland, Austria and Hungary at one point the higher nobility seems to have turned predominantly Protestant. In Poland persistent (though weak) pressure from the monarchy combined with the historical circumstance that Protestantism became associated with traditional enemies (Prussia and Sweden) resulted in the re-Catholicization of of the nobility by the 18th century. In Austria the Hapsburgs forced a re-Catholicization through incentive and coercion. In Hungary a Protestant minority remained despite widespread defection, but this was due to the historical coincidence, as the south and east of the country was under Ottoman domination and so beyond the reach of the Counter-Reformation. I bring up these minutiae to show that even though Protestantism as an idea swept many elites, it was generally successful in sinking deep roots only where the apex of the political order favored it for a substantial period of time (England, Scandinavia, the principalities of northern Germany, Geneva, and the Netherlands). Conversely, even if the Reformation did not succeed it often left a lasting impact. The French Protestants who fled in the late 17th century from persecution and forced conversion to Catholicism left a lasting mark across the globe, from South Africa to Berlin to England. Even though the Reformation was never a mass movement in Italy, some of the most radical thinkers were Italian, and shaped the course of movements such Unitarianism in Transylvania. And remember that the most prominent Unitarian of the age, Michael Servetus, was Spanish! Finally, I don't want to emphasize historical contingency too much. During the first decade or so of the Reformation the Hapsburg monarchy was dealing with a Turkish march deep into central Europe. The Ottomans were beaten back from Vienna only in 1529, and for a century and a half afterward they were a persistent drain on the Hapsburg treasury. Some have argued that the Ottoman offensive of the early 16th century was a necessary precondition in giving Martin Luther and other radicals respite from attempts by the center to bring them into line. This is possibly correct, but that does not mean that the Reformation of the early 16th century was a once-in-a-universe phenomenon. With the printing press, the emergence of a larger middle class and the coalescence of proto-nations during the Renaissance it seems that the likelihood for religious discord was high. The Hussite rebellion shows that many of the preconditions were already extant during the late medieval period. A convergence between the explosion of Martin Luther and the Turkish worries of the Holy Roman Emperor might have been fortuitous for the Reformation, but it seems likely that if Suleiman the Magnificent had turned all his attention to Persia in the east any success of stamping out of the heretics would only have delayed the inevitable reckoning with the pent up social pressures and the technology to unleash them. Labels: Religion
Tuesday, November 06, 2007
This is an update on my previous post about hair thickness. In this post-genomic era the precision and data density we gain from more powerful techniques and sharper analytical techniques when it comes to genetic variation is not always supplemented by a concomitant increase in characterization of phenotypic variation. Sometimes it is best to look to older works from the lost age of physical anthropology; from page 63 of Racial Adaptations, the following data:
Area of the cross-section of hair in square millimeters 0.126 African 0.135 Blond European 0.193 Solomon Islander 0.204 Chinese Weight in milligrams of a five-centimeter segment of an average hair 2.10 Brown haired European 2.15 Blond haired European 2.71 African 3.85 Black haired european 4.95 East Asian Volume of five-centimeter segments of three kinds of hair two previous studies had in common 6.30 African 6.70 Blond haired European 10.2 East Asian Weight-to-volume ratio 1:2.3 African 1:2.4 Blond haired European 1:1.2 East Asian Labels: human biodiversity
Monday, November 05, 2007
The current issue of CATO Unbound is about IQ. James Flynn has already put something up, Linda Gottfredson, Stephen Ceci and Eric Turkheimer on deck.
Labels: IQ, Psychology
Read it here.
Update: Eye on DNA has much more. Jason M. adds: In the comments HapMap Jockey Marc again applies the wisdom from p-ter's HapMap How-2 to the latest IQ genes: In the study itself, there were two cohorts: a British cohort and a New Zealand cohort. In both cohorts, presence of the C allele (as either CC or CG) was associated with a hike in IQ by 6.4 and 7.0 points (from around 99-100 to around 106) in the two samples. But those without the C allele (GG) had mean IQs of 99.5 in Britain and 100.3 in New Zealand. Additional props to Rob in the comments at FuturePundit. Labels: Behavior Genetics, IQ
Just a note to all the nerds, Beyond Belief II is complete. Here is a list of speakers. Many familiar faces, but some new ones too. It will be posted at The Science Network when editing is completed.
Sunday, November 04, 2007
Nature has a news piece on vastly improved models for psychology-related phenotypes in model organisms. It's worth a read, keeping in mind James Watson's claim from last year that "the past century was the coming together of chemistry and biology, and this century will be the coming together of psychology and biology".
The story highlights the progress being made in studying the brain the way other organs have been studied for years. And right after I read it, I saw a couple papers that hammer the story home. First, Molecular Adaptations Underlying Susceptibility and Resistance to Social Defeat in Brain Reward Regions, which shows that genetically identical mice can be divided into two groups based on how they respond to social defeat (from the paper: "An episode of social defeat is accomplished by forcing a mouse to intrude into the space territorialized by a larger mouse of a more aggressive genetic strain, leading to an agonistic encounter that ultimately results in intruder subordination.") and identifies particular molecules whose expression levels differentiate the two, mostly involved in a specific signaling pathway that goes through a protein encoded by BNDF (brain-derived neurotrophic factor). How could genetically identical mouse strains react so differently to stress? The authors don't really know, offering only this: Such examples of phenotypic variability in inbred mice have always been attributed to environmental influences that are difficult to control and measure, such as variations in prenatal and postnatal development and early dominance hierarchies ([Peaston and Whitelaw, 2006] and [Wong et al., 2005]). However, experiments performed on inbred mice raised in strictly defined environments have shown that up to 80% of random variability in quantitative traits (e.g., body weight) are unrelated to genetic and environmental influences (Gartner, 1990). This third component to natural variation is thought to maintain Gaussian distributions of biological variables independent of environmental influences and sequence constraints and is now attributed to chromatin remodeling events such as histone acetylation or methylation.So perhaps it's just random chance? In humans, however, there is genetic variation in the genes these authors identify, including a non-synonymous (Met->Val) polymorphism in Bndf that affects the expression level of the gene. The authors are able to test this polymorphism in their framework: We show here that while Val/Val and Met/Met mice showed comparable behavior on baseline measures of emotionality, Met/Met mice displayed a striking Unsusceptible [to depression following social defeat] phenotype in the social defeat paradigm, which was associated with a ~50% reduction in levels of BDNF proteinIt's quite possible, then, that this polymorphism plays an important role in how humans respond to certain social situations, though this remains to be seen. The other paper that caught my eye was on the results of performing brain MRIs on people from the general population. I never would have thought to check if individuals had had random small strokes, but that's what they find: Asymptomatic brain infarcts were present in 145 persons (7.2%). Among findings other than infarcts, cerebral aneurysms (1.8%) and benign primary tumors (1.6%), mainly meningiomas, were the most frequent. The prevalence of asymptomatic brain infarcts and meningiomas increased with age, as did the volume of white-matter lesions, whereas aneurysms showed no age-related increase in prevalence.So around 10% of individuals over 50 are walking around with some sort of brain damage. I suppose there are a couple ways to respond to that information-- either you adapt your view of what a normal brain is, or you become suspicious of anyone above a certain age.
Statistical Modeling, Causal Inference, and Social Science has an interesting post where they present two charts; one displays average religious attendance vs. average income and another within-state correlation of religious attendance vs, average income. The red data points show states where George W. Bush won the popular vote in 2004 and blue John Kerry. Two conclusions:
There is an important caveat here: religious attendance is not a perfect proxy for religiosity. In some cultural contexts religious affiliation and attendance are critical social markers. You can see data from many Catholic countries which attests to this, disaffiliation is very strong among the lower and working classes due to anti-clerical socialist movements as well as the association between the powerful & the Roman Catholic elites. But this does not necessarily mean that there is no religious sentiment among the non-affiliated population, for example, in Chile the lower classes who have traditionally been apathetic to Roman Catholicism are converting wholesale to evangelical & charismatic Protestant groups. This manifests the division between denominations and sects. The former exist at low tension with society, make modest demands, and are avenues toward respectability. In the United States Episcopalianism is a classic denomination. Sects on the other hand tend to exist at some remove from the rest of the population & make significant demands on adherents. The Assemblies of God would be a sect. In general the history of most religious groups in the United States exhibits the transition from sect to denomination. Methodism is a case in point; initially an evangelical revival movement derived from Anglicanism it is now a respectable mainline denomination. Some religious groups manifest several tendencies; Roman Catholicism for example has several sectarian movements which nevertheless remain under the umbrella of the Church. How does this work in relation to the data we have above? From what I know in the American South religion still exists as a social marker. Episcopalians are at the top, Presbyterians below them, then Methodists, then Baptists, and finally various sects with charismatic tendencies. Presidential candidate John Edwards illustrates this; raised in a working class Baptist family he is now a member of the United Methodist church, which is more in keeping with both his rise in the class system as well as his more liberal religious inclinations and politics. What about the rest of the country? It seems likely that in many regions of the United States association with religious institutions no longer serve as necessary accessories in the lives of public citizens. At the commanding heights of public life religion still seems rather important, note the overwhelming avowed affiliation of United States members of Congress. On the margins religious affiliation probably matters even outside of the South, but the affect is weak enough that the often tepid and skeptical inclinations of Western cultural elites has resulted in disaffiliation. For lower status individuals the small absolute marginal return on sectarian affiliation is still high enough that they will still affiliate. Consider new Korean immigrants who do not speak English well; the local Korean Presbyterian church likely serves a very practical role in their lives in terms of connecting them to a community in which they are comfortable and which returns tangible practical benefits. In the South non-affiliation is atypical enough that the negative consequences are strong enough that elites still make sure to find a "church home" so as to embed themselves in a religious institution. Labels: Religion
Saturday, November 03, 2007
Thursday, November 01, 2007
 A few weeks ago I speculated that the EDAR gene was responsible for variation in hair form in regards to curly vs. straight. I based this on the distribution of polymorphisms and the variation of the phenotype geographically. I was wrong. Rather, it is responsible for variation in thickness of the hair follicle. A Thick Head of Hair Is in the Genes: A few weeks ago I speculated that the EDAR gene was responsible for variation in hair form in regards to curly vs. straight. I based this on the distribution of polymorphisms and the variation of the phenotype geographically. I was wrong. Rather, it is responsible for variation in thickness of the hair follicle. A Thick Head of Hair Is in the Genes:...Geneticists at the University of Tokyo and several other institutions in Japan, Thailand, and Indonesia have now used the HapMap to explore why Japanese and Chinese people have thick hair: The cross-sectional area of East Asian hair fibers averages about 30% larger than that of Africans and 50% larger than that of Europeans. The researchers specifically rejected the correspondence of a particular genotype on this locus to phenotypic curliness or straightness. Don't pay attention to the adaptive explanations, the literature in this area offers cold climate as the explanation for nearly all derived East Asian features. EDAR is a major nexus for a lot of developmental action. It seems that wearing a fur cap of some sort would be better insulation than thicker hair! What we do know is according to haplotter the whole region around EDAR has been slammed by selection, SLC5A7, LOC402097, SULT1C1, SULT1C2, GCC2, LIMS1, RANBP2, FLJ32745 and finally, EDAR (just type EDAR into the "gene name" text box). Labels: Genetics |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||



