|
Thursday, July 31, 2008
In yesterday's New York Times article, David Goldstein makes sense: he says "We've looked for common variants in schizophrenia and get almost nothing. This means natural selection has done a really good job of purging them away, and we're left with rare variants, a constant flow of them, as the principal driver of the disease."
Which is what any reasonable person thought a long time ago: the common disease-common variant notion never made much sense for a syndrome with a large impact on fitness. That genetic heterogeneity does not make drug development easier: even if the mutations cluster in certain pathways, reactivating a broken pathway may still require mutation-specific methods, which would sure take the profit out of drug development. But the most interesting point in the article is Stefansson's statement - "I would have thought the brain was a luxury organ when it comes to reproductive success." That's a weird thing to say. For one thing we known damn well that schiz strongly impacts fitness, even in contemporary society: the affected families dwindle away, which interferes with genetic studies. More than that, does he really believe that being insane had no effect on reproductive success back in the Malthusian past? It's hard to find a place more Malthusian than Iceland: does he think that crazy hardscrabble farmers did just as well as sane ones? Does he think that lunatics were just as likely to become godir and hornswoggle the neighbors out of their land? The brain burns out 20% of our calories: does he think that could continue long under natural selection if there wasn't a big payoff? The answer is that he _does_ think all those absurd things: he doesn't believe in ongoing natural selection in humans, particularly above the neck. I wonder why - but once we sequence him, maybe we'll know. Labels: Genetics
Wednesday, July 30, 2008
Nature has published a couple papers reporting (using partially overlapping samples) associations between rare recurrent microdeletions and schizophrenia. The paper from Deocde Genetics hits an evolutionary angle from the first sentences:
Reduced fecundity, associated with severe mental disorders, places negative selection pressure on risk alleles and may explain, in part, why common variants have not been found that confer risk of disorders such as autism, schizophrenia and mental retardation. Thus, rare variants may account for a larger fraction of the overall genetic risk than previously assumed.Rare variants often have much larger phenotypic effects than more common ones; this case is no different: All three deletions, at 1q21.1, 15q11.2 and 15q13.3, significantly associate with schizophrenia and psychosis in the combined sample with high odds ratio (OR) (p = 2.9x10e-5, OR = 14.83; p = 6.0x10e-4, OR = 2.73; and p = 5.3x10e-4, OR = 11.54, respectively)Note that despite these massive odds ratios, these deletions explain a tiny fraction of all cases of schizophrenia due the their extremely low frequency. Still, these genomic regions seem like important areas for following up via functional studies or searching for more common polymorphisms.
Tyler points to a new story in The New York Times highlighting discoveries about the Antikythera mechanism:
The new findings, reported Wednesday in the journal Nature, also suggested that the mechanism's concept originated in the colonies of Corinth, possibly Syracuse, in Sicily. The scientists said this implied a likely connection with the great Archimedes. My explanation: the ancients had scientists and technologists, but they did not have Science and Technology. In other words, science and technology as we understand it today in the age of scientific industry is a cultural complex which has attained critical mass and is self-perpetuating. One does not need to manifest the brilliance of Isaac Newton to stand upon his shoulders, the sociocultural framework takes Newtonianism as a given. There were scientists in ancient Greece, in the Islamic world, China, India, etc., of various sorts. But these people lacked a cultural framework in terms of a critical mass of numbers which arose in the West sometime between 1600 and 1900 as a cumulative process.* This is not to say that the "knowledge based" economy is a function of the modern West, it is not. The ancient Greeks had lawyers, doctors and philosophers. So did many other civilizations at various points in history. Legal frameworks, as an example, are essential for complex society, but it also seems to be that they arise necessarily from mass societies of a particular threshold of complexity. The mass societies of the post-Neolithic world straining against the bounds of the Malthusian trap were not barbaric; but they were not mass consumer societies. While I do not believe that science & technology as I am conceiving of them in this post were necessary or sufficient to drive the productivity gains which are required for existence outside of the Malthusian trap,** I suspect that they will be necessary to perpetuate said society into the indefinite future. Science & technology are not hallmarks of civilization, but they necessities of continued affluence. * That cultural complex's emergence might be contingent upon a host of parameters. For example, the printing press, the unity imposed by Latin as a common language for western European intellectuals, the lack of a unified ideology to suppress diversity of thought (remember that the Reformation broke the Church's power to stifle new currents in Protestant Europe, while Protestant high priests likewise had no power in Catholic Europe), etc. ** This is not to say that I don't think technology was not necessary or essential for the massive productivity gains, but the scientific-industrial-complex which we know and love (I hope!) today didn't coalesce into its full form until the past century or so, though I do believe its origins can be traced back to the 17th century. Labels: culture
Yesterday I finally finished Kenneth Pomeranz's The Great Divergence: China, Europe, and the Making of the Modern World Economy. This was no easy read, even at only ~300 pages. Will Ambrosini characterized Greg Clark's Farewell to Alms as a book length response to The Great Divergence, and I can see where he is coming from. Contra Clark and the dominant consensus in economic history Pomeranz marshals the evidence which suggests that China & Japan were basically as wealthy as western Europe during the 18th century, and that many of the presumed necessary preconditions for the economic liftoff which we term the Industrial Revolution after the fact also held for eastern Eurasia. But Pomeranz has his own solution for why the West, and in particular England, rose to prominence when it did: the location of coal near the core economic regions combined with the massive input of land due to the opening up of the New World.
Those of us who are a bit younger no doubt encountered a fair amount of revisionist history. Instead of a "Whiggish" vision where civilization ascended in a linear fashion from Greece, to Rome, to the Middle Ages and onto the culmination of the Anglo-American culture, we were reminded that during the medieval period the West was much less than the rest, while even during the height of Imperial Rome Han China flourished with relative parity. Instead of these impressionistic generalizations the central figures in economic history, such as Angus Madison, emphasize that the revisionism might have been true in economic terms in 1000, but not by 1500. In the year 1000 western Europe was a rather poor region compared to the Islamic societies or China. By 1500 the conventional wisdom seems to be that much of western Europe was at least at parity, and likely one of the wealthier regions of the world on a per capita basis, if not the wealthiest. Because of the raw size of China and India Asia was still the economic center of the world, but by 1500 Europe, in particular its west, was no longer marginal. Between 1500 and 1800 western Europe might have been the wealthiest and most powerful region of the world on a per unit basis, but non-European powers could still operate on the same playing field, as evidenced by the need for European powers such as Britain and France to curry favor with Asian potentates to obtain trading rights. During the 19th century this changed; what was a difference in wealth on the margins transformed into one characterized by a qualitative chasm (symbolized by the maxim machine gun). The Great Divergence tries to throw some cold water on the metrics used to make the case that Europe was already wealthier, and more well positioned institutionally, to achieve liftoff at the end of the 18th century. It is obvious that Pomeranz is correct when he seems to imply that there are apples to oranges comparisons; much of eastern Europe remained quite poor, so it was not Europe as a whole which was wealthy (there were even extremely large variations within nations, such as the Rhineland vs. eastern Prussia). Additionally, China was characterized by a great deal of the regionalism so that the most dynamic subunits of that civilization are more usefully compared to with France, Britain and the Low Countries, the most advanced subunits of the greater European economic region. All that being said, only someone who is rather well versed in the literature in economic history could appreciate much of the material that Pomeranz references throughout the narration; to a great extent The Great Divergence was argument by filibuster. Those who are familiar with the full body of the literature may be able to evaluate the power of the argument, but for those of us who are relatively uninformed we are simply confronted with an undifferentiated mass of data. Some of the data and insight was very useful. For example, cultural historians often attempt to claim that one reason that the Chinese imported so little from European nations was because of their own superior attitude. In other words, the dynamics we observe were driven by variations in taste. This is an entirely plausible argument, and one which I accepted. Entire swaths of scholarship are based for example on the contempt which the Chinese government directed at European trade delegations and their wares. Pomeranz makes the argument that the imbalance in trade was a function of the fact that China was re-monetizing their economy with silver, and Europeans were there to provide silver through the opening of New World mines. The difference in value of silver in China and the rest of the world naturally resulted in an arbitrage opportunity so that the Middle Kingdom was a magnet for this metal; naturally the Chinese had to pay for silver with products, ergo, the export in finished goods such as porcelain. This economic argument does not negate the cultural explanation, one might admit that cultural and economic trends often dovetail or play off each other synergistically, but this sort of datum is gold in trying to understand how history plays out. With that, I'll open up the comments to those who know the literature and what their opinions might be.
Tuesday, July 29, 2008
Brooks sets out to share his wisdom on the root causes of America's past success and why we're faltering of late. He writes:
As Claudia Goldin and Lawrence Katz describe in their book, "The Race Between Education and Technology," America's educational progress was amazingly steady over those decades, and the U.S. opened up a gigantic global lead. Educational levels were rising across the industrialized world, but the U.S. had at least a 35-year advantage on most of Europe. In 1950, no European country enrolled 30 percent of its older teens in full-time secondary school. In the U.S., 70 percent of older teens were in school. What could have happened in the 1960s that could, by 1970, lead to the cessation of the educational gains we had made over the 50 - 75 years? Has anyone looked at Senator Ted Kennedy's handiwork? Well, Brooks certainly doesn't even entertain the notion that the demographic nature of the US today is different from what it was during most the century preceding the 1965 Immigration Reform Act. Moreover, during the sustained periods of immigration restriction the cultural focus was squarely on assimilation and unlike today, educational resources were not squandered on celebrating diversity, rather they were targeted towards moving all children along a common cultural vector. Goldin and Katz describe a race between technology and education. The pace of technological change has been surprisingly steady. In periods when educational progress outpaces this change, inequality narrows. The market is flooded with skilled workers, so their wages rise modestly. In periods, like the current one, when educational progress lags behind technological change, inequality widens. The relatively few skilled workers command higher prices, while the many unskilled ones have little bargaining power. Having an immigration policy which pulls in tens of millions of 6th grade educated, Spanish-speaking immigrants is a policy that creates inequality. Goldin and Katz would do well to control for immigrant status, legal and illegal, in the ranks of the low skilled. The meticulous research of Goldin and Katz is complemented by a report from James Heckman of the University of Chicago. Using his own research, Heckman also concludes that high school graduation rates peaked in the U.S. in the late 1960s, at about 80 percent. Since then they have declined. Again, demography matters. When we celebrate diversity and when we hold all cultures to be equal then we discount the importance that cultural practices, traditions and views have on real world factors, like education and economic productivity. Heckman notes that "some children" benefit from family practices that promote human capital development, but that many don't. I'm willing to wager that racial and cultural factors correlate to a good deal of this disparity. It's not globalization or immigration or computers per se that widen inequality. It's the skills gap. Boosting educational attainment at the bottom is more promising than trying to reorganize the global economy. It's fantasy to posit that the skills gap is independent of group measures of human capital stock. ParaPundit shows the dismal embrace of higher education by Hispanics even after 4 generations in the US. America rose because it got more out of its own people than other nations. That stopped in 1970. There are two things wrong with this claim. First, measuring what a country gets from it's people is simply another way of referencing the concept of productivity and US productivity increases didn't stop in 1970. In fact, from 1995-2005 the US experienced a 2.35% annual rate of productivity growth, which was only exceeded by the rates experienced in Iceland, Finland and Sweden. We're clearly able to "get more" out of our citizens. Brooks' conflates educational attainment in a nation with productivity growth. Clearly, some segments of our population excel at educational attainment while others groups stumble. Secondly, it would help to disaggregate the data on educational attainment and productivity growth by demographic group. If we look at Canada, with it's massive surge of Asian immigrants, we see that these newcomers to Canada are not having the same dismal educational experience as America's Hispanic immigrants and Canada is managing to "get more" (36%+ of Chinese immigrants have some university, only 12% show no educational attainment) out of its new citizens than the US is managing with our new Hispanic residents. Even when we look beyond the immigrant generation and focus on their children, we see that Canada's policy of seeking to maximize human capital stocks when making immigration decisions results in these immigrants having children who exhibit better academic performance compared to our first generation Hispanic students despite the fact that Canada's public schools aren't financed as generously as ours (OECD Excel File) (Education Spending/Student 2000: Primary Level - Canada $6,120, US $7,980; Secondary Level - Canada = $5,947, US $8,855; Tertiary Level - Canada = $14,983, US = $20,358) and yet Canada isn't getting as "much out of" their citizens in terms of economic productivity as the US. So, whatever the US is doing right in terms of productivity growth it still manages to surpass most developed countries even when handicapped by unique demographic challenges. If Brooks would like to see educational attainment increase over time then he should really begin advocating that we stop importing poverty, stop fostering cultural diversity and begin trying to assess human capital stocks in our immigrants. Here's a hint for Brooks - you need to understand the parameters of a problem before you can hope to discuss it accurately - leaving out demographics when questioning national performance will forever lead you to misanalyze. Peoples and cultures matter. Don't take my word for it - here's what the official demographer of Texas has to say: Texas is changing. It is growing older and browner, with the elderly and Hispanic populations growing at an unprecedented rate. And as the populations increase, so will the challenges. Labels: Demographics
Monday, July 28, 2008
Tabarrok nails it.
Agnostic adds: Here's a graph using the new study's finding of same mean for males and females, and taking male to female ratio in variances to be 1.16 (they estimate it between 1.11 and 1.21). This is the ratio of a normal with mean = 0 and s.d. = 1.077 (male) to a standard normal (female). It's shown for above-average people, but it's symmetric about 0: males have more geniuses and more idiots. The dashed green line is M:F = 1, or perfect gender parity. Males are underrepresented between -1 and +1 s.d., and overrepresented outside this interval. You may have to click on the image to see it full-size. 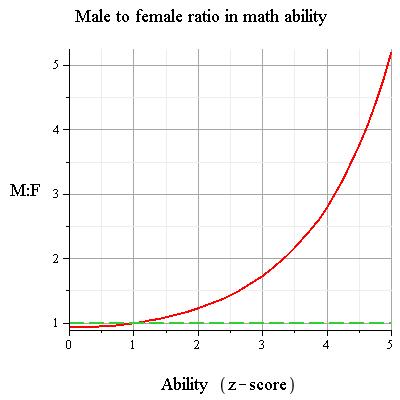 Labels: sex differences
Sunday, July 20, 2008
John Hawks is now a tenured professor at the University of Wisconsin, he's announced in the inaugural post of a four-part series on academic blogging. The entire thing is well worth a read for anyone who hopes to end up in a similar situation.
In my recent note on R. A. Fisher and epistasis, I mentioned that Fisher's theory of the evolution of dominance relied on the epistatic effect of 'modifier' genes. On looking again at the chapter in The Genetical Theory of Natural Selection dealing with the evolution of dominance, I see that there is a more general statement of the principle that the effect of a gene depends in part on the genetic background against which it occurs:
The fashion of speaking of a given factor, or gene substitution, as causing a given somatic change, which was prevalent among the earlier geneticists, has largely given way to a realization that the change, although genetically determined, may be influenced or governed either by the environment in which the substitution is examined, or by the other elements in the genetic composition. Cases were fairly early noticed in which a factor, B, produced an effect when a second factor, A, was represented by its recessive gene, but not when the dominant gene was present. Factor A was then said to be epistatic to factor B, or more recently B would be said to be a specific modifier of A. .... These are evidently only particular examples of the more general fact that the visible effect of a gene substitution depends both on the gene substitution itself and on the genetic complex, or organism, in which this gene substitution is made. Labels: Burbridge, Population genetics
Saturday, July 19, 2008
The recent report that the Duffy null allele is associated with increased risk of HIV infection recieved a lot of press (see Razib's comments on it here), mostly positive. In Nick Wade's New York Times article on the paper, however, some smart people publicly express some doubts. It's a tribute to Wade that he actually tries to summarize those doubts in the limited space allotted to him:
Dr. Goldstein said that in parts of the United States, African-Americans have a higher infection rate than European-Americans, and that patients with a higher proportion of African genes may be more vulnerable to H.I.V. for reasons unconnected to the SNP. Nonetheless, the SNP would show up in a greater proportion of infected people simply because of their African heritage. If so, the gene's apparent association with H.I.V. infection could be just coincidental, not causal.In somewhat more technical terms, the issue referred to here is the potential for false positives in an association study due to population structure[1]. The issues involved in accounting for structure in an admixture mapping study are somewhat more subtle than in a classic case-control study, but are generally similar. In particular, it's important to take individual levels of admixture into account[2]; this is generally done by including an estimate of individual admixture as a covariate in any regression model. The authors are aware of this potential confounder, and develop a measure of admixture based on 11 SNPs to include as a covariate in their regression. However, this measure is kind of weak, which I imagine in the sticking point for the skeptics in the Times article. If you have access to the supplemental information, take a look at it--several of these 11 SNPs are in the same gene, which means they're not independent, and several don't even have big frequency differences between African and European samples (if you're trying to judge via SNPs whether someone is more African or European, those SNPs better have a big frequency difference between Africa and Europe). This is probably not a precise measure of ancestry. In fact, the Duffy null allele they claim as associated is a better predictor of ancestry than any of these SNPs. So it's quite possible that the authors have simply shown a correlation between level of African ancestry and susceptibility to HIV (which could be due to any number of sociological, demographic, or genetic factors), rather than an association between Duffy null and susceptibility to HIV. Here's a relatively simple test of this possibility: genotype rs1426654 (the nonsynonymous SNP in SLC24A5) in their sample and perform exactly the same test as performed with Duffy. The motivation for this is that this SNP shares the property of Duffy null of being highly informative about ancestry, while being in a gene that presumably plays no role in HIV infection. If you get an association there, it seriously calls the Duffy result into question; if not, you feel a bit more comfortable. [1] For the classic extreme example of how population structure leads to false positive associations, consider a case-control association study on, say, diabetes, where the cases are all from Nigeria and the controls from France. Clearly, the cases are all going to have a high frequency of the Duffy null allele, and the controls are all going to have a low frequency (as Duffy null is essentially fixed in Africa and absent elsewhere), and one might naively conclude that Duffy null causes diabetes. But of course, the Duffy blood group has absolutely nothing to do diabetes (I don't think!), and the researchers have simply been confused by not matching their cases and controls. Obviously, this example is extreme, but more subtle population structure can also confound an association study (and methods for correcting for it are an active area of research; see here, for example) [2] It's well-known that African-Americans are an admixed population, with about 15-20% European ancestry on average. But there's great variability in this--a single sample of self-defined "African-Americans" can contain individuals with essentially no European ancestry and individuals who look genetically to be completely European. And on a larger scale, within the United States there's heterogeneity in admixture proportions as well (see Parra et al.). How could this create false positives? Essentially, if risk for a disease is correlated with ancestry for any reason, there's the potential for getting false positives. In this particular example, if HIV rates are higher in metropolitan areas where there's been more admixture, or if there are other genetic factors that make Europeans more resistant to HIV, etc., any "African allele" (like Duffy null) will show up as associated with HIV despite playing absolutely no role in the disease. Labels: Genetics
Friday, July 18, 2008
Gintis and Bowles have done great work cleaning up a lot of the discussion about cooperation, evolution, and economic outcomes. A Google Scholaring of their names turns up 14 items with over 100 citations, most of which would be well worth reading for GNXP regulars.
But that said, in their 2002 Journal of Economic Perspectives piece "The Inheritance of Inequality," they appear to make a small error. It's an error that's all-too-easy for even good folks to make: They apparently squared the h-squared. Their big insight and their small error are all part of answering a simple question: How much of the correlation of income between parent and child can be explained by the heritability of IQ? You might think it's straightforward: IQ is highly heritable, so if there's some channel linking IQ to income, then it's all over but the shouting. But numbers matter. And Gintis/Bowles work out the numbers, finding that there's a weak link in that causal chain: The low correlation (0.27 according to Gintis and Bowles) between IQ and wages. The causal chain goes like this: 1. Parental earnings have a 0.27 correlation with parent's IQ. 2. Heritability of IQ between parent and child is a bit more than 1/2 of h-squared (why a bit more? assortive mating). They take an h-squared of 0.5 for IQ. 3. Child's earnings have a 0.27 correlation with child's IQ. So the net result is 0.27*0.3*0.27 = 0.022 (page 10). A very small number, especially since the raw parent-child income correlation in U.S. data is about 0.4. So yes, knowing a parent's income helps you predict their adult (especially male) child's income. But only 5% (or 0.022/0.4) of the total correlation can be explained by IQ's impact on wages. Small potatoes. (Oh, but where's the small error? It's where Gintis and Bowles report that the net result is 0.01 instead of 0.022--a difference that I can most easily attribute to a mistaken squaring of the h-squared.) If I really wanted to get that net result up from a measly 5%--if I knew in my heart that IQ really was a driving force in intergenerational income inequality--then how would I do it? Well, I might use a higher heritability of IQ, I might assume more assortive mating, or I might assume a bigger correlation between wages and IQ. Hard to do much to budge that IQ/wage link: Zax and Rees's paper only has a 0.3 correlation between teenage IQ and middle-aged wages, and when Cawley, Heckman et al. regress NLSY wages on the first 10 principal components of the AFQT, they get a similar result. So you think maybe a higher heritability of IQ will save you? Well, let's just go all the way to perfect heritability of IQ and perfect assortive mating on IQ. In other words, let's see if "IQ clones" will be have enough similarity in wages to match the 0.4 intergenerational correlation of income. Will the IQ clones have similar incomes? Not so much. (0.3^2)*1 still equals something small: 0.09. Less than 1/4 of the intergeneration correlation in income. Medium-sized potatoes, but we had to make a ton of ridiculous assumptions to get there. It's that doggone low correlation between IQ and wages, a correlation that has to be squared because we're comparing parent to child. So a high heritability of IQ doesn't imply a high heritability of IQ-caused-income. Another reminder that lots of things impact your wages: Not just how smart you are. Gintis and Bowles work through some finger exercises to argue for big environmental effects, and that's all well and good. But to my mind, the interesting fact is that income is still highly heritable! G/B report that MZT (identical twin) earnings correlation is 0.56, and DZT (fraternal twin) earnings correlation is 0.36, so using the crudest of approximations, the heritability of earnings is still (0.56-0.36)*2=0.4. So income apparently has a modestly high heritability, but most of it can't be explained by the IQ-wage channel. Looks like the genetic heritability of income is being driven mostly by non-IQ channels. Labels: Behavior Genetics, Economics, IQ
Truism of the day: Introverted nerds don't get laid much. Or, in more scientific terms, extroversion in men is linked to a higher number of sex partners.[1] Men and women have similar levels of extroversion, though-- in fact, women have slightly higher levels of it.[2] This begs for explanation; after all, extroversion is significantly heritable (~50%)[3], so why shouldn't it have been positively selected for in males?
It turns out that, while men aren't more extroverted than women, they are more extroverted in the areas where it "counts.""The table below[2] of extroversion and its sub-traits sheds some light:
(mean difference is the mean difference between men and women on the trait. high %F and low %F are the percent of women who are at the very high and very low tail-ends of the distribution.) With the exception of 'ideas' (F-M=-1.6), a sub-trait of Openness to Experience, none of the 30 Big-Five sub-traits show more skew towards men than do assertiveness and excitement-seeking. While these -.9 and -1.5 mean differences may seem minor on their face, it is worth considering how they affect the tails of the distributions. In the case of sensation-seeking, 70% of people who are significantly low on excitement-seeking are female. A great deal of meaningful sexual dimorphism here, so let's look into it... Sensation-seeking Browsing through the sensation-seeking literature I came across this very interesting study; sensation-seeking was one of many variables examined in a study of college mens' number of sexual partners.[4] The other variables looked at (and all measured through questionnaires unless otherwise indicated) were: age, attractiveness (measured by self-rating, and female, male interviewer ratings), social intimacy, sexual affect, dominance, hypermasculinity, Eysenck's psychoticism trait measure, and testosterone levels (measured chemically through saliva samples). Sensation seeking correlated more so than any other variable with both lifetime number of sexual partners (.38) and with maximum partners in one month (.37). Trailing way behind it was hypermasculinity (.29, .29), followed by attractiveness (.20, .28).[4,5] I'm not going to attempt to unwind the complex causal chains which correlate sensation-seeking to short term mating success. It should suffice to say that there is significant evidence that these traits are both intrinsically attractive to women, and that they serve as an impetus to sexual pursuit of women by men in the first place.[7] Sensation- seeking has the highest narrow-sense heritability of any (Big-5) sub-trait-- .36, and a relatively high broad-sense heritability of .52, by the way.[3] A Pet Hypothesis It seems plausible that sensation-seeking garnered a greater number of female mates in the Pleistocene , just as it does now, and that there was therefore positive selection for it in men. I would posit that if this positive selection existed, it was limited in effect by the negative aspects of extroversion, visible in our day in age-- extroverts are more at risk for STD's, being jailed, getting in fights, and generally doing stupid risky things. The fact that Extraversion has a higher degree of heritability in men than in women (.57 versus .38)[3] might be considered as evidence. I am not knowledgeable enough of the behavior genetics involved to say whether this is meaningful evidence. The most specific, and testable part of my hypothesis is this: that ADHD (note that I'm not saying ADD) is to some extent the result of "overclocking" for male sensation-seeking. Consider this-- estimates of the male:female ratio for ADHD range from 4:1 to 9:1.[8] People with ADHD are more extroverted than other people, yes, but they are especially more sensation-seeking than other people. Unsurprisingly, people with ADHD have a higher number of sexual partners than people without.[9] The discrepancy between males without ADHD and those with it is probably underestimated because of the widespread use of drugs like Ritalin. Notes 1. (Nettle 2004). 2. (Corbitt & Widiger 1995). See the table in their article for all of mean differences and percentile differences at the tails of the bell curves between men and women. 3. (Loehlin & Bouchard, 2001) 4. (Bogaert et. al 1995) 5. Sensation seeking correlated trivially with age, .14 with Attractiveness, .26 with dominance, .41 with hypermasculinity, and .45 with psychoticism. Statistically eliminating virgins from the sample had no major effects on these correlations. For you data crunchers out there I suggest you read the study yourself if you want to analyze their factor and regression analyses. 6. (McCoul & Haslam 2001). 7. There's a good summary of some of the studies on why sensation-seeking might cause more mates in (McCoul & Haslam 2001). 8. (Gutman 2002) 9. (White 1998) References
Labels: Personality, sex, sex differences
My next note on Sewall Wright will cover the exciting subject of the adaptive landscape. As every schoolboy knows, Wright considered epistatic gene interactions very important in determining the 'peaks' of the landscape. A sharp contrast is sometimes drawn between Wright and R. A. Fisher in this respect. For example:
What is said here about Wright seems broadly correct, but what is said about Fisher is seriously misleading. Before continuing with my notes on Wright, I will therefore try to clarify Fisher's views on epistasis.[Note: due to formatting problems, italics and other refinements may be omitted.] First, it is necessary to say something about the meaning of epistasis. The term 'epistasis' itself seems to have emerged around 1917. The first use cited in the OED is from the index to the 1917 volume of the journal Genetics. Around the same time Fisher, in writing his 1918 paper on the Correlation of Relatives, coined the term 'epistacy', but this never caught on. Both terms were derived from the adjective 'epistatic'. Like much of the terminology of genetics (including the word 'genetics' itself) this was coined by William Bateson, in 1907. Bateson used it with a relatively limited meaning to describe cases where a gene at one locus masked or suppressed the action of genes at another locus. For example, genes at one locus might affect the pigmentation of an animal's fur, but a gene at another locus might suppress the production of pigment entirely, causing albinism. In this case the trait of albinism (or the gene producing it) would be called epistatic (literally 'standing over'), while the traits that were masked would be called 'hypostatic' (literally 'standing under'). This limited usage of 'epistatic' is still sometimes found in medical genetics, but in evolutionary genetics a wider usage is more common. In the wider usage, epistasis is any kind of interaction between genes at different loci. Of course, many traits are affected by genes at more than one locus, but this does not necessarily imply interaction. The meaning of 'interaction' is that the genes at different loci do not act independently. For qualitative traits, the usual test of this is that the traits of the offspring do not show the expected Mendelian ratios (which is how epistasis in Bateson's sense was originally discovered). For quantitative traits, the usual criterion is that the value of the trait is not simply the sum of the values attributable to the individual genes concerned. If it is simply the sum, the genes are often said to have a purely 'additive' effect. If not, the trait either shows dominance (if the interaction is between genes at the same locus) or epistasis (if at different loci). Assuming that epistasis can be identified (which in practice is often very difficult for small effects), it may be asked how the effects of epistatic interaction on a quantitative trait can be measured. One answer to this would be to decide that where interaction is involved, the entire effect of the interacting genes should be counted as epistatic. But this seems unreasonable if the same genes would still have some effect even if there were no interaction. An ideal solution might be to find cases in which the genes concerned are not involved in any epistatic relations, and measure their effect in these circumstances, then subtract this from the effect in the case of epistasis. But if epistasis is a widespread phenomenon, it would be difficult to find these non-epistatic cases, since most genes would show some effects of interaction. In any event, a different approach is generally taken. The usual approach to measuring the effects of epistasis is roughly as follows. Each gene is assigned a value (the 'average effect' of the gene) based on the average value for the trait concerned among those members of the population who carry that gene, expressed as a deviation from the population mean. Each genotype (gene combination) is then assigned a value based simply on the sum of these average values. This is called the 'breeding value', since it is the part of the genetic makeup of the individual which enables the traits of its offspring to be predicted for breeding purposes. These breeding values will have a certain variance, relative to the population mean, usually called the additive genetic variance. The actual observed values will have a greater variance than this, due to the effects of environment, dominance, epistasis, and various other complications. The portion of the observed variance attributable to epistasis is estimated after the effects of environment and dominance have been subtracted. Genes with epistatic effects are not excluded from the analysis, and they may contribute to both additive and (in a more complicated way) to dominance variance as well as to the specific epistatic or 'genetic interaction' variance. All this is explained more fully, and no doubt more clearly, in Falconer. For a simple worked example of my own see Note 1. The standard terminology is unfortunate. It cannot be stressed too strongly that 'additive' variance is not the same as the variance due to genes with purely additive effects. The additive variance takes account of the average effects of all genes, including those that may show strong dominance or epistasis. These average effects depend in part on the gene frequencies present in the population in question, and assume that all possible genotypes occur in the proportions expected under a given system of mating (usually assumed to be random). Part of the average effect is therefore due to the effects of gene interactions. Conversely, the so-called 'epistatic variance' covers only a part - usually the minority - of the effects that might intuitively be ascribed to interaction. Enthusiasts for epistasis (as in the volume already cited) sometimes complain that the standard method of apportioning variance tends to understate the effects of epistasis, and makes it difficult to detect. For example, James Cheverud comments that 'most tests for epistasis rely on the epistatic variance alone and ignore its contribution to additive and dominance variance' (p.65) and Edmund Brodie says that 'under a wide range of allele frequencies and strengths of interaction, the majority of variance produced by gene interaction is actually additive' (p.10). It would be possible in principle to use alternative measures which assign more of the observed variance to epistasis. But the standard method does have the advantage that it is possible to estimate the additive variance from the observed correlation between parents and offspring, and conversely to estimate the value of offspring from that of parents. This is particularly important if we wish to predict the effects of natural or artificial selection. Whatever we call it, the 'additive' variance is a useful concept and is not going to go away. It is also desirable to distinguish between epistasis for fitness and for other traits of the organism. Fitness itself (whether measured simply by number of offspring or otherwise) shows epistasis if the effects on fitness of genes at different loci are not purely additive. If fitness is measured in relation to some particular trait, the fitness may show epistasis even if the trait as such does not. (And presumably vice versa, though I cannot think of a plausible scenario for this.) For example, a trait such as body size might be influenced by several genes acting purely additively in their effects on body size, but epistatically in their effect on fitness. This will often be the case if fitness is highest for some intermediate value of the trait. The fitness effects of genes tending to raise (or lower) the value of the trait will then depend crucially on the other genes they happen to be combined with. In the simplest case, if there are two haploid loci, with alleles H and L (for High and Low) at one locus, and h and l at the other, the combinations Hl and hL, which give intermediate size, may be favoured by selection, while the combinations Hh and Ll, which give high and low size respectively, are selected against. In this case the fitness is epistatic even though the direct effect of the genes on the phenotype is additive. After all these preliminaries, I turn to discuss what Fisher actually said about epistasis. Correlation of relatives As already mentioned, Fisher's great 1918 paper on the 'Correlation of Relatives' proposed the term 'epistacy' to allow for the interaction of genes at different loci, and devised the standard method for apportioning variance. Fisher introduces his definition of 'epistacy' as follows: 'There is in dominance a certain latency. We may say that the somatic [phenotypic] effects of identical genetic changes are not additive, and for this reason the genetic similarity of relations is partly obscured in the statistical aggregate [see Note 2]. A similar deviation from the addition of superimposed effects may occur between different Mendelian factors [genes at different loci]. We may use the term Epistacy to describe such deviation, which although potentially more complicated, has similar statistical effects to dominance. If the two sexes are considered as Mendelian alternatives, the fact that other Mendelian factors affect them to different extents may be regarded as an example of epistacy. The contributions of imperfectly additive genetic factors divide themselves for statistical purposes into two parts: an additive part which reflects the genetic nature without distortion, and gives rise to the correlations which one obtains, and a residue which acts in much the same way as an arbitrary error introduced into the measurements. ' (p.404) Note that Fisher says here quite explicitly that part of the contribution of 'imperfectly additive' genes is itself additive, or as we would say, falls within the additive variance. Fisher does not say a great deal more about 'epistacy' in this paper (but see p.408-9 for the mathematical treatment of epistatic variance), and one of the contributors to the volume cited earlier claims that in his 1918 paper Fisher 'dismissed gene interactions as being of only minor importance in the evolutionary process, analogous to nonheritable modifications of the phenotype' (p.125). This goes beyond anything Fisher says. What he does say is that 'Throughout this work it has been necessary not to introduce any avoidable complications, and for this reason the possibilities of Epistacy have only been touched upon...' (p.432). For Fisher's specific purpose in this paper, which was to explain the correlation between relatives on Mendelian principles, and not to discuss evolutionary theory in general, his brief treatment of 'epistacy' seems sufficient. Fisher finds that with his methods the existing data on the correlation of relatives (mainly the data of Karl Pearson on humans) can be explained satisfactorily by additive variance, dominance, and assortative mating, without much influence of other factors, which by implication include epistatic variance. Fisher is more explicit about this in his 1922 paper on the Dominance Ratio, where he says that 'special causes, such as epistacy, may produce departures [from the expected correlations], which may in general be expected to be very small from the general simplicity of the results'. But before interpreting this as a general pronouncement on the insignificant role of epistasis in evolution, we should note that (a) the additive variance includes much of the effect of 'epistatic' genes, and (b), the discussion was concerned with ordinary traits such as height, and not with fitness. As emphasised earlier, there may be epistasis for fitness even if the underlying traits are purely additive. The evolution of dominance One of Fisher's best-known, and most controversial, theories is that of the evolution of dominance. Noting that harmful mutations are usually (though not always), recessive in their effects, Fisher sought to explain this by the action of modifier genes at other loci, which would be gradually selected to minimise the harmful effects of common recurring mutations by making them recessive. The theory has not been generally accepted, and Wright in particular opposed it, mainly on the grounds that the selective advantage of modifier genes would be so weak that it would usually be overpowered by their other, more direct, effects. Regardless of whether Fisher was right or wrong on this issue, the point to note here is that his theory depends entirely on epistatic effects! In this respect, at least, Fisher was more enthusiastic about epistasis than Wright himself. Mimicry A whole chapter of the Genetical Theory of Natural Selection is concerned with Mimicry. In discussing the underlying genetics of mimicry, Fisher emphasises the role of modifier genes, including those that act as 'switches' for other genes. For example, discussing the 'hooded' gene in rats, he says 'The gene, then, may be taken to be uninfluenced by selection, but its external effect may be influenced, apparently to any extent, by means of the selection of modifying factors' (p.185). And in discussing another case he goes on to say 'The gradual evolution of such mimetic resemblances is just what we should expect if the modifying factors, which always seem to be available in abundance, were subjected to the selection of birds or other predators' (p.185). While modifiers might in principle be purely additive in effect, they are more likely to be epistatic. This is presumably always the case with 'switch' genes. Sex Chapter 6 of GTNS deals with a variety of issues concerning sex, sexual selection, sex-limited traits, and speciation. Some of these could well involve epistasis - indeed, 'sex-limited' traits (those which are only manifested in one sex) do so almost by definition, if sex is genetically determined. (As mentioned in Fisher's paper on 'Correlation of Relatives', quoted above, differences between the sexes can be regarded as a case of 'epistacy'.) However, I find only one definite reference in the chapter to epistatic effects. In his discussion of speciation, Fisher points out that the adaptiveness of genes will vary in the different parts of a species's range, and says that 'In addition to those genes which are selected differentially by the contrasted environments, we must moreover add those, the selective advantage or disadvantage of which is conditioned by the genotype in which they occur, and which will therefore possess differential survival value, owing not directly to the contrast in environments, but indirectly to the genotypic contrast which these environments induce' (p.141). A difference in the selective advantage of a gene according to the genotypic background implies epistatic fitness. What Fisher is describing here is actually what is often called a 'co-adapted gene complex', much beloved of Wrightians. The Fundamental Theorem of Natural Selection The Fundamental Theorem of Natural Selection states that 'The rate of increase in fitness of any organism at any time is equal to its genetic variance in fitness at that time' (GTNS p.37). The FTNS is notoriously difficult to interpret, and I do not intend to say much about it here. It is however now generally accepted, following the interpretations by George Price and A. W. F. Edwards, that when Fisher refers to 'genetic variance' he means the 'additive' genetic variance. The additive variance takes account of the average effect of genes in all the various environmental circumstances and genetic combinations in which they are found, in the proportions to be expected under a given system of mating. (See expecially p.31 of GTNS, where Fisher defines 'average excess' and 'average effect'.) It therefore incorporates the effects of dominance and epistasis to the extent that these contribute to the additive value of the genes. There is no reason at all to suppose that genes with epistatic effects are excluded from the FTNS. What is excluded is only that part of the total variance that is not covered by the contribution of those genes to additive variance. This can be justified on the grounds that the non-additive variance does not predictably change gene frequencies in the next generation and therefore has little effect on evolution. As Cheverud admits, 'the rate of evolution is determined by the additive genic [sic] variance alone' (p.65). Selection at two loci Before 1930 neither Fisher nor Wright had treated selection at more than one locus. As so often, the pioneer of the subject was J. B. S. Haldane, in 1926. In 1930 Fisher did however give the subject a short section in Chapter 5 of GTNS, under the heading 'Equilibrium involving two factors'. (This chapter is one of several that appear to be invisible to some readers.) The interesting situation, as Fisher recognises, is where two different combinations of alleles (e.g. AB and ab) are both favoured by selection, while the same genes are disadvantageous in other possible combinations (e.g. Ab and aB). Fitness in this case is therefore clearly epistatic. In his chapter summary Fisher says that stable equilibria may be established, but he is rather vague about the conditions for stability. But his main point is that there will be selection in favour of closer linkage between favourable gene combinations on the same chromosomes, and it is therefore a puzzle why recombination is as frequent as it is. I think this remains a problem. In any event, it is a case where Fisher clearly recognised the role of epistasis. Selection of metrical characters One of the most intriguing, but difficult, sections of GTNS is the one (also in the 'invisible' Chapter 5) on 'Simple metrical characters'. (I sometimes wonder if Fisher's use of the word 'simple' was a sly joke.) The case of interest is where a quantitative character, such as the size of a tooth, is regulated by genes at more than one locus, and subject to stabilising selection in favour of an intermediate size. Egbert Leigh has described this (in his 'Afterword' to the 1990 reprint of Haldane's 'The Causes of Evolution') as 'a topic still replete with mysteries and surprises'. Fisher's account is even more tangled than most, because he attempts to explain simultaneously selection of the metrical trait itself and selection for dominance of the genes controlling it. I cannot pretend to understand everything he says on the subject, but what is clear for the present purpose is that fitness in this case is epistatic, and that there may be more than one outcome of selection, depending on the initial frequencies of the genes concerned: 'the conditions of equilibrium are always unstable. Whichever gene is at less than its equilibrium frequency will tend to be further diminished by selection' (p.121). This is precisely the situation which Wright often emphasised as leading to alternative 'selective peaks'. But unlike Wright, Fisher did not believe a species was likely to get 'stuck' permanently on a selective peak (not that Fisher had much time for the adaptive landscape anyway). Fisher believed that following any change in the optimum phenotypic value due to environmental change there would be sufficient genetic variation (in a large population) for selection to shift organisms quickly towards the new optimum. His confidence in this was based mainly on the results of artificial selection, as he referred to 'the extreme rapidity with which such measurements are modified when selection is directed to this end' (p.119). The effects of such changes on gene frequencies might be lasting, even if the initiating circumstances were temporary. In Fisher's analogy, which may be more illuminating to physicists than to me, 'the system resembles one in which a tensile force is capable of producing both elastic and permanent strain, and in which the permanent deformations always tend to relieve the elastic forces which are set up' (p. 125). This section of GTNS raises a rather intriguing historical possibility. As Provine has noted in his biography of Wright (Provine p.285-6), there was an unexplained change in Wright's account of the 'shifting balance' theory between his exposition in 'Evolution in Mendelian Populations' (1931), and his next major account in 1932. In 1931 he had asserted that temporary changes in the environment would only have temporary effects on the gene pool, being essentially reversible. Hence his emphasis on genetic drift in small subpopulations, as the only possible means of shifting from one peak to another. In 1932, on the other hand, he accepted that environmental changes could also shift a population from one stable peak to another, so that their effects might be lasting even after the change in environment had reversed. Unfortunately Wright did not explain the reasons for his change of mind, nor did he draw attention to the change, which is really very important, since it greatly weakens Wright's argument for the importance of genetic drift in small local subpopulations. Provine speculates, plausibly enough, that Wright's correspondence with Fisher, his reading of GTNS, and Fisher's own published review of 'Evolution in Mendelian Populations', had something to do with the change. My own suggestion, to build on this, is that Fisher's discussion of metrical characters in Chapter 5 of GTNS was a particular influence. But I have no direct evidence of this, so it will probably remain a mere speculation. Conclusions The main purpose of this note has been to identify and document what R. A. Fisher himself, as opposed to the straw man 'Fisher', actually said and believed about epistasis. Readers will be able to draw their own conclusions, but I will briefly indicate my own. a) Fisher did not deny the existence of epistasis, in the broad sense, and in some specific cases - including the evolution of dominance, selection at two loci, and quantitative (metrical) traits under stabilising selection - he gave it an important role. b) Fisher agreed with Wright (and Haldane) that in some circumstances, including stabilising selection, there could be more than one outcome of selection in terms of the resulting gene frequencies. Unlike Wright (in 1931), but like Wright (in 1932), he believed that temporary environmental change could shift a population durably from one equilibrium set of gene frequencies to another. Fisher's treatment of the problem in GTNS may have influenced Wright's unexplained volte-face on this important issue. c) Fisher did not believe populations were likely to get stuck on a local peak in the selective landscape, but this was not because he did not believe in epistatic effects, but because he did not believe in the validity of the selective landscape concept at all. I will probably say more about Fisher's thinking on this in another post. d) Fisher's general concept of evolutionary change, as expressed in the Fundamental Theorem of Natural Selection, does not exclude epistatic effects. The FTNS takes account of epistasis (and dominance) precisely to the extent that they do affect the rate of evolutionary change. The FTNS is neutral with respect to the importance of epistasis: whether it is important or unimportant cannot be inferred from the theorem, which takes account of additive variance in fitness whatever its source. Unfortunately much confusion has arisen about the meaning of 'additive' and 'epistatic' variance. If it is not understood that 'additive' variance includes much of the effect of epistatic genes, while 'epistatic' variance excludes much of that effect, the scope of the FTNS will be seriously misconstrued. It would be better to call additive variance something like 'heritable variance', while the non-additive effects of dominance and epistasis are clearly labelled in such a way as to make it clear that they are only part of the total effect of gene interactions. e) Unlike Wright, Fisher did not, at least in his published works, put any emphasis on epistasis as a major factor in evolution. It is necessary to read GTNS quite carefully (or at least to look at all the chapters!) to find the references I have gathered together here. It is an empirical matter whether epistasis plays the central role that Wright gave it. Or it might have an important role that neither Wright nor Fisher had thought of, as suggested in Kondrashov's theory of sex. I have not dealt here with another aspect of Fisher's views, namely his rejection of the importance in evolution of large single mutations. I have no doubt that Fisher believed that evolution occurred mainly through the selection of a large number of genes with individually small effects. I have not discussed this because (a) it was not a point of disagreement between Fisher and Wright, and (b) it does not seem relevant to the issue of epistasis. As far as I can see, large mutations are no more or less likely to have epistatic effects than small ones. Addendum After writing the above, I came across a further reference to epistasis in Fisher's correspondence. Writing to Leonard Darwin in 1928, Fisher said 'I am inclining to the idea that the main work of evolution lies in the discovery by trial of perhaps rare combinations of its existing variants, which work better than the commoner combinations. A slight increase in the number of individuals bearing such a favourable combination will then set up selection in favour of all the genes in the combination, with marked evolutionary results. Many of these genes would have been previously rare mutant types (not necessarily rare mutations) unfavourable to survival. I think of the species not as dragged along laboriously by selection like a barge in treacle, but as responding extremely sensitively whenever a perceptible selective difference is established. All simple characters, like body size, must be always very near the optimum, so much so that the average body sizes of two alternative genes must be balanced on either side of the optimum, selection always tending to eliminate the rarer because it is further from the optimum...' (Correspondence p.88). In his Introduction to the correspondence, J. H. Bennett draws attention to this letter, and remarks that 'It is interesting, and perhaps needs emphasizing, that both Fisher and Wright considered systems of interacting genes to be of critical importance in evolution. A fundamental difference in their views of the evolutionary process concerned the means by which interaction systems could be exploited' (p.47) While I agree with Bennett that Fisher took some account of 'interaction systems' , in other words epistasis in the broad sense, this letter of 1928 seems a good deal more positive on the subject than anything I have noticed in his published works. I take this opportunity to say that Bennett's Introduction is one of the most useful things yet written on Fisher's work and ideas, and deserves repeated reading. Note 1 Consider the simplest case of a haploid organism with a quantitative trait determined by genes at two loci. I assume complete genetic determination. Let the alleles in the population be A and a at one locus, and B and b at the other, each with a frequency of 50% in the population. Under random mating the four genotypes AB, Ab, aB and ab will therefore all have the frequency 25%. (In a diploid there would be nine genotypes to consider, and the possible complication of dominance, which is why I have chosen the haploid case.) Let us suppose that the measurements of the trait for the four genotypes are as follows, where c and d are any numerical values: AB........c + d Ab........c aB........c ab.........c I have chosen these values to dramatise the situation. Intuitively, one would say that all of the variation in the trait was due to the epistatic interaction of A and B, since all other genotypes than AB have the identical value c. So let us see how the variance comes out under the standard method. The mean value of the trait in the population is evidently .75c + .25(c + d) = c + .25d. The mean values for each gene considered separately, measured by the average value of the individuals who possess that gene, are: A........ .5(c + d) + .5c = c + .5d a......... c B........ .5(c + d) + .5c = c + .5d b........ c Expressed as deviations from the population mean, c + .25d, these values come out as: A........ + .25d a......... - .25d B........ + .25d b........ - .25d These are known as the 'average effects' of the genes in question. The so-called 'breeding value' of a genotype is simply the sum of the average effects of its component genes, so for the four genotypes we have the breeding values: AB.......... + .5d Ab.......... 0 aB.......... 0 ab.......... - .5d It may be noted that the combination ab has a substantial (negative) breeding value, even though there is, intuitively, no interaction between a and b. This reflects the fact that the interaction of A and B pulls up the population mean, and therefore affects the deviation values of other alleles and genotypes. The combination ab falls as far below the resulting mean as the combination AB rises above it. The symmetry is of course a consequence of the symmetry of the chosen assumptions about gene frequencies, etc. The breeding values are already deviations from the population mean, so for the variance of breeding values (the so-called additive genetic variance) we have: .25(.5d)^2 + .25(0)^2 + .25(0)^2 + .25(.5d)^2 = .125d^2. It is already apparent that although the variance is intuitively entirely due to epistasis, the 'additive' variance is not zero. For comparison, we can measure the total variance of the values of the genotypes. The deviation values are as follows: AB.......... c + d - (c + .25d) = .75d Ab, aB, and ab.......... c - (c + .25d) = - .25d Taking account of the proportions of the genotypes in the population we therefore have the variance of genotypic values as follows: .25(.75d)^2 + .75(- .25d)^2 = .1875d^2 Subtracting the 'additive' variance from the total genotypic variance we find only .0625d^2 left for the 'epistatic' variance. So even where we have rigged the example to give a strong influence to epistasis, 2/3 of the resulting variance is 'additive', and only 1/3 'epistatic'! Note 2: I think that by 'genetic changes' in this sentence Fisher means not just mutations, but any gene substitution, such as may occur through the normal processes of sexual reproduction. So, for example, if at a single locus the combination aa is replaced by the combination Aa, there will be a certain measurable effect of the change. If the effect of substituting two As is twice the effect of substituting just one A, the effect is additive. Otherwise the locus shows some degree of dominance. References: D. S. Falconer: Introduction to Quantitative Genetics, 3rd. edn., 1989 R. A Fisher: The Genetical Theory of Natural Selection, 1930. I have given page references to the revised Dover edition of 1958, but the quoted passages are all unchanged from the first edition. For scholarly purposes the best edition is now the Variorum edition of 1999, edited by Henry Bennett. Fisher's papers are cited from the online copies available from the archives at Adelaide (see link on sidebar) Natural Selection, Heredity and Eugenics: Including selected correspondence of R. A. Fisher with Leonard Darwin and others, edited by J. H. Bennett (1983). Much of the correspondence is also available online from the archives at Adelaide. Epistasis and the Evolutionary Process, ed. J. B. Wolf, E. D. Brodie, and M. J. Wade. 2000 William B. Provine: Sewall Wright and Evolutionary Biology, 1986. (Paperback edn. 1989) Labels: Burbridge, Population genetics
Thursday, July 17, 2008
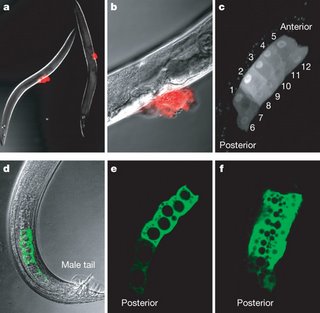 Model organisms are models for a number of reasons: they're relatively easy to work with in the lab, or there are a lot of experimental tools available, or maybe even simple interia. But given that they're models and various neat mutagenesis assays are available for toying around with them, people often forget that even model organisms often show a massive amount of natural variation. There's a reason to map this natural variation over variation due to mutagenesis: it's been visible to selection, and so may highlight key nodes of networks that are open for adaptive (or neutral change). Model organisms are models for a number of reasons: they're relatively easy to work with in the lab, or there are a lot of experimental tools available, or maybe even simple interia. But given that they're models and various neat mutagenesis assays are available for toying around with them, people often forget that even model organisms often show a massive amount of natural variation. There's a reason to map this natural variation over variation due to mutagenesis: it's been visible to selection, and so may highlight key nodes of networks that are open for adaptive (or neutral change). A beautiful example of this has just been published in an elegant paper in Nature, in the nemotode C. elegans. In some strains of this species, after a male mates with a hemaphrodite (males are rare, and most reproduction occurs via selfing), it deposits a "copulatory plug" that decreases the fitness of those males that follow him (stained red in the figure on the right). In other strains, there's no such plug. So a natural question is: what's the genetic basis for this phenotype, and what is its evolutionary history? First, the answer to the first question: the authors map the trait to a retrotransposon insertion into a previously unknown gene. This gene share homology with the mucins, and is specifically expressed in around 12 cells of the male vas deferens (in green on the right). Personally, I never cease to be amazed by the discovery of new genes in sequenced model organisms, but it's happened so much that perhaps I should get used to it. The authors then go on to show that strains that express the plug overlap in their ranges considerably with strains that don't. This suggests little fitness effect of the retrotransposon insertion, and this seems to make sense--C. elegans evolved from a species with obligate male=female reproduction (where presumably the plug was advantageous) to a species where most reproduction is by selfing (where a plug is likely more neutral). Overall, a really nice story. Labels: Genetics
Wednesday, July 16, 2008
Sebastian Flyte has a critique of my overuse of Latin. One thing I do want to add is that it's not all part of my "style," I used to the term "thickly scaffolded" in the post Sebastian highlights to allude to thick description, which I assume some of you will know about. I guess I could have referred explicitly to thick description, but I thought the idea of a scaffold was more precise in terms of what I perceived the exposition style of Ross & Reihan in GNP to be (and since many here have molecular biology in the background I also thought it would be a useful word to put there). But yeah, I use a lot of Latin-derived terms....
Tuesday, July 15, 2008
Genetic Diversity and Economic Development: A Goldilocks Story
posted by
Herrick @ 7/15/2008 11:22:00 PM
From Oded Galor and his promising grad student Quamrul Ashraf, another paper that ties together genes and group productivity.
Their big result (Figure 5 below) is that a population cluster's genetic heterozygosity has a Goldilocks relationship with population density in 1500AD: Too much heterozygosity (Sub-Saharan Africa) or too little heterozygosity (Americas) predicts low population density. And in a pre-modern world (heck, even in the modern world), population density is a rough measure of technological progress. 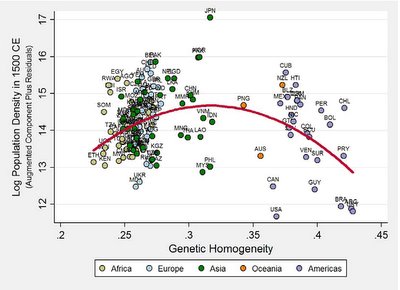 Surprisingly, the Goldilocks result holds even when you control for a bunch of other stuff like arable land and the timing of a population's agricultural transition. And perhaps most surprisingly, the much-hyped correlation between latitude and population density vanishes when you control for pretty much anything in addition to latitude. So the "distance from the equator" variable that growth economists spend so much time on may just be epiphenomenal. The authors admit they don't have a great theory for why the warm porridge tastes best–the goal of their paper is basically to get the Goldilocks result out there for others to work on. Here's hoping some economists take the bait..... Bonus: Portfolio's Zubin Jelveh gets Galor to comment on what all this means for Jared Diamond.  In the post below, Colder climates favor civilization even among Whites alone, I made a few comments about possible differences between Germans in Illinois and Germans in Texas, based on nothing much more than a hunch. I trust my hunches, but there's no reason you should, so I decided to see if there was anything here in regards to my assumption about interregional differences in intelligence and how they might track across ethnic groups. So of course I went to the GSS website, and checked the mean WORDSUM scores of various white ethnic groups broken down by region. I specifically focused on whites who stated that their ancestors were from England & Wales, Germany and Ireland. My reasoning is that these are three groups with very large N's within the GSS sample and they are well represented across the regions in absolute numbers. My main motivation was see if the differences across regions were similar for all three groups. Here are the states for each region (the Census made up these categories): In the post below, Colder climates favor civilization even among Whites alone, I made a few comments about possible differences between Germans in Illinois and Germans in Texas, based on nothing much more than a hunch. I trust my hunches, but there's no reason you should, so I decided to see if there was anything here in regards to my assumption about interregional differences in intelligence and how they might track across ethnic groups. So of course I went to the GSS website, and checked the mean WORDSUM scores of various white ethnic groups broken down by region. I specifically focused on whites who stated that their ancestors were from England & Wales, Germany and Ireland. My reasoning is that these are three groups with very large N's within the GSS sample and they are well represented across the regions in absolute numbers. My main motivation was see if the differences across regions were similar for all three groups. Here are the states for each region (the Census made up these categories):New England - Maine, New Hampshire, Vermont, Massachusetts, Rhode Island, Connecticut Middle Atlantic - New York, New Jersey, Pennsylvania East North Central - Ohio, Indiana, Illinois, Michigan, Wisconsin West North Central - Minnesota, Iowa, Missouri, North Dakota, South Dakota, Nebraska, Kansas South Atlantic - Delaware, Maryland, District of Columbia, Virginia, West Virginia, North Carolina, South Carolina, Georgia, Florida East South Central - Kentucky, Tennessee, Alabama, Mississippi West South Central - Arkansas, Louisiana, Oklahoma, Texas Mountain - Montana, Idaho, Wyoming, Colorado, New Mexico, Arizona, Utah, Nevada Pacific - Washington, Imbler, California, Alaska, Hawaii Obviously the breakdown isn't ideal. I think Delaware and Maryland arguably should be Mid-Atlantic. I also believe that Wisconsin is more plausibly in the West North Central than Missouri or Kansas is. But those are the regional breakdowns and I can't do anything about them. So, WORDSUM is a vocabulary test on a 0-10 scale. For the whole GSS sample the mean was 6.00, with 1 standard deviation being 2.16. Below is a chart which shows the relationship between WORDSUM scores (Y axis) for various regions (X axis) for each of the three ethnic groups: 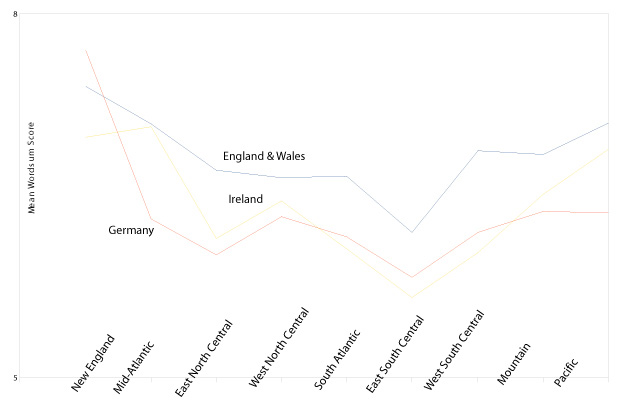 The tables below are pretty self-explanatory. At the top you see the mean WORDSUM scores for each ethnic group for each region. I put the N's in there as well so you can see that the sample sizes were pretty big. Note that there is more interregional variation within an ethnic group than there is interethnic variation within a region (the standard deviation across the columns is 50% bigger than across the rows). Just to be clear, I also included some tables which show the differences in WORDSUM mean scores between the regions like so: (row - column) = value.
Labels: civilization, climate, crime, education, GSS, IQ, true redneck stereotypes
Colder climates favor civilization even among Whites alone
posted by
agnostic @ 7/15/2008 02:12:00 AM
Last year I had a crazy idea about how winged insects might influence civilization. I only pointed to winged insects as an exemplar, not to suggest a "Mosquito Theory of History" or something stupid and sexy like that. The reasoning is simple: insects are more likely to be winged in certain climates, and that means more effective vectors of disease in such environments; and a greater disease burden makes you dumber, more tired, and more irritable, which stunts the growth of civilization. [1] A qualitative follow-up post looked at where civilizations have ever appeared, and in what climate types they existed.
Well, now I've done some quantitative work, and it turns out that I was right. One critique against an international study is that natural selection may have adapted people to be more or less civilized in different environments, so that the only influence of climate is as a selection pressure for genetic change. There are at least two such studies already out there: one by Templer & Arikawa (2006) and another by Vanhanen (2004). I'm arguing that it matters even when people start out pretty much the same genetically, so I will look just at the US. It varies enough in climate and degree of civilization that any correlation should jump out. Motivation In particular, I will look at the correlation, on the level of states, between average annual temperature and the average IQ of Whites, post-secondary degrees awarded to Whites per capita, and the percent of the White population that's imprisoned. I only look at Whites in order to avoid the confound of climate with racial composition (for example, the cold Mountain states are heavily White, while Blacks make up a larger fraction in the hot Southeast). The reason I look at basic measures like IQ or being in jail, as opposed to the loftier things we associate with civilization, is that smarts is the key determinant of propelling the institutions of civilization forward, while crime gives us a good rough idea of how barbaric we are on a personal level. I'm sure that governments can improve or screw things up too, but it's the raw cognitive and behavioral materials that matter most, as Lynn and Varhanen show in IQ and the Wealth of Nations (see all GNXP posts on this topic). Moreover, studies of representative samples of the population always show a strong influence of IQ on how cultured a person is. See, for example, a National Endowment for the Arts report on the demographics of arts attendees (PDF p. 19), which shows that attendance increases nearly monotonically by education level. The results As you can see, hotter average temperature is associated with lower White IQs, fewer degrees being awarded to Whites per capita, and a higher percentage of the White population being imprisoned. The relationship looks pretty linear in each case, and the data are on an interval scale, so we check the Pearson correlation coefficient: between White IQ and temperature, it is -0.48 (p = 0.0005, two-tailed); between degrees to Whites and temperature, it is -0.57 (p = 0.00002, two-tailed); and between percent of Whites in jail and temperature, it is +.40 (p = 0.005, two-tailed). Even conservatively correcting for three independent hypotheses still leaves all results significant (and IQ and getting a college degree are not even independent). At any rate, average temperature accounts for 23%, 32%, and 16% of the variance in White IQ, degrees to Whites, and percent of Whites in jail, respectively -- pretty damn good for social science. [2] Methods I took the average annual temperature for each of the 48 continental states (Alaska and Hawaii were not included in the source, so I left them out). Next, I used Audacious Epigone's estimates of White IQ by state, which are based on NAEP data from 8th grade math and science test scores (read about his methods here). I turned to Statemaster.com for the per capita number of post-secondary degrees awarded to Whites. For the number of Whites in prison per 100K Whites in the state's population, I used the data from 1997 in a study by the National Center on Institutions and Alternatives (PDF here), which separates non-Hispanic Whites from Hispanics, unlike most crime data from government agencies. [3] Discussion Here, correlation probably is causation, as climate precedes the other three variables in causality, and again because these are unlikely to be genetic differences that reflect adaptation to different environments -- one of the few cases where natural selection "has not had enough time." An objection is that the differences could reflect a "brain drain," whereby smart people flock to colder states, and their smart children boost the state's NAEP scores. Even in this case, where climate does not cause group differences in IQ, it still confirms the hypothesis that colder climates favor civilization -- why else would smarties flock there? But I doubt this anyway, since Montana, Wyoming, and North and South Dakota are not exactly fonts of civilization that smarties pour into, yet they have White IQs on par with the highly developed New York City metro area. If it is causation, as seems likely, the mechanism could be anything. Pathogen load is surely part of it, hence the fields of study called "tropical disease" and "tropical medicine." Also, you might sweat too much in hotter environments, bringing you closer to dehydration. As mild as these effects may seem, when accumulated over the course of development, they could result in your body spending more resources on bodily maintenance than on luxury items like IQ and toil. Heat could also just make you more fatigued -- that wouldn't affect IQ, but it would affect your work ethic, making you less likely to complete college and more likely to pursue quick fixes like crime to get what you want. The correlation is stronger for getting a college degree than performance on 8th grade math and science tests, and that could be because college work is more g-loaded, because it also taps into work ethic aside from IQ, and because out-of-staters show up in the college figures but not the 8th grade figures. As tough as the environment may seem to natives, it must seem unbearable to college students raised in a different climate. To the best of my knowledge, as the saying goes, this is the first demonstration of an association between climate type and IQ, civilization-related achievement, and crime, even among a population that's pretty homogenous genetically (for the traits of interest, at least). Even what genetic diversity there is among Whites would underestimate the effect -- Whites adapted to hotter environments, such as Italians and Greeks, are far more concentrated in the colder states within the US. To put the final nail in the coffin, though, you'd want to look at babies of Whites who are adopted into White families in a state of noticeably different temperature than that of the biological parents. Still, it seems pretty unavoidable: hotter environments are less conducive to civilization, at least for Whites, and not just in extreme cases like the failed attempt to colonize sub-Saharan Africa. Civilization may have started in hot areas, but that was then. It apparently flourishes much more in colder climates. Just as we provide iodine in table salt to prevent a nutrient deficiency from lowering IQ, it might be just as well to encourage people to settle colder areas. It's not like they'd be abandoning civilization -- just the opposite. They could take their accents, music, and whatever else with them, but they would not suffer the environmental insults that lower their group's IQ, lower their ability to get a college degree, and make them more likely to commit crime. Fortunately for them -- and unfortunately for current residents -- the Mountain states have incredibly low population densities and could absorb some Whites from hotter states. That would certainly burden the locals for a generation, but again since lower White IQ in the Southeast is probably due to largely treatable environmental causes, it won't take long for them to contribute as citizens on the same level as the locals. Notes [1] Underlying this is likely a tendency for all sorts of things to be more migratory in such environments -- winged insects were chosen because there's lots of solid data to illustrate the point. Basically, environments that are highly unstable favor migratory features since your environment may go from good to bad from one day to the next, or from one spot to the next -- and being able to quickly move on to greener pastures will be well worth it. When environmental quality does not change much in space or time, then the expensive wings (or whatever) will not pay off. [2] If you don't have statistical software, you can do a lot for free on Wessa.net, including correlation. [3] Although I didn't run a test of normality on the distributions for temperature, iq, degrees, or crime, I did check the skewness of all, and only crime was significantly skewed: for crime, skewness is +2.1 standard errors of skewness (SES); for temperature, +1.24 SES; for degrees, +0.35 SES; and for IQ, -1.51 SES. Addendum from Razib: I put up a related post at my other weblog. Labels: civilization, climate, crime, education, IQ, true redneck stereotypes
Monday, July 14, 2008
Steve's review of Grand New Party is up. He suggests that much of GNP is laced with Sailerian wisdom; I think that's a fairly plausible point, though Ross & Reihan might claim other sources for the derivation of particular observations or datum. I've read about 3/4 of Grand New Party. I don't talk much about politics because I don't feel like I know much about it, and frankly, I don't allocate many cognitive cycles to the topic (though I do follow politics via my RSS, it's mostly a passive pursuit). Nevertheless, I've liked GNP mostly because the argument and perspective is relatively thickly scaffolded with data which is of a fundamentally apolitical character. I can say the same of one of the few other political books I've read in the past year, Brink Lindsey's Age of Abundance. I'll be putting up a review of GNP at my other weblog soon; I suspect it'll be the first positive review of a right-wing book on Scienceblogs, so I'll count myself a trailblazer after I click "post"!
Update: Ross clarifies (I found the UK working class descriptions to be the sore thumb as well). Labels: politics
Saturday, July 12, 2008
It's fun to read association studies published in Cell; the molecular biology community generally takes a massively different path to an association than the current "big science" approach of massive genome-wide studies. Case in point: a recent paper identifying a non-synonymous variant in a previously unannotated gene associated with late-onset Alzheimer's disease.
The approach the authors took was this: linkage studies had identified a region of chromosome 10 as potentially harboring a potential Alzheimer's variant, and the hippocampus is among the first tissues affected by the disease. Thus, genes located in the chromosome 10 region and highly expressed in the hippocampus are potential candidates. There are a whole host of reasons you can come up with to convince yourself that this has no chance of working, but in this case, it did. The authors identified a transcript that fit their profile, but of course, there was absolutely nothing known about it. So they painstakingly characterized it as a calcium channel and identified a common non-synonymous polymorphism in it that's associated with Alzheimer's in several different cohorts. To top it off, they show evidence that the SNP changes the activity of the channel. Overall, quite an impressive piece of work.
Friday, July 11, 2008
Stephen Bainbridge weighs in on the side of wine in its role as a catalyst for Civilization. The authors of He said Beer, She Said Wine engage in a more proximately relevant debate....
Labels: Finn baiting
Thursday, July 10, 2008
In Scientific American. If you've been following this site, it's old hat to you, but still.
Via ALDaily. Labels: Population genetics
Wednesday, July 09, 2008
Some sources/influences on my previous post, and my thinking in general, are listed below. I'm not recommending that everyone run off and buy all of these books, but they might pique your curiosity. Of course, to the extent one has time, it's always good to read and re-read the classic h-bd/evolutionary psychology writers such as Herrnstein & Murray, Sailer, Pinker, Dawkins, Dennet, and E.O. Wilson.
I consider all of these works, as those of Murray, Sailer, Pinker, Plomin et. al. to be good examples of what George Orwell called "the empirical habit of thought," which I believe is critical to understanding human diversity and defeating what Godless Capitalist termed the "Death Star 2.0" [see comments] version of PC. In fact, all the books below except (perhaps) for the textbook Multivariate Data Analysis make what are at least crypto pro-hbd statements. As an aside, one problem with crimethinking is that it tends to be decentralized and hard to find, much less to unite and make use of. Thus, I think it is useful to "think outside the box" in terms of finding pro h-bd works and thinkers. Descartes' Error--Antonio Damasio Spiritual Evolution--George Vaillant The Wisdom of the Ego--George Vaillant The Natural History of Alcoholism: Revisited--George Vaillant What You Can Change and What you Can't--Martin E.P. Seligman Multivariate Data Analysis--Hair et. al. 1984--George Orwell Comment: O'Brien in 1984 spookily reminds me of Richard Lewontin and his disturbing capacity for doublethink and goodthinkfulness (i.e. willingness to swallow and propagate orthodoxy in the face of well-known facts, such as Lewontin's denying race and genetic influences on behavior in spite of his rather extensive knowledge of genetics and population genetics in particular). Lewontin strikes me as the kind of person who, if he were in power, would force people to be "re-educated" for speaking of the biological basis for human behavior, while unknown to the public, promoting the study of pharmacology, gene therapies, and genetic engineering as tools to increase his power and the power his pseudo-socialist State. In fact, the potential usefulness of biotechnology as a mind control tool is the one thing that makes me have some misgivings about it (though I am still very much in favor of the advancement of biotech). Labels: Books, crimethink, Evolutionary Psychology, human biodiversity
Have multiple intelligence theories really been disproven?
posted by
birch barlow @ 7/09/2008 04:46:00 PM
[this is a slightly edited version of what was originally a haloscan comment]
I have come to believe that it is crucial to realize that there are other factors in intelligence besides g and its subfactors (e.g. math/performance, visuospatial, verbal, short-term memory). This is important not only factually and scientifically, but politically as well; a less g/traditional IQ-based theory of intelligence and human biodiversity is probably both more accurate and more politically palatable than a heavily g-centered one. The main drawback is that such a theory is also unfortunately quite complicated and difficult to test. Many apparently non-g factors are almost certainly correlated with g, but they are not the same thing. In terms of higher-visibility phenomena, this would mean factors like creativity, motivation/drive, consistency, effective planning. In terms of lower-visibility phenomena, this would mean factors such as (neocortical) left brain/right brain ability, efficiency, and interconnectedness, as well as the interaction of such entities with the paleomammalian/limbic/midbrain and reptilian/lower brain/brain stem. The main problem, in my opinion, is that these factors other than g are much harder to measure, and virtually impossible to measure on a 3-hour test, much less a brain scan (given current technology). Of course there are self-report tests for personality, creativity, motivation, and the like, but self-report tests are not, in general, terribly reliable. Also, insightful multivariate data analysis and effective experimental design for such analysis is hard to come by because these tasks are extremely difficult for even an intelligent person (in both the g and non-g sense) to carry out. Thus the failure of "multiple intelligence" theories in spite of the fact that it is clear that there are multiple intelligences. If you are still unconvinced, how else would one explain a 25-year old with a 150 IQ, but also with Asperger's Syndrome/autism spectrum disorder, living on the streets while a 90-IQ illegal immigrant is living reasonably comfortably, and an intellectually uncurious and largely vacuous (outside of the classroom/lab/workplace) individual with only a 115 IQ is living large?(if you want a picture of the latter individual, think of Julia from (Orwell's) 1984 transplanted to the real America ca. 2008, or the devoted Asian [1] college student who seems to always be studying (high motivation/drive/tolerance for long, boring tasks) but has no intellectual interests and spends most of her/his [2] free time with sleazy entertainment, sleeping around, smoking pot, drinking, and popping pills [3]). Of course social factors such as biases against more autistic personalities may be partially at work, but most stereotypes and social biases have *some* basis in reality, even if they all too often facilitate cruelty and inefficiency. It is also important to remember that biological phenomena can lead to social phenomena (e.g. autistics, due to their biology, are repelled by (and repel) others, leading to a negative social reputation for autistics) just as environmental/social phenomena can lead to biological phenomena (e.g. autistics, due to their negative social reputation, increasingly have their biology wired for being hermits). [1] and [2] Being intelligent but uncurious seems to be substantially more common amongst Asians (and perhaps amongst high-IQ blacks and Hispanics/Amerinds as well) than whites, and more common amongst females than males. This is only my personal observation, and it may be an entirely sociocultural phenomenon even if it is real. [3] Nothing against sleeping around, smoking pot, drinking, or popping pills, but these don't tend to be the most intellectual activities in the world, in spite of common protestations to the contrary by horny drug users (such as, admittedly, myself) to the contrary. Also, I realize that immigrant (and particularly Asian) cultures are strongly biased against such hedonistic behaviors, but this bias tends to quickly fade amongst the children of immigrants, and even more so their grandchildren, as they become more modernized, Westernized, and Americanized. Labels: crimethink, human biodiversity, Philosophy of science, Psychology
Tuesday, July 08, 2008
Slate has been having a debate on sex differences. Along the way, they hit on a key Summers issue: The apparent higher male variability of math scores. Shaffer, the author, refers to the classic Feingold piece, a cross-cultural meta-study of the variability of mental abilities across genders. Shaffer makes the common claim that there are data on both sides--sometimes women have a higher variance, and sometimes the men do. But is the difference statistically significant?
I did a simple analysis of Feingold's data from 54 math tests from 20 countries, and 19 tests of spatial ability from 9 countries. I ran least squares and least absolute deviation tests. Here are the p-values for the restriction that men and women have equal variability: Math, least squares: p<0.1% Math, least absolute deviation: p<5% Spatial, least squares: p<10% Spatial, least absolute deviation: p=11% (but only 19 observations!) OK, so it's reasonable to conclude that men have higher variability in this cross country sample, and that the cases of greater female variability are just flukes. But are the differences quantitatively significant, not just statistically significant? Feingold, the author of the study, says no. He notes: "The median V[ariance]R[atio] of 1.09 indicated greater male variability [on math tests]," then claims that "the magnitude of the gender difference was trivial." Not so. Excel will show you that three or four standard deviations above the mean--Larry Summers territory to be sure--that's enough to get you a 2-to-1 one ratio. And that's with no difference in means whatsoever. This paper (Table 1, page 10) works out the rough gender ratios you'd expect to see under various assumptions for means and variances. The bottom line is no surprise: with small differences in means plus small differences in variance, you can get big results: 4 to 1 ratios are easy to come by, and 10 to 1 are plausible. Yes, yes, further research is needed, but most of the research is pointing in the same direction. And we Bayesians know what to do when research mostly points in one direction.... (Oh, and the median male/female variance ratio for spatial ability in Feingold's data is 1.14. And yes, none of this gets at genes v. culture. But let's start with the journalism before we head to causation.) Labels: Larry Summers, sex differences
Monday, July 07, 2008
Sunday, July 06, 2008
Maxim's audience prefers brunettes; distribution is bimodal
posted by
agnostic @ 7/06/2008 03:10:00 PM
While showing that the super-popularity of blonds is recent, I saw an apparent reversal of the upward trend around 2000, suggesting that perhaps Playboy readers are becoming fatigued by blonds. To get a better feel for what the younger generations prefer, let's look at Maxim magazine (US edition), whose average reader is 27.5 years old (by contrast, the average Playboy reader is 32.5). Maxim is the contemporary counterpart to Playboy -- it's widespread on college campuses, and is what horny dudes are likely to leaf through to ogle hot babes. They also have roughly the same circulation -- about 2.5 million. For those in a rush, I've boldfaced all key results.
Audacious Epigone and I have both done analyses on the Maxim Hot 100 lists for recent years (see here and here). But these smell of "lists just for the fun of making lists" or "lists to get people arguing," and the fact that A.E.'s results and mine varied so much despite analyzing consecutive years supports that idea. However, there are at least two datasets that are surely more shaped by audience demand than the editors' whims: the girls who appear on the cover to lure the reader into purchasing it (they are featured prominently inside as well), and the girls who readers vote as being the hottest out of a pool of "Hometown Hotties" nominees. First, I looked at all covers of Maxim from 1997 to present, excluding only two issues that did not show people, which yielded 126 covers. To be more fine-grained than before, I coded hair color as 1 = light blond, 2 = dark blond, 3 = light brown, 4 = dark brown, and set aside 0 for redheads. If there were multiple girls on a cover, or if an issue had multiple covers available, I took the average of all girls for that issue. For a few, it was too close to call, so I coded the girl halfway between two categories. If the cover was ambiguous, I looked at the full photo shoot through a Google Images search. There was no significant trend in blondness over the past 11 years. To determine the average hair color, I re-coded redheads as 2.5 (there were only 2 of 126, so this choice doesn't really make a difference). The average Maxim cover girl scores 2.8 -- light brown. To determine the frequency distribution, I binned girls into light blond, dark blond, light brown, and dark brown, with redheads going into the light brown bin. Some data-points were not integers, so I used both conventions for rounding the numbers with .5 ("up" and "down"). It turned out to make almost no difference. Here is the distribution using "rounding up": Light blonds and dark browns are overrepresented, while the intermediate colors are underrepresented. To test this, I used published data on hair color frequencies and took the Dutch values instead of the Icelandic ones, since Americans must resemble the former more than the latter. Because the published estimates have only one intermediate category, I had to merge the dark blond and light brown categories together. I put redheads in the intermediate category since otherwise I wouldn't be able to do a chi-squared test (an expected number would be too small). For rounding up, chi-squared = 24.1 (p less than 0.0001, df = 2); and for rounding down, chi-squared = 27.4 (p less than 0.0001, df = 2). So, the discrepancy between Maxim cover girls and the general population is no fluke. But are light blonds and dark browns equally overrepresented? No: depending on the rounding convention, light blonds are 25-29% more common than we'd expect, whereas dark browns are 63-66% more common than we'd expect. Together with the average cover girl being light brown, I conclude that Maxim readers respond more to women with dark hair, although there is a sizable minority that prefers light hair. Second, I did a similar analysis on the finalists in Maxim's Hometown Hotties contest from 2003 to 2007. For 10 weeks each year, Maxim staffers scour the country to photograph 100 local hotties per week. Of these 100, Maxim readers vote online to determine 10 semi-finalists and 1 finalist for that week. There is no way I'm looking through 5000 pictures to see what all the contestants look like, and the 5 winners are too small of a sample. The 50 finalists seem like enough data to get a good picture. (Someone else can analyze all 500 semi-finalists.) Indeed, the results are virtually identical to the cover girl results, which shows that both datasets are reliably measuring the same thing. The methods are as before. Here is the distribution of hair types among Hometown Hotties finalists: Once more, light blonds and dark browns are overrepresented, while intermediate colors are underrepresented. For rounding up, chi-squared = 10.3 (p = 0.0058, df = 2); for rounding down, chi-squared = 13.1 (p = 0.0014, df = 2). These results are no fluke. As before, though, dark browns are more overrepresented than light blonds: by 57-64% compared to 22-52%, respectively, depending on the rounding convention. (The convention for rounding didn't make much of a difference overall in these data either, but since the sample size is less than half that of the cover girl data, it introduces more uncertainty.) Replicating the cover girl results, the average Hometown Hotties finalist scores 2.8 -- light brown. I conclude what I did in the cover girl case. To see how closely the two datasets agree with each other, I did a chi-squared test for the observed values in one, using the other's frequencies as the expected ones. Taking the cover girl frequencies as expected, the hometown hotties data are no different (chi-squared = 0.025, p = 0.9875, df = 2). The same holds for the other way around (chi-squared = 0.068, p = 0.9666, df = 2). That is for rounding up, but rounding down produced p-values above 0.5 as well. I conclude that both datasets measure the same thing -- audience preferences. As a final anecdote in support of the bigger picture, consider the Miss Maxim girls. Although about 1/2 of the 24 countries could have easily supplied a blond, only 1/6 actually did. The girls from Belgium, England, and so on, look quite different from the average Belgian, Englishwoman, etc. Clearly, among Maxim's horndog audience, dark hair rules. What is causing these two key results -- that Maxim readers prefer brunettes, and that the distribution is bimodal? I think brunettes are just more exciting on the level of physiological arousal, so the younger -- and therefore the randier -- the audience is, the more they will prefer dark hair. When Playboy's circulation was growing exponentially in the 1960s, it featured hardly any blonds and mostly brunettes. As its average reader has become older, its Playmates have become blonder. Lighter hair is correlated with behavioral inhibition (see here), so it could also be that dark-haired girls get the blood pumping more because they appear more flirtatious. Or it may be a pure fashion trend -- digging blonds is what your father's generation did, so you set yourselves apart by tacking up pictures of Mila Kunis and Vanessa Minnillo on your wall. As for the bimodal nature of the distribution, this probably reflects supply meeting demand: the audience's preferences are likely bimodal, with a majority preferring brunettes and a minority preferring blonds. Guys respond better to the exaggerated version of their tastes, and that drives up the fraction of light blonds and dark browns, in the same way that among porn stars you see an inflated fraction of women with large breasts or large rumps. Labels: babes and hunks, Pigmentation
Saturday, July 05, 2008
Ben G in the comments points to COMMON GENETIC VARIANTS UNDERLYING COGNITIVE ABILITY, a dissertation. I don't have time to read the whole thing right now, but comments welcome.
Labels: Genomics
Will genetic testing lead to the downfall of private insurance?
posted by
Razib @ 7/05/2008 11:30:00 AM
That's what Daniel is asking at Genetic Future, and he is soliciting the input of the economically informed. I've closed comments on this post so as to encourage you to leave comments there if you have something intelligent to say. Also, Dan posted last year. FWIW I am moderately skeptical of health benefits for the average person re: genomics as I recall several years back steakhouses were supposedly attributing their robust business to the ubiquity of statins. I suspect quantitative improvements in healthcare will have more relevance toward combining lifestyle choices with the current expectations of life expectancy and quality of life as opposed to pushing the longevity window outward much. The ubiquity of fatitude makes me skeptical that we're going in any direction aside from risking-pooling. BTW, Half Sigma has recently been promoting socialized medicine.
Friday, July 04, 2008
I assume most readers know about SNPedia, but I started noticing some traffic from it recently, so it must be gaining some traction.
Thursday, July 03, 2008
Continuing my series of notes on Sewall Wright's population genetics, I come to the subject of migration. This is important in understanding the differences between Wright and R. A. Fisher on the role of genetic drift in evolution. Fisher and Wright both agreed that genetic drift would be too weak a process to be of evolutionary significance in large populations (above, say, 10,000 in effective size) . [Note 1] Equally, they agreed that it would be important in small populations, provided these remained sufficiently isolated over sufficiently long periods of time. Their disagreement was over the probability that the necessary degree of isolation would occur. This depends largely on the rate of migration between populations.
Fisher's views on the subject can be pieced together from scattered remarks, as I attempted here. It seems that from an early stage - at least from his 1921 review of the 'Hagedoorn Effect' - Fisher regarded small isolated populations as unimportant in evolution. If they stayed isolated for long, they would go extinct from occasional adverse conditions (epidemic disease, drought, etc). If they did not stay isolated, the flow of migrants from outside (whether in a steady small trickle, or occasional larger floods) would be sufficient to prevent their gene frequencies from drifting far from those of the general population of their species. But so far as I know, Fisher never made any formal quantitative estimate of the amount of migration necessary to offset genetic drift. Sewall Wright, on the other hand, did make such estimates, and developed them in published works from 1931 onwards. It is known that a first draft of Wright's major 1931 paper on 'Evolution in Mendelian Populations') was written as long ago as 1925. In this he already took the view that genetic drift in small semi-isolated populations was an important evolutionary factor. This might suggest that by that time he had already considered the role of migration in depth. The draft of 1925 has not survived (Provine p. 237), but it seems that in fact it did not yet contain a detailed treatment of migration. The evidence for this is from Wright's correspondence with Fisher in 1929. Wright told Fisher that 'since I wrote [in August 1929, sending a copy of his draft] I have been trying to get a clearer idea of the effect of diffusion [i.e. migration] and I see, at least, that isolation in districts must be much more nearly complete than I realized at first, to permit random fixation of strains' [Provine p.256]. This conclusion is presented more formally in 'Evolution in Mendelian Populations' (at ESP pp.127-9). Here Wright develops an equation for the distribution of gene frequencies which incorporates a term for m, the rate of migration into a small semi-isolated population from a larger population with different gene frequencies. The exact meaning of this equation is difficult to interpret [see Note 2], but Wright's own conclusion is that 'Where m [the migration rate] is less than 1/2N [with N being the effective size of the receiving population] there is a tendency toward chance fixation of one or the other allelomorph [i.e. one of the alleles at a locus where there are two alleles in the population]. Greater migration prevents such fixation. How little interchange appears necessary to hold a large population together may be seen from the consideration that m = 1/2N means an interchange of only one individual every other generation, regardless of the size of the subgroup'. This conclusion has been widely restated in the population genetics literature. Unfortunately I do not know of any clear and mathematically elementary proof. (John Maynard Smith [p. 158-60] presents a proof using only basic algebra, but it combines the treatment of migration and mutation, and involves various simplifying assumptions and approximations. There are also some confusing misprints or slips of the pen.) It may be surprising that the rate of migration sufficient to prevent populations drifting apart can be stated as a constant number of migrants, regardless of the size of the population. D. S. Falconer comments that 'This conclusion, which may at first seem paradoxical, may be understood by noting that a smaller population needs a higher rate of immigration than a larger one to be held at the same state of dispersion' [Falconer p.79]. We may put this point slightly more formally by noting that the effect of migration in offsetting drift may be expected to be proportional to the rate of migration. The rate can be expressed as n/N, where n is the number of migrants and N is the effective size of the receiving population. Since the effect of genetic drift has previously been shown to be proportional to 1/2N, we can therefore expect the migration rate required to neutralise drift to be n/N = k/2N, where k is some constant factor of proportionality. But it follows that in equilibrium we will have n = k/2, where k is a constant. Of course, this does not tell us the size of k, but it is plausible that it is of the order of 1, as is proved by Wright and others using more rigorous methods. The conclusion that only around 1 migrant every other generation is sufficient to prevent sub-populations drifting apart might seem fatal to Wright's belief in the importance of genetic drift. As shown in his correspondence with Fisher, Wright does initially seem to have had his confidence shaken. But Wright (like Fisher) was not one to give up a cherished theory without a struggle. Immediately following the quoted passage from 'Evolution in Mendelian Populations', Wright continues: 'However, this estimate must be qualified by the consideration that the effective N [the population size] of the formula is in general much smaller than the actual size of the population or even than the breeding stock, and by the further consideration that qm ['m' is a subscript, indicating the frequency of the allele among the migrants] of the formula refers to the gene frequency of actual migrants and that a further factor must be included if qm is to refer to the species as a whole. Taking both of these into account, it would appear that an interchange of the order of thousands of individuals per generation between neighboring subgroups of a widely distributed species might well be insufficient to prevent a considerable random drifting apart in their genetic compositions' (ESP p.128). Wright's first point, that effective N may be lower than the apparent size of the population, is either confused or confusing, since Wright has just proved that N, the effective size of the receiving population, is irrelevant to the number of immigrants required to neutralise drift. Perhaps Wright is thinking of the effective number of migrants, rather than of the receiving population, in which case the number who succeed in contributing to the gene pool may indeed be less than the total number. The second point is valid, but not well explained. Wright's formula contains a term mqm (with the second m a subscript), where qm is the frequency of the relevant allele among the migrants. But the underlying assumption is that this is the same as in the species generally. Wright's point (made more explicitly in later papers) is that the allele frequencies in neighbouring populations are likely to be more similar than in the species generally, so that mqm will actually be less than is assumed in the derivation of the result. To adjust for this we might stipulate that the 'effective' number of migrants is smaller than the actual number, even of those who successfully breed, just as the 'effective' population size may be smaller than the actual size. This approach is clearer in later papers, for example at ESP p.236: 'Cross breeding is, however, most likely to be with neighboring populations which differ but little in value of q. In this case the coefficient m is only a small fraction of the actual amount of change [i.e. the actual observed rate of migration]'. With this adjustment of mqm, the number of actual migrants required to neutralise drift might indeed be many more than 1 per generation. This is valid as far at it goes, but it depends on the assumption that allele frequencies in neighbouring populations are likely to be relatively similar. This is perfectly plausible, but only because we tacitly assume that migration between neighbouring subpopulations is, or recently has been, sufficient to offset genetic drift. Wright therefore seems perilously close to sawing off the branch he is sitting on. Certainly, if the allele frequencies do drift 'considerably' apart (to use Wright's word in 'Evolution in Mendelian Populations'), the assumption of similar frequencies ceases to apply, and we can no longer rely on it. A further consideration is that on an evolutionary time scale (i.e. hundreds or thousands of generations) occasional larger influxes of migrants are almost bound to occur, and undo all the slow work of genetic drift. Even if an allele is lost or fixed in a subpopulation, it can be reintroduced at any time by migration from outside, so long as it persists somewhere in the species. Wright continued to study the effect of migration after 1931, with his fullest treatment in the paper 'Isolation by Distance' in 1943 (ESP pp.401-425). Here Wright examines three different models for migration: the Island Model, in which migrants are derived at random from a number of semi-isolated subpopulations of the species, and therefore on average have the gene frequencies of the species as a whole; isolation by distance in a two-dimensional continuum, where the probability of cross-breeding is proportional to the distance between the birthplaces of the breeding individuals; and isolation by distance in a linear range such as a river-bank. Wright's conclusions from the Island Model are not very different from those in his 1931 paper based on the cruder assumption of random migration throughout the species. The conclusions from two-dimensional isolation by distance are only slightly more favourable. As he summarises it in 1943: 'It is apparent that there is a great deal of local differentiation if the random breeding unit is as small as 10, even within a territory the diameter of which is only ten times that of the unit. If the unit has an effective size of 100, differentiation becomes important only at much greater relative distances. If the effective size is 1000, there is only slight differentiation at enormous distances. If it is as large as 10,000 the situation is substantially the same as if there were panmixia [random mating] throughout any conceivable range' (ESP p.411). Only for the more special linear-range model is there substantial differentiation due to drift in populations of moderate size. Wright's theoretical conclusions might seem to imply that genetic drift in subpopulations would seldom be a major factor in evolution. It seems to require rather special circumstances to be effective: either very small populations, populations sparsely scattered with long distances between them, populations with a narrow linear range, or organisms that are very immobile at all stages of their life cycle. Wright nevertheless continued to insist throughout his career that drift in subpopulations was an important, if not essential, feature of evolution. The uncharitable view of this would be that Wright was simply stubborn. Having taken up his position on the importance of this factor, before having considered in depth the effects of migration, he was determined to defend it. come what may. (There would be a parallel here with the equally stubborn position of Fisher on the evolution of dominance.) A more charitable view would be that Wright was trying to find an explanation of something that was generally accepted by biologists when he began his career: namely, that the observable differences between subspecies, and even between species, are usually selectively neutral. Wright himself stresses this point in 'Evolution in Mendelian Populations': 'It appears, however, that the actual differences among natural geographical races and subspecies are to a large extent of the nonadaptive sort expected from random drifting apart. An interesting example, apparently nonadaptive, is the racial distribution of the 3 allelomorphs which determine human blood groups' (ESP p.128). In the years and decades following 'Evolution in Mendelian Populations', the opinion of biologists turned away from the consensus view in 1931 (really no more than a superficial assumption) that subspecific differences are selectively neutral. Much of the relevant research was carried out by the students and collaborators of Wright and Fisher themselves, notably E. B. Ford in England and Theodosius Dobzhansky in the USA. The general outcome was that even apparently minor subspecific differences often had some selective value. Human blood groups, for example, were found to be correlated with resistance to different diseases, though it remains unclear whether all such differences have a selective basis. The importance of genetic drift in subpopulations is of course an empirical matter. It is quite possible that some species are 'Wrightian' and some are 'Fisherian' in this respect. The observed amount of genetic diversity between subpopulations is usually quite modest (Maynard Smith p.160-161], suggesting that migration between them is usually sufficient to prevent them drifting far apart . There are theoretical reasons for expecting that 'Fisherian' species would be in a majority. Most species have adaptations for dispersal at some stage of their life. Plants, for example, have adaptations for spreading their seeds. Among animals, the juveniles of one or both sexes often disperse from their region of birth to find mates or territories. With a few exceptions, organisms that just stick to one spot are doomed to extinction within a fairly short period of evolutionary time, since the conditions of life seldom stay fixed for many generations. Even in species with relatively stable environments, there are theoretical reasons for expecting that a mixture of mobility and immobility would be adaptive (W. D. Hamilton, Narrow Roads of Gene Land, vol. 1, chapter 11). But it remains possible that 'Wrightian' processes are important in some cases. A particularly interesting case is the modern human species itself. After the dispersal of modern humans out of Africa, it is likely that human populations for most of the last 100,000 years were small and scattered, with little migration between different continental groups. These are good conditions for Wrightian genetic drift. Whether the observed differences in gene frequencies between continental populations are due to drift or selection remains an active area of research [see Jobling et al., passim]. Note 1. Neither Wright nor Fisher were very interested in genetic drift among genetic variants that are selectively entirely neutral, as expounded in Kimura's theory of neutral evolution at the molecular level. Fisher died before Kimura published his theory. Wright lived long enough to take account of it, and found it plausible enough with regard to neutral mutations of nucleotides, but considered it of no evolutionary interest (see Provine p.469-77). Note 2. As I understand it, Wright's conception of the distribution of gene frequencies is broadly is follows. We assume that two populations have evolved separately, and are fixed for different alleles at one or more loci. (For simplicity it is assumed that there are no more than two alleles at each locus.) The two populations are then combined and interbreed freely. Assuming that the populations are of equal size, the frequencies of the alleles at each locus in the combined population will initially all be 50%. The combined population then evolves in isolation. As a result of random genetic drift, the allele frequencies will tend to drift away from 50%. Over a large number of loci (or over a large number of hypothetical populations) we can ask, what is the probability that an allele will have any particular frequency after any specified number of generations? The total of such probabilities over all possible allele frequencies, from 0 to 1, will of course add up to 1, and will have an approximately smooth (continuous) distribution, which (on the given assumptions) will be symmetrical around a frequency of 50%. Initially the probability distribution will be clumped closely around 50%, but as time goes on it will spread out. Eventually, some alleles will begin to be lost or fixed, with a probability of 1/2N per generation. Wright now assumes that beyond a certain number of generations the shape of the probability distribution of frequencies for the remaining alleles will be approximately constant, apart from the continuing occasional loss and fixation of alleles, which will affect all the remaining alleles equally. The problem is to find this constant distribution under various assumptions about mutation, migration, and selection. Much of Wright's work in the 1930s was devoted to this problem. I cannot claim to have followed Wright's derivations in detail, as his explanations are obscure even by his usual standards. The problem is not just that the mathematics is advanced (though it does involve more calculus than in most of Wright's work) but that he makes various simplifying assumptions and approximations which are not self-evidently justified. I can only take it on trust that the conclusions are correct, and that if they were not (as Dobzhansky put it) 'some mathematician would have found it out'. References: [Provine] William B. Provine: Sewall Wright and Evolutionary Biology, 1986. [ESP] Sewall Wright: Evolution: Selected Papers, edited and with Introductory Materials by William B. Provine, 1986. D. S. Falconer: Introduction to Quantitative Genetics, 3rd edn., 1989. M. Jobling, M. Hurles, and C. Tyler-Smith: Human Evolutionary Genetics, 2004. John Maynard Smith: Evolutionary Genetics, 1989. Labels: Burbridge, Population genetics
Wednesday, July 02, 2008
In discussions of nature vs. nurture a common assumption is that if it is in the genes then we can't fix it. Or we can only change it by eugenics or bioengineering babies. I wish to suggest a different approach.
The following links provide background: Bioengineered Stem Cells Rejuvenate Muscles In Mice Stem Cell Review Series: Aging of the skeletal muscle stem cell niche Stem Cell Review Series: Regulating highly potent stem cells in aging: environmental influences on plasticity Autism-spectrum disorder reversed in mice Essentially all tissues turn-over with time. Some tissues such as the gut lining are replaced every three days, other tissues such as bone and fat are replaced over decades. (Proven by tracking green florescent cell markers over time.) In the adult brain, neurons are seldom replaced but new neurons are continually produced and some repair occurs. I believe it will eventually be shown that all tissues contain stem cells that have the potential to rebuild that tissue. Pluripotent hematopoietic stem cells from bone marrow can, with the proper differentiation signals, produce every cell type in the body. Stem cells make up less than 1/10,000 of the cells in tissue. (Adipose tissue may have a higher frequency of stem cells. Satellite cells in muscle tissue may also be relatively common. I welcome correction if I'm wrong about other tissue types.) If scientists could replace that small stem cell fraction and increase the rate of cell turn-over then eventually most of the body cells would become the new type. Each day a few hundred stem cells in the bone marrow mobilize, circulate in the blood, and either migrate to specific tissue sites, resettle into other bone marrow niches, or die. (This has been observed in mice by florescent labeling of transplanted stem cells.) By injecting a few thousand stem cells each day, a person's original bone marrow stem cells could be gradually replaced. The process would be accelerated if stem cell mobilizing drugs were used. Or if the old stem cells were selectively targeted for destruction. By itself, transplants using young stem cells don't significantly repair damage or rejuvenate tissue. Proper signals are needed to mobilize the stem cells to the desired site, to cause the stem cells to divide, to cause the stem cells to differentiate into the right cells, and to cause those cells to integrate into the existing tissue. This is what happens when our body successfully heals a wound. For rejuvenation scientists also need to kill senescent cells and remodel the extracellular matrix. This isn't easy but significant progress is being made. Imagine that in ten years the technology existed to completely replace the stem cells in one mouse with stem cells from a different mouse. And that the tissue turn-over rate was increased so that most of the mouse body cells derived from the second mouse. How much remodeling of body and brain would occur? Some body structures would have been largely fixed during development but much would change due to the new cell DNA. Potentially, a sick or dull mouse could be made healthy or smart by such a full body stem cell makeover. In addition there will be progress in restructuring damaged parts of the brain. This may require putting the tissues back in an earlier developmental state so as to rebuild a functional structure, e.g., regrow a nerve fiber connection. Memories stored in the original brain tissue structure would be lost but functionality would be regained after training. Even developmentally fixed traits might be altered by selective rebuilding of body structures. The stem cell donors might be world class athletes, handsome, musically gifted, with IQ's over 160. By expanding a cell line in culture, one donor could supply an unlimited number of recipients. Modest genetic engineering might improve the cell line. Even the germ cells would be replaced so future offspring would not be genetically related to the original person. Would you choose to undergo such a metamorphosis? Externally you might change in just a couple of years. Your parents and friends might not recognize you. Internally you should have pretty much the same memories. However, your internal processing might be different and your personality might change. I think you would feel like the same person but you would also know that you were different. Like remembering how it felt to be depressed...you were you then and you are you now but you aren't the same you. Hopefully your spouse would like the new you. This would be a little like massive cosmetic surgery. This is a potential solution to the unfair distribution of good genetic traits. It could be a win-win for all groups. Defeat old age, class divisions, and racial strife in one stroke. I would do it to myself and would support having the government offer free treatment to everyone. It might even be offered as an alternative to execution or long term imprisonment. Labels: life hacking, Stem cells
Recent advances in genotyping have made genome-wide association studies the standard way to study the genetics of a phenotype in humans (model organisms, for various reasons, are suddenly lagging behind). In terms of simply identifying loci underlying disease, this approach has led to a number of notable successes, but there's been a nagging concern that identifying loci of small effect doesn't help much with diagnostics--even with 30 loci now know to impact height, genetics is able to account for something like 3% of the total variance in the phenotype despite the fact that the heritability of the trait is something like 90%.
Different traits have different genetic architectures, of course, so the recent publication of 30 loci involved in Crohn's disease has led to vastly different results: To advance gene discovery further, we combined data from three studies on Crohn's disease (a total of 3,230 cases and 4,829 controls) and carried out replication in 3,664 independent cases with a mixture of population-based and family-based controls. The results strongly confirm 11 previously reported loci and provide genome-wide significant evidence for 21 additional loci, including the regions containing STAT3, JAK2, ICOSLG, CDKAL1 and ITLN1. So with the same number of loci, how much of the variance are these authors able to explain? It's 10%, a modest number, but larger than that currently mapped for most (any?) other complex trait. And keeping in mind that the heritability of Crohn's disease is estimated at 50%, they've accounted for something like a fifth of the total genetic variance. I'm not sure exactly what threshold makes genetics clinically useful, but surely this is approaching it. Labels: Genetics
Trait-Like Brain Activity during Adolescence Predicts Anxious Temperament in Primates. ScienceDaily summary:
We all know people who are tense and nervous and can't relax. They may have been wired differently since childhood.
PLoS stays afloat with bulk publishing: Science-publishing firm struggles to make ends meet with open-access model. In Nature News.
When The Inductivist observed that the unchurched tend more toward criminality, I asked whether social matrix would be a major factor here. In other words, in an area where church going is a major signal of social conformity antisocial oddballs would be far more likely to break the the norm. With a follow up The Inductivist says:
My next step was to estimate the association between arrest and attendance for each of the nine divisions: I did this with logistic regression (sample sizes ranged between 460 and 2,306). I then calculated the Pearson correlation between these logit coefficients and the mean attendance scores displayed above. It is .44. This means that the connection between arrest and never going to church is stronger in areas where churchgoing is most common. So Razib might be right that in religious areas many of the well-adjusted folks feel like they should go to church, leaving a high percentage of antisocial people among the ranks of non-attenders. A meta-point here (and obvious one to many of you no doubt) is that religion can not be understood simply as a relationship between an individual and their faith in an atomic manner. The social dimension in critical to mass religion. Related: Good Without God, But Better With God?
Tuesday, July 01, 2008
|



