|
Saturday, February 06, 2010
Two new papers are out in PLoS Biology which make inferences about adaptation using butterfly species which exhibit Mullerian mimicry. I'll give the author summaries instead of the abstracts.
Genomic Hotspots for Adaptation: The Population Genetics of Mullerian Mimicry in the Heliconius melpomene Clade: The diversity of wing patterns in Heliconius butterflies is a longstanding example of both Mullerian mimicry and adaptive radiation. The genetic regions controlling such patterns are "hotspots" for adaptive evolution, with small regions of the genome controlling major changes in wing pattern. Across multiple hybrid zones in Heliconius melpomene and related species, we no find no strong population signal of recent selection. Nonetheless, we find significant associations between genetic variation and wing pattern at multiple sites. This suggests patterning alleles are relatively old, and might be a better model for most natural adaptation, in contrast to the simple genetic basis of recent human-induced selection such as pesticide resistance. Strikingly, across the region controlling the red forewing band, a very strong association with phenotype implicates three genes as potentially being involved in control of wing pattern. One of these, a kinesin gene, shows parallel differences in expression levels between divergent forms in the two mimetic species, making it a strong candidate for control of wing pattern. These results show that mimicry involves parallel changes in gene expression and strongly suggest a role for this gene in control of wing pattern. Genomic Hotspots for Adaptation: The Population Genetics of Mullerian Mimicry in Heliconius erato: Identifying the genetic changes responsible for beneficial variation is essential for understanding how organisms adapt. Here, we use a combination of mapping, population genetic analysis, and gene expression studies to identify the genomic regions responsible for phenotypic evolution in the Neotropical butterfly Heliconius erato. H. erato, together with its co-mimic H. melpomene, have undergone parallel and concordant radiations in their warningly colored wing patterns across Central and South America. The "genes" underlying the H. erato color pattern radiation are classic examples of Mendelian loci of large effect and are under strong natural selection. Nonetheless, we do not see a clear molecular signal of recent natural selection, suggesting that the H. erato color pattern radiation, or the alleles that underlie it, may be quite old. Moreover, rather than being single locus, the genetic patterns suggest that multiple, widely dispersed loci may underlie pattern variation in H. erato. One of these loci, a kinesin gene, shows parallel expression differences between races during wing pattern formation in both H. erato and H. melpomene, suggesting that it plays an important role in pattern variation. High rates of recombination within naturally occurring H. erato hybrid zones mean that finer genetic dissection will allow us to localize causative sites and better understand the history and molecular basis of this extraordinary adaptive radiation. Here's a section from the first paper which I found intriguing: The results therefore appear to support the 'shifting balance' model for the evolution of Heliconius colour pattern races...whereby novel wing patterns arise and spread through otherwise continuous populations behind moving hybrid zones...The 'Pleistocene refuge' model seems less likely, as recent contact after extended periods of geographic isolation would presumably have left a stronger signal of genetic differentiation between divergent races, perhaps across the genome but especially more strongly in regions linked to patterning loci... I have no idea why they necessarily think this validates the shifting balance. You can see David's critique of the model, but reading Will Provine's intellectual biography of Sewall Wright it seems that the shifting balance sometimes becomes the evolutionary genetic version of "it's complicated."* What they seem to have done here though is refute a simple model of powerful selective sweeps giving rise to these morphs recently. Rather, these seem to be ancient local adaptations, whose frequencies and genetic architectures are perhaps perturbed by long term exogenous (e.g., environment) and endogenous (e.g., complex frequency dependencies) dynamics. Despite my lack of clarity on a few theoretical issues, I found the papers very interesting, and haven't really processed them fully. Citation: Baxter SW, Nadeau NJ, Maroja LS, Wilkinson P, Counterman BA, et al. 2010 Genomic Hotspots for Adaptation: The Population Genetics of Mullerian Mimicry in the Heliconius melpomene Clade. PLoS Genet 6(2): e1000794. doi:10.1371/journal.pgen.1000794 Counterman BA, Araujo-Perez F, Hines HM, Baxter SW, Morrison CM, et al. 2010 Genomic Hotspots for Adaptation: The Population Genetics of Mullerian Mimicry in Heliconius erato. PLoS Genet 6(2): e1000796. doi:10.1371/journal.pgen.1000796 * I see one reference to epistasis in both papers, and that concept is very important in the shifting balance. Though I assume the LD and supergenes might point to that. Labels: Population genetics
Sunday, January 24, 2010
Frequency of lactose malabsorption among healthy southern and northern Indian populations by genetic analysis and lactose hydrogen breath and tolerance tests:
Volunteers from southern and northern India were comparable in age and sex. The LTT result was abnormal in 88.2% of southern Indians and in 66.2% of northern Indians...The lactose HBT result was abnormal in 78.9% of southern Indians and in 57.1% of northern Indians...The CC genotype was present in 86.8% and 67.5%...the CT genotype was present in 13.2% and 26.0%...and the TT genotype was present in 0% and 6.5%..of southern and northern Indians, respectively. The frequency of symptoms after the lactose load...and peak concentrations of breath hydrogen...both of which might indicate the degree of lactase deficiency, were higher in southern than in northern Indians. 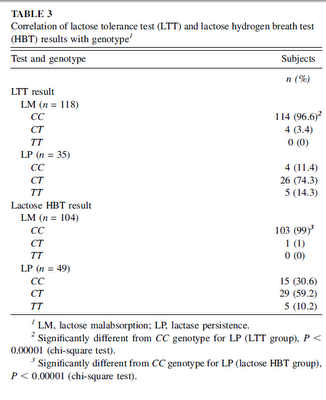 The north Indian samples were from Lucknow on the mid-Gangetic plain, and the south Indian samples from Bangalore. The genetic variant conferring lactase persistence is the Central Asian one, T-1390. You can see the distribution of the genotypes by phenotype in the table to the left. These authors assume that the T allele was brought by the Indo-Aryans; this seems plausible seeing its clinal variation, as well the fact that this variant seems to be common in European and Central Asian populations. The frequency of the T allele in the Lucknow sample was 39%, and 13% in the Bangalore sample. Here are a selection of frequencies for the T allele in other populations: The north Indian samples were from Lucknow on the mid-Gangetic plain, and the south Indian samples from Bangalore. The genetic variant conferring lactase persistence is the Central Asian one, T-1390. You can see the distribution of the genotypes by phenotype in the table to the left. These authors assume that the T allele was brought by the Indo-Aryans; this seems plausible seeing its clinal variation, as well the fact that this variant seems to be common in European and Central Asian populations. The frequency of the T allele in the Lucknow sample was 39%, and 13% in the Bangalore sample. Here are a selection of frequencies for the T allele in other populations:17% - Saami You can see more here. This looks like a case of local adaptation. Labels: India, Population genetics
Monday, January 18, 2010
John Hawks has some commentary on a Nicholas Wade article which previews a new paper on long term effective population size in humans, soon to be out in PNAS (Wade's piece states that it'll be out tomorrow, but it's PNAS). Wade states:
They put the number at 18,500 people, but this refers only to breeding individuals, the "effective" population. The actual population would have been about three times as large, or 55,500. Assuming an average census size on the order of 50,000, it seems as if our species stumbled onto a rather "risky" strategy of avoiding extinction. From what I recall conservation biologists start to worry about random stochastic events (e.g., a virulent disease) driving a species to extinction once its census size reaches 1,000. I suppose the fact that we were spread out over multiple continents would have mitigated the risk, but still.... It also brings me back to my post from yesterday, it seems that for most of human history we are a miserable species on the margins of extinction. For the past 10,000 years we were a miserable species. And now a substantial proportion of us are no long miserable (it seems life is actually much improved from pre-modern Malthusianism outside of Africa and South Asia). If only Leibniz could have seen it! Labels: Population genetics
Saturday, January 09, 2010
Localizing recent positive selection in humans using multiple statistics
posted by
p-ter @ 1/09/2010 07:41:00 AM
Online this week in Science, a group presents a method for identifying genes under positive selection in humans, and gives some examples. I have somewhat mixed feelings about this paper, for reasons I'll get to, but here's their basic idea:
Readers of this site will likely be familiar with genome-wide scans for loci under positive selection in humans (see, eg., the links in this post). In such a scan, one decides on a statistic that measured some aspect of the data that should be different between selected loci and neutral loci--for example, extreme allele frequency differences between populations, or long haplotypes at high frequency--and calculates this statistic across the genome. One then decides on some threshold for deciding a locus is "interesting", and looks at those loci for patterns--are there genes involved in particular phenotypes among those loci? Or protein-coding changes? In this paper, the authors note that many of these statistics are measuring different aspects of the data, such that combining them should increase power to distinguish "interesting" loci from non-"interesting" loci. That is, if there's an allele at 90% frequency in Europeans and 5% frequency in Asians, that's interesting, but if that allele is surrounded by extensive haplotype structure in one of those populations, that's even more interesting. The way they combine statistics is pretty straightforward--they essentially just multiply together empirical p-values from different tests as if they were independent. I wouldn't believe the precise probabilities that come out of this procedure (for one, the statistics aren't really fully independent), but it seems to work--in both simulations of new mutations that arise and are immediately under selection and in examples of selection signals where the causal variant is known (Figures 1-3)--for ranking SNPs in order of probability of being the causal SNP underlying a selection signal. With this, the authors have a systematic approach for localizing polymorphisms that have experienced recent selection. It's necessarily somewhat heuristic, sure, but it does the job. They then want to apply this procedure to gain novel insight into recent human evolution. This is sort of the crux of the matter--does this new method actually give us new biological insight? The novel biology presented consists of a few examples of selection signals where they now think they've identified a plausible mechanism for the selection--a protein-coding change in PCDH15, and regulatory changes near PAWR and USF1 (their Figure 4). On reflection, however, these examples aren't new. Consider PCDH15--this gene was mentioned in a previous paper by the same group, where they called a protein-coding change in the gene one of the 22 strongest candidates for selection in humans (Table 1 here, and main text). It's unclear what is gained with the new method (except perhaps to confirm their previous result?). Or consider the regulatory changes near PAWR and USF1. The authors use available gene expression data to show that SNPs near these genes influence gene expression, and that the signals for selection and the signals for association with gene expression overlap. Early last year, a paper examined in detail the overlap between signals of this sort, and indeed, both of these genes are mentioned as examples where this overlap is observed. So using different methods, a different group published the same conclusion about these genes a year ago. Again, it's unclear what one gains with this new method. In general, then, this paper has interesting ideas, but puzzlingly fails to really take advantage of them [1]. That said, they've taken some preliminary steps down a path that is very likely to yield interesting results in the future. ----- [1] I wonder if I'm being too harsh on this paper just because it was published in a "big-name" journal. If this were published in Genetics, for example, I certainly wouldn't be opining about whether or not it contains any novel biology. ----- Citation: Grossman et al. (2010) A Composite of Multiple Signals Distinguishes Causal Variants in Regions of Positive Selection. Science. DOI: 10.1126/science.1183863 Labels: Population genetics
Sunday, December 20, 2009
Different Evolutionary Histories of the Coagulation Factor VII Gene in Human Populations?:
Immoderate blood clotting constitutes a risk factor for cardiovascular disease in modern industrialised societies, but is believed to have conferred a survival advantage, i.e. faster recovery from bleeding, on our ancestors. Here, we investigate the evolutionary history of the Coagulation Factor VII gene (F7) by analysing five cardiovascular-risk-associated mutations from the F7 promoter and nine neutral polymorphisms (six SNPs and three microsatellites) from the flanking region in 16 populations from the broader Mediterranean region, South Saharan Africa and Bolivia (687 individuals in total). Population differentiation and selection tests were performed and linkage disequilibrium patterns were investigated. In all samples, no linkage disequilibrium between adjacent F7 promoter mutations ŌłÆ402 and ŌłÆ401 was observed. No selection signals were detected in any of the samples from the broader Mediterranean region and South Saharan Africa, while some of the data suggested a potential signal of positive selection for the F7 promoter in the Native American samples from Bolivia. In conclusion, our data suggest, although do not prove, different evolutionary histories in the F7 promoter region between Mediterraneans and Amerindians. The primary aim of this research seems to have been to figure out if the variance in a medical trait (prevalence in cardiovascular disease) could be traced to variance in this coagulation factor gene. Doesn't seem like that panned out. But their "Native American" sample happened to consist of Bolivian highlanders, Quechua and Aymara speakers. There are long haplotypes amongst these populations for the variant which seems result in increased risk for cardiovascular disease. I don't know much about physiology, but I immediately wondered if modulating traits which effect hematological system might have nasty side-effects. The populations of the Andes of course have developed some genetic tricks to optimize their functioning at high altitudes, bt tricks often have trade-offs. Of course this doesn't necessarily mean it's selection which drove up the frequency of the variant in question. Native populations of the New World seem to have gone through a population bottleneck, which can generate some of the same patterns. But there are enough non-highland groups whereby one could check to see if they have the high risk variant and a long haplotype as well. Labels: Medicine, Population genetics
Thursday, December 10, 2009
Stable Patterns of Gene Expression Regulating Carbohydrate Metabolism Determined by Geographic Ancestry:
Methodology/Principal Findings  Figure 2 had me thinking of Me, Myself & Irene. Figure 2 had me thinking of Me, Myself & Irene.Labels: Genetics, Population genetics
Wednesday, November 25, 2009
Two new articles in AJHG, Genomic Dissection of Population Substructure of Han Chinese and Its Implication in Association Studies:
To date, most genome-wide association studies (GWAS) and studies of fine-scale population structure have been conducted primarily on Europeans. Han Chinese, the largest ethnic group in the world, composing 20% of the entire global human population, is largely underrepresented in such studies. A well-recognized challenge is the fact that population structure can cause spurious associations in GWAS. In this study, we examined population substructures in a diverse set of over 1700 Han Chinese samples collected from 26 regions across China, each genotyped at Ōł╝160K single-nucleotide polymorphisms (SNPs). Our results showed that the Han Chinese population is intricately substructured, with the main observed clusters corresponding roughly to northern Han, central Han, and southern Han. However, simulated case-control studies showed that genetic differentiation among these clusters, although very small (FST = 0.0002 Ōł╝0.0009), is sufficient to lead to an inflated rate of false-positive results even when the sample size is moderate. The top two SNPs with the greatest frequency differences between the northern Han and southern Han clusters (FST > 0.06) were found in the FADS2 gene, which associates with the fatty acid composition in phospholipids, and in the HLA complex P5 gene (HCP5), which associates with HIV infection, psoriasis, and psoriatic arthritis. Ingenuity Pathway Analysis (IPA) showed that most differentiated genes among clusters are involved in cardiac arteriopathy (p < 10ŌłÆ101). These signals indicating significant differences among Han Chinese subpopulations should be carefully explained in case they are also detected in association studies, especially when sample sources are diverse. And, Genetic Structure of the Han Chinese Population Revealed by Genome-wide SNP Variation: Population stratification is a potential problem for genome-wide association studies (GWAS), confounding results and causing spurious associations. Hence, understanding how allele frequencies vary across geographic regions or among subpopulations is an important prelude to analyzing GWAS data. Using over 350,000 genome-wide autosomal SNPs in over 6000 Han Chinese samples from ten provinces of China, our study revealed a one-dimensional ŌĆ£north-southŌĆØ population structure and a close correlation between geography and the genetic structure of the Han Chinese. The north-south population structure is consistent with the historical migration pattern of the Han Chinese population. Metropolitan cities in China were, however, more diffused ŌĆ£outliers,ŌĆØ probably because of the impact of modern migration of peoples. At a very local scale within the Guangdong province, we observed evidence of population structure among dialect groups, probably on account of endogamy within these dialects. Via simulation, we show that empirical levels of population structure observed across modern China can cause spurious associations in GWAS if not properly handled. In the Han Chinese, geographic matching is a good proxy for genetic matching, particularly in validation and candidate-gene studies in which population stratification cannot be directly accessed and accounted for because of the lack of genome-wide data, with the exception of the metropolitan cities, where geographical location is no longer a good indicator of ancestral origin. Our findings are important for designing GWAS in the Chinese population, an activity that is expected to intensify greatly in the near future. Labels: Chinese, Genetics, Han, Population genetics
Tuesday, November 24, 2009
Carl Zimmer reports that it might be a function of physics. Bigger whales have proportionality bigger mouths, but at some point the biological engineering runs up against constraints:
s they report today in the Proceedings of the Royal Society, Goldbogen and his colleagues found that big fin whales are not just scaled-up versions of little fin whales. Instead, as their bodies get bigger, their mouths get much bigger. Small fin whales can swallow up about 90% of their own body weight. Very big ones can gulp 160%. In other words, big fin whales need more and more energy to handle the bigger slugs of water they gulp. As their body increases in size, the energy their bodies demand rises faster than the extra energy they can get from their food. Given enough time and a large population one can imagine that evolution might be able to figure out a solution, or back out of the adaptive dead end. Labels: Evolution, Genetics, Population genetics
Monday, November 23, 2009
A a new paper in PLoS ONE, Genetic Variation and Recent Positive Selection in Worldwide Human Populations: Evidence from Nearly 1 Million SNPs:
Our analyses both confirm and extend previous studies; in particular, we highlight the impact of various dispersals, and the role of substructure in Africa, on human genetic diversity. We also identified several novel candidate regions for recent positive selection, and a gene ontology (GO) analysis identified several GO groups that were significantly enriched for such candidate genes, including immunity and defense related genes, sensory perception genes, membrane proteins, signal receptors, lipid binding/metabolism genes, and genes involved in the nervous system. Among the novel candidate genes identified are two genes involved in the thyroid hormone pathway that show signals of selection in African Pygmies that may be related to their short stature. They seem to have looked at about twice as many SNPs by combining the sets of Illumina and Affymetrix chips as the norm. But they looked at only around 1/4 the number of individuals as other studies which used the HGDP panel. To a first approximation the Affy and Illumina chips are really close in the patterns of variation which they detect, but, the Illumina chip had a significantly higher heterozygosity (this is evident in some of the supplementals just by inspection).  I reformatted a figure which shows ancestral contributions to the individuals in their sample at K = 6 (6 hypothetical populations which contribute to genetic variation). In the paper they discuss the fact that the Uyghur and Hazara resemble each other, and that the Uyghur seem to have a non-trivial Central/South Asian component, and finally that the Russian and Adygei have East Asian and Central/South Asian ancestry. None of this is surprising, all this was evident in other papers which used the same sample. I reformatted a figure which shows ancestral contributions to the individuals in their sample at K = 6 (6 hypothetical populations which contribute to genetic variation). In the paper they discuss the fact that the Uyghur and Hazara resemble each other, and that the Uyghur seem to have a non-trivial Central/South Asian component, and finally that the Russian and Adygei have East Asian and Central/South Asian ancestry. None of this is surprising, all this was evident in other papers which used the same sample.First, in regards to Russians, analysis of genetic variation among East European populations sometimes show a "long tail" of variation which leads toward East Asia among Russians. That is, Russians tend to cluster with other Europeans, but a minority of individuals are deviated in the direction of East Asians, that minority shrinking in proportion to distance from Europeans. The historical reason for this presents itself plainly: a significant minority of ethnic Russians have Tatar antecedents in the recent past, and of those who do not such ancestry may be derived from Slavicized Finno-Ugric populations who may have ancient connections to the populations of Siberia. The Russian Orthodox priest who was murdered last week known for preaching to Muslims was himself an ethnic Tatar by origin. Second, one should expect the Uyghur and Hazara to resemble each other. The Hazara likely emerged during the period of Mongol rule of Iran and Afghanistan, and are descendants in part of Mongols and Turks from greater Mongolia who settled down in Afghanistan. The Uyghurs are a Turkic-speaking people, but historically the Tarim Basin was inhabited by Europoid populations. The emergence of the Uyghur and Hazara mimic each other almost perfectly. In particular, the East Asian component of their ancestry is from the same region. The non-East Asian aspect differs a bit, but not too much when set next to the East Asian component. Interestingly, the Uyghur speak a Turkic language, while the Hazara speaking Dari, the Persian dialect. One can probably chalk that up to distance from the Turco-Mongol ur-heimat. Third, the Central/South Asian component among the Uyghur should not be too surprising, there is significant evidence that the Tarim basin was influenced by Indo-Iranians, as well as the Tocharians. Buddhism arrived in East Asia via the Tarim Basin after all, and there have always been trade routes from the southern edge of the Tarim down into northern India. But what about the Russians and the Adygei? I think that this signal has something to do with what we've termed elsewhere as "Ancestral North Indians" (ANI), who were closely related to European populations, and probably emerged from somewhere in Eastern Europe to Central Asia. I've been told that the Fst number for ANI-Northern European populations is on the order of the distance between Baltic peoples and southern Italians. So this group may have emerged on the margins of Europe, and expanded mostly within Asia.  There's also an interesting chart showing patterns of selection, or at least what they detected, across geographies. Even if most of the signals are false positives one may hold that the real signals within this subset will still recapitulate the geographic relationships shown to the left. The patterns of selection mirror overall phylogenetic relationships. Note the overlap patters of Central/South Asians with Europeans and East Asians, some of both, but dominated by the former. There's also an interesting chart showing patterns of selection, or at least what they detected, across geographies. Even if most of the signals are false positives one may hold that the real signals within this subset will still recapitulate the geographic relationships shown to the left. The patterns of selection mirror overall phylogenetic relationships. Note the overlap patters of Central/South Asians with Europeans and East Asians, some of both, but dominated by the former. Citation: Lopez Herraez D, Bauchet M, Tang K, Theunert C, Pugach I, et al. 2009 Genetic Variation and Recent Positive Selection in Worldwide Human Populations: Evidence from Nearly 1 Million SNPs. PLoS ONE 4(11): e7888. doi:10.1371/journal.pone.0007888 Labels: Genetics, Population genetics
Friday, November 20, 2009
A new provisional paper, Ancestry-related assortative mating in latino populations. Here are the results:
Using 104 ancestry informative markers, we examined spouse correlations in genetic ancestry for Mexican spouse pairs recruited from Mexico City and the San Francisco Bay Area, and Puerto Rican spouse pairs recruited from Puerto Rico and New York City. In the Mexican pairs, we found strong spouse correlations for European and Native American ancestry, but no correlation in African ancestry. In the Puerto Rican pairs, we found significant spouse correlations for African ancestry and European ancestry but not Native American ancestry. Correlations were not attributable to variation in socioeconomic status or geographic heterogeneity. Past evidence of spouse correlation was also seen in the strong evidence of linkage disequilibrium between unlinked markers, which was accounted for in regression analysis by ancestral allele frequency difference at the pair of markers (European versus Native American for Mexicans, European versus African for Puerto Ricans). We also observed an excess of homozygosity at individual markers within the spouses, but this provided weaker evidence, as expected, of spouse correlation. Ancestry variance is predicted to decline in each generation, but less so under assortative mating. We used the current observed variances of ancestry to infer even stronger patterns of spouse ancestry correlation in previous generations.  The correlations are to the left. An interesting point is that the correlations of total genome content seem too high to be explained by assortative mating for salient physical features (skin color, hair form, etc.) alone. From the text: The correlations are to the left. An interesting point is that the correlations of total genome content seem too high to be explained by assortative mating for salient physical features (skin color, hair form, etc.) alone. From the text:Another possibility involves physical characteristics, such as skin pigment, hair texture, eye color, and other physical features. Certainly, these traits are correlated with ancestry and are likely to be factors in mate selection. However, the spouse correlation for these traits must be high and the correlation of these traits with ancestry must also be high to explain the observed ancestry correlations.... As noted above, they controlled for SES and geography, and the correlation remains. Looking at the correlations within the genomes of these individuals they also inferred that assortative mating in the past was actually greater than it is today (they also have a historical citation which suggests this). I wonder of the correlation of ancestry is due to sorting by many traits which are subtle and nuanced, and relatively difficult to capture in surveys of the coarse salient traits are used to categorize phenotypic races. Looking at many traits, as opposed to a few, and one would have a better sense of total genome content. When it comes to mating one might look to a range of traits which in other circumstances are not noted, or fall below the threshold of reflective awareness. I'm assuming there might be something here which is Gestalt and subconscious. Kind of like the various studies which attempt to correlate mate preferences by HLA polymorphism. Labels: Genetics, Population genetics
Sunday, November 08, 2009
Common Variants in the Trichohyalin Gene Are Associated with Straight Hair in Europeans:
Hair morphology is highly differentiated between populations and among people of European ancestry. Whereas hair morphology in East Asian populations has been studied extensively, relatively little is known about the genetics of this trait in Europeans. We performed a genome-wide association scan for hair morphology (straight, wavy, curly) in three Australian samples of European descent. All three samples showed evidence of association implicating the Trichohyalin gene (TCHH), which is expressed in the developing inner root sheath of the hair follicle, and explaining ~6% of variance (p = 1.5 X 10-31). These variants are at their highest frequency in Northern Europeans, paralleling the distribution of the straight-hair EDAR variant in Asian populations. This sort of stuff has obvious applications forensics. Labels: Population genetics
A genome-wide study of common SNPs and CNVs in cognitive performance in the CANTAB:
Psychiatric disorders such as schizophrenia are commonly accompanied by cognitive impairments that are treatment resistant and crucial to functional outcome. There has been great interest in studying cognitive measures as endophenotypes for psychiatric disorders, with the hope that their genetic basis will be clearer. To investigate this, we performed a genome-wide association study involving 11 cognitive phenotypes from the Cambridge Neuropsychological Test Automated Battery. We showed these measures to be heritable by comparing the correlation in 100 monozygotic and 100 dizygotic twin pairs. The full battery was tested in 750 subjects, and for spatial and verbal recognition memory, we investigated a further 500 individuals to search for smaller genetic effects. We were unable to find any genome-wide significant associations with either SNPs or common copy number variants. Nor could we formally replicate any polymorphism that has been previously associated with cognition, although we found a weak signal of lower than expected P-values for variants in a set of 10 candidate genes. We additionally investigated SNPs in genomic loci that have been shown to harbor rare variants that associate with neuropsychiatric disorders, to see if they showed any suggestion of association when considered as a separate set. Only NRXN1 showed evidence of significant association with cognition. These results suggest that common genetic variation does not strongly influence cognition in healthy subjects and that cognitive measures do not represent a more tractable genetic trait than clinical endpoints such as schizophrenia. We discuss a possible role for rare variation in cognitive genomics. David Goldstein is one of the authors. I wonder if this influenced his views on the evolution of intelligence. Labels: Association, IQ, Population genetics
Friday, October 30, 2009
Something that has been nagging me about the recent paper by Reich et al. which models Indian populations as a hybridization event between two ancestral groups, "Ancestral South Indians" (ASI) and "Ancestral North Indians" (ANI). As a reminder, the ANI seem to have been rather like Europeans in their allele frequencies, or at least far closer to Europeans than they were to the ASI (it seems that they compared ANI with Western Europeans). This is interesting. They found in the populations surveyed that the low bound for ANI was 40%, the high ~80% (in the supplements they included some Pathans and Sindhis from the HGDP, and that's where that number comes from). The ~40% low bound for ANI rather surprised me. The populations which they sampled included South Indian tribal groups. In other words, these were the groups arguably least affected by what we term Hinduism and Indian culture (their status as "tribals" as opposed to lower caste or outcaste was generally a function of the fact that they rejected integration and assimilation into mainstream Indian culture and isolated themselves both geographically and in terms of their customs). Just seems weird that these groups would be so ANI.
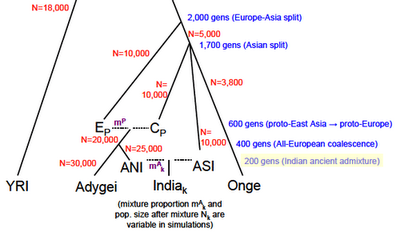 For a few weeks now Greg Cochran has been asking if I saw something in the paper above about when the admixture between ANI and ASI occurred, or at least if there was a hint about when the authors think it occurred. I said no, there are only hints. I was wrong, I skimmed over the supplement too quickly, they assume 200 generations ago as a parameter in a model they use for simulations. Bingo. Just click the image to the left, and look at the lower right. 200 generations = 5,000 years ago, assuming 25 years for generation time. Let's assume that a South Indian tribal group is a small deme of ASI surrounded by a very large (infinite) deme of ANI for 200 generations. If I assume a constant outmarriage rate of 0.25% per generation (1 out of 400) then at the present time you'd have the tribal group being ~40% ANI. For a few weeks now Greg Cochran has been asking if I saw something in the paper above about when the admixture between ANI and ASI occurred, or at least if there was a hint about when the authors think it occurred. I said no, there are only hints. I was wrong, I skimmed over the supplement too quickly, they assume 200 generations ago as a parameter in a model they use for simulations. Bingo. Just click the image to the left, and look at the lower right. 200 generations = 5,000 years ago, assuming 25 years for generation time. Let's assume that a South Indian tribal group is a small deme of ASI surrounded by a very large (infinite) deme of ANI for 200 generations. If I assume a constant outmarriage rate of 0.25% per generation (1 out of 400) then at the present time you'd have the tribal group being ~40% ANI.OK, what about my idea which I presented to John Hawks that Indians "don't really look" like a hybridization between Northern Europeans and the ASI, ASI assumed to be similar to the Andaman Islanders (who I do not believe were necessarily "Negritos," insofar as I suspect their small stature is due to contact with Europeans and Indians, as those who have avoided such contact are seen to be of normal or even above average size for South Asians). Specifically the frequency of light eyes and hair is just way too low among groups which are on the 70-80% ANI range such as Punjabis and Kashmiris, though these groups do tend have more Caucasoid features and lighter (olive) skin. On the other hand, here is something which jumped out at me about the Reich et al. paper: they added two Pakistani populations who fit well in the ANI-ASI cline which most of the Indian groups mapped onto (some groups with "Eastern" origin in both Pakistan and India were discarded from the analysis), and their ANI frequency proportions seemed familiar to me. There are three ANI estimates for both groups: Sindhi - 78%, 70.7%, 73.7% (78%) Pathan - 81%, 74.2%, 76.9% (81%) In the parenthesis is the frequency for the derived (European-like) variant of SLC24A5. The data sets were the same, from the HGDP, though the ancestry estimates used only 10 and 15 of the approximately 50 of each group respectively. There's a suspicious correspondence here. The lowest frequency of the derived variant of SLC24A5 I've seen for a South Asian population is ~30% for Sri Lankan Tamils, with ~50% for Sri Lankan Sinhalese. Remember that a reasonable low bound for ANI for South Asian groups is on the order of 40%. But what about my contention that other European-like pigmentation alleles don't fit because the phenotype isn't what you'd expect. You can look at a blue vs. brown eye variant of OCA2 in the HGDP. Another eye color variant, HERC2. And here is a variant of TYR which causes light skin. The interesting point would be to look at the Indian samples, but I don't have really good proxies for that (in one paper which surveyed Indian Americans various language groups ranged from 70-100% in derived SLC24A5 frequency, but it is very difficult to imagine that these correspond well to many groups in the Reich paper. Specifically, it's biased toward higher status/caste groups). I might have spoken too soon, though it still seems to me that something is off. Perhaps Europeans changed after ANI left. Or perhaps ANI changed when it arrived in India. One recent data point which I find curious is that a paper just came out which suggests that populations of the Andronovo culture in Trans-Siberia, which is assumed to be the precursor to the Indo-Iranians, seem to resemble modern day Russians in pigment phenotype. At least judging from the genes extracted and sequenced. More later when my thoughts become more settled. Labels: India, Population genetics
Friday, October 23, 2009
Enhanced Edar Signalling Has Pleiotropic Effects on Craniofacial and Cutaneous Glands:
The skin carries a number of appendages, including hair follicles and a range of glands, which develop under the influence of EDAR signalling. A gain of function allele of EDAR is found at high frequency in human populations of East Asia, with genetic evidence suggesting recent positive selection at this locus. The derived EDAR allele, estimated to have reached fixation more than 10,000 years ago, causes thickening of hair fibres, but the full spectrum of phenotypic changes induced by this allele is unknown. We have examined the changes in glandular structure caused by elevation of Edar signalling in a transgenic mouse model. We find that sebaceous and Meibomian glands are enlarged and that salivary and mammary glands are more elaborately branched with increased Edar activity, while the morphology of eccrine sweat and tracheal submucosal glands appears to be unaffected. Similar changes to gland sizes and structures may occur in human populations carrying the derived East Asian EDAR allele. As this allele attained high frequency in an environment that was notably cold and dry, increased glandular secretions could represent a trait that was positively selected to achieve increased lubrication and reduced evaporation from exposed facial structures and upper airways. Every explanation for the "classic Mongoloid" phenotype seems to go back to "cold and dry." Some things never change. Labels: Population genetics
If you haven't been following the goings-on via Twitter, Luke Jostins has been posting some tidbits on his blog, Genetic Inference. If you get interested in something, remember you can search abstracts.
Labels: Genetics, Population genetics
Very interesting paper in PLoS Genetics, Inferring the Joint Demographic History of Multiple Populations from Multidimensional SNP Frequency Data. Here's the author summary:
The demographic history of our species is reflected in patterns of genetic variation within and among populations. We developed an efficient method for calculating the expected distribution of genetic variation, given a demographic model including such events as population size changes, population splits and joins, and migration. We applied our approach to publicly available human sequencing data, searching for models that best reproduce the observed patterns. Our joint analysis of data from African, European, and Asian populations yielded new dates for when these populations diverged. In particular, we found that African and Eurasian populations diverged around 100,000 years ago. This is earlier than other genetic studies suggest, because our model includes the effects of migration, which we found to be important for reproducing observed patterns of variation in the data. We also analyzed data from European, Asian, and Mexican populations to model the peopling of the Americas. Here, we find no evidence for recurrent migration after East Asian and Native American populations diverged. Our methods are not limited to studying humans, and we hope that future sequencing projects will offer more insights into the history of both our own species and others. And from the abstract: We infer divergence between West African and Eurasian populations 140 thousand years ago (95% confidence interval: 40-270 kya). This is earlier than other genetic studies, in part because we incorporate migration. We estimate the European (CEU) and East Asian (CHB) divergence time to be 23 kya (95% c.i.: 17-43 kya), long after archeological evidence places modern humans in Europe. Finally, we estimate divergence between East Asians (CHB) and Mexican-Americans (MXL) of 22 kya (95% c.i.: 16.3-26.9 kya), and our analysis yields no evidence for subsequent migration. I would keep in mind these 95% confidence intervals, but I immediately wondered about this European-East Asian divergence time just like Dienekes. Labels: Genetics, Population genetics
Monday, October 12, 2009
A genome-wide meta-analysis identifies 22 loci associated with eight hematological parameters in the HaemGen consortium:
The number and volume of cells in the blood affect a wide range of disorders including cancer and cardiovascular, metabolic, infectious and immune conditions. We consider here the genetic variation in eight clinically relevant hematological parameters, including hemoglobin levels, red and white blood cell counts and platelet counts and volume. We describe common variants within 22 genetic loci reproducibly associated with these hematological parameters in 13,943 samples from six European population-based studies, including 6 associated with red blood cell parameters, 15 associated with platelet parameters and 1 associated with total white blood cell count. We further identified a long-range haplotype at 12q24 associated with coronary artery disease and myocardial infarction in 9,479 cases and 10,527 controls. We show that this haplotype demonstrates extensive disease pleiotropy, as it contains known risk loci for type 1 diabetes, hypertension and celiac disease and has been spread by a selective sweep specific to European and geographically nearby populations. In ScienceDaily: By comparing human data with genetic data from chimpanzees, the team were able to conclude that the genetic variant was the result of a selection event favouring variants that increase the risk of heart disease, coeliac disease and type 1 diabetes in European populations 3,400 years ago. The authors suggest that the risk factors were positively selected for because they gave carriers an increased protection against infection. This sort of disease-based pleiotropy is of course interesting because disease really bites. On the other hand, I think other many interesting phenotypes are out there which probably emerged due to pleiotropy. East Asian hair and European eye color are two guesses. Looking for these clusters of traits associated with one genotype might be a nice way to crank-down the probability of an adaptive-story. Labels: Population genetics
Friday, October 09, 2009
Evolution with Stochastic Fitness and Stochastic Migration:
As has previously been shown with selection, the role of migration in evolution is determined by the entire distributions of immigration and emigration rates, not just by the mean values. The interactions of stochastic migration with stochastic selection produce evolutionary processes that are invisible to deterministic evolutionary theory. I haven't read the paper yet, but on my "To-Read" list.... Labels: Population genetics
Wednesday, September 30, 2009
Identification of Copy Number Variants Defining Genomic Differences among Major Human Groups:
Overall, our results provide a comprehensive view of relevant copy number changes that might play a role in phenotypic differences among major human populations, and generate a list of interesting candidates for future studies. The discussion is a little heavy on how the results might have errors...caution! Here's the PCA:  (if you're reading this weblog, I assume you know what "CEU" refers to and such) Labels: Population genetics
Sunday, September 27, 2009
Neutrophil Response to Dental Plaque by Gender and Race:
The inflammatory response, which has both genetic and environmental components, is a central mechanism linking oral and systemic diseases. We hypothesized that dental plaque accumulation over 21 days in the experimental gingivitis model would elicit systemic inflammatory responses [change in white blood cell (WBC) count and neutrophil activity], and that these responses would differ by gender/race. We recruited 156 healthy young adults, including black and white males and females. Plaque Index (PI), Gingival Index (GI), systemic WBC counts, and peripheral neutrophil oxidative activity were recorded. Overall, 128 participants completed the study. During the experimental phase, the correlation between PI and GI was 0.79. Total WBC and neutrophil counts did not change. Neutrophil activity increased in blacks but not whites, suggesting that there may be racial differences in the inflammatory response to dental plaque accumulation. Don't genes like DARC track the nature of inflammatory response? And don't those genes exhibit a lot of African/non-African difference? Pointers, corrections and thoughts welcome in the comments. Labels: Population genetics
Thursday, August 27, 2009
As most readers of this weblog know most humans as adults cannot digest lactose. The ability to digest lactose via the persistence of the enzyme lactase is differentially distributed. Both inferential methods and a small number of ancient genetic extractions suggest that this ability arose within the last 10,000 years. A new paper, The Origins of Lactase Persistence in Europe:
Most adults worldwide do not produce the enzyme lactase and so are unable to digest the milk sugar lactose. However, most people in Europe and many from other populations continue to produce lactase throughout their life (lactase persistence). In Europe, a single genetic variant, ŌłÆ13,910*T, is strongly associated with lactase persistence and appears to have been favoured by natural selection in the last 10,000 years. Since adult consumption of fresh milk was only possible after the domestication of animals, it is likely that lactase persistence coevolved with the cultural practice of dairying, although it is not known when lactase persistence first arose in Europe or what factors drove its rapid spread. To address these questions, we have developed a simulation model of the spread of lactase persistence, dairying, and farmers in Europe, and have integrated genetic and archaeological data using newly developed statistical approaches. We infer that lactase persistence/dairying coevolution began around 7,500 years ago between the central Balkans and central Europe, probably among people of the Linearbandkeramik culture. We also find that lactase persistence was not more favoured in northern latitudes through an increased requirement for dietary vitamin D. Our results illustrate the possibility of integrating genetic and archaeological data to address important questions on human evolution. Here's a graphical illustration of their conclusion:  Labels: Genetics, Population genetics
Tuesday, July 21, 2009
Genetic background & medicine, HIV & differences between blacks & whites
posted by
Razib @ 7/21/2009 01:24:00 PM
The Duffy-null state is associated with a survival advantage in leukopenic HIV-infected persons of African ancestry:
Persons of African ancestry, on average, have lower white blood cell (WBC) counts than those of European descent (ethnic leukopenia), but whether this impacts negatively on HIV-1 disease course remains unknown. Here, in a large natural history cohort of HIV-infected subjects we show that although leukopenia...was associated with an accelerated HIV disease course, this effect was more prominent in leukopenic subjects of European than African ancestry. The African-specific -46C/C genotype of Duffy Antigen Receptor for Chemokines (DARC) confers the malaria-resisting, Duffy-null phenotype, and we found that the recently described association of this genotype with ethnic leukopenia extends to HIV-infected African Americans (AA). The association of Duffy-null status with HIV disease course differed according to WBC but not CD4+ T cell counts, such that leukopenic but not non-leukopenic HIV+ AAs with DARC -46C/C had a survival advantage compared with all Duffy-positive subjects. This survival advantage became increasingly pronounced in those with progressively lower WBC counts. These data highlight that the interaction between DARC genotype and the cellular milieu defined by WBC counts may influence HIV disease course, and this may provide a partial explanation of why ethnic leukopenia remains benign in HIV-infected African Americans, despite immunodeficiency. Duffy status is a highly ancestrally informative trait. This is a case where the relatively low between population variance found among humans does not apply. Rather, it seems that the Duffy null phenotype is a recent adaptation to malaria among West Africans. Because malaria has such a strong fitness implication many independent genetic adaptations have emerged, many of them with other negative side effects. On net individuals with side effects may still have higher fitness in an environment where malaria is endemic. Sometimes the net benefit is most evidence on a population wide scale, sickle-cell anemia is a deleterious homozygote which exists because of the much higher frequency of heteryzogytes vis-a-vis wild type homozygotes. Many malaria adaptations exhibit the large effect dynamic and suboptimal characteristic which one might except from the early stages of natural selection in a Fisherian model. You deal with the adaptive pressures of the present and let the future take care of itself. In this case, the future involved HIV: The researchers found that leukopenia was generally associated with a faster disease progression from HIV to AIDS, independent of known predictors of AIDS development. "On average, leukopenic European Americans progressed nearly three times faster than their non-leukopenic African or European counterparts," explained Hemant Kulkarni, MD, first author of this study. "However, leukopenic African Americans had a slower disease course than leukopenic European Americans, even though twice as many African Americans in the study had leukopenia." There are no doubt details in the genetic architecture of those with the null genotype worth future investigation. Labels: Genetics, human biodiversity, Population genetics, race
Monday, June 08, 2009
Genetic Architecture of Tameness in a Rat Model of Animal Domestication:
A common feature of domestic animals is tameness-i.e., they tolerate and are unafraid of human presence and handling. To gain insight into the genetic basis of tameness and aggression, we studied an intercross between two lines of rats (Rattus norvegicus) selected over >60 generations for increased tameness and increased aggression against humans, respectively. We measured 45 traits, including tameness and aggression, anxiety-related traits, organ weights, and levels of serum components in >700 rats from an intercross population. Using 201 genetic markers, we identified two significant quantitative trait loci (QTL) for tameness. These loci overlap with QTL for adrenal gland weight and for anxiety-related traits and are part of a five-locus epistatic network influencing tameness. An additional QTL influences the occurrence of white coat spots, but shows no significant effect on tameness. The loci described here are important starting points for finding the genes that cause tameness in these rats and potentially in domestic animals in general. Also see ScienceDaily. Labels: Genetics, Population genetics
Friday, June 05, 2009
 Iceland has long been of some interest because of its peculiar demographic history and their genetic consequences. So a new paper in PLoS Genetics is of interest, The Impact of Divergence Time on the Nature of Population Structure: An Example from Iceland: Iceland has long been of some interest because of its peculiar demographic history and their genetic consequences. So a new paper in PLoS Genetics is of interest, The Impact of Divergence Time on the Nature of Population Structure: An Example from Iceland:The Icelandic population has been sampled in many disease association studies, providing a strong motivation to understand the structure of this population and its ramifications for disease gene mapping. Previous work using 40 microsatellites showed that the Icelandic population is relatively homogeneous, but exhibits subtle population structure that can bias disease association statistics. Here, we show that regional geographic ancestries of individuals from Iceland can be distinguished using 292,289 autosomal single-nucleotide polymorphisms (SNPs). We further show that subpopulation differences are due to genetic drift since the settlement of Iceland 1100 years ago, and not to varying contributions from different ancestral populations. A consequence of the recent origin of Icelandic population structure is that allele frequency differences follow a null distribution devoid of outliers, so that the risk of false positive associations due to stratification is minimal. Our results highlight an important distinction between population differences attributable to recent drift and those arising from more ancient divergence, which has implications both for association studies and for efforts to detect natural selection using population differentiation. Figure 3 is a PCA map which shows how individuals from different regions of Iceland sort out. The Scottish and Norwegian populations are there two, and they don't vary much along the components of variation which Icelanders sort out along, the conclusion being that the Iceland variation isn't due to different ancestral proportions. They further calculate that if the ancestral Iceland populations were like the modern Scottish and Norwegian ones, Icelanders are ~35% Scottish and ~65% Norwegian. Most of the differences between Icelanders and continental Europeans is no doubt due to drift because of their very small population size, no migration due to their isolation and the a few specific bottleneck events. But a section on natural selection in Icelanders is interesting: We found eight SNPs, representing two chromosomal regions, for which the evidence of unusual population differentiation was genomewide-significant...Six of the SNPs lie in or near the TLR (toll-like receptor) genes TLR10 and TLR1, while the other two lie inside the NADSYN1 (NAD synthesase 1) gene.... Toll-like receptors were pinpointed in a recent paper as likely possibilities for localized adaptation. Labels: Genetics, Population genetics
Tuesday, June 02, 2009
In light of p-ter's post on KITLG and cancer risk, I stumbled onto this today, Earwax, osmidrosis, and breast cancer: why does one SNP (538G>A) in the human ABC transporter ABCC11 gene determine earwax type?:
One single-nucleotide polymorphism (SNP), 538G>A (Gly180Arg), in the ABCC11 gene determines the type of earwax. The G/G and G/A genotypes correspond to the wet type of earwax, whereas A/A corresponds to the dry type. Wide ethnic differences exist in the frequencies of those alleles, reflecting global migratory waves of the ancestors of humankind. We herein provide the evidence that this genetic polymorphism has an effect on the N-linked glycosylation of ABCC11, intracellular sorting, and proteasomal degradation of the variant protein. Immunohistochemical studies with cerumen gland-containing tissue specimens revealed that the ABCC11 WT protein was localized in intracellular granules and large vacuoles, as well as at the luminal membrane of secretory cells in the cerumen gland, whereas granular or vacuolar localization was not detected for the SNP (Arg180) variant. This SNP variant lacking N-linked glycosylation is recognized as a misfolded protein in the endoplasmic reticulum and readily undergoes ubiquitination and proteasomal degradation, which determines the dry type of earwax as a mendelian trait with a recessive phenotype. For rapid genetic diagnosis of axillary osmidrosis and potential risk of breast cancer, we developed specific primers for the SmartAmp method that enabled us to clinically genotype the ABCC11 gene within 30 min I blogged a paper on this SNP relating it to earwax form a few years ago. Also see ScienceDaily. The variation in earwax seems to conform pretty closely to that of EDAR. Labels: Genetics, Population genetics
Monday, May 11, 2009
Analysis of genomic diversity in Mexican Mestizo populations to develop genomic medicine in Mexico. The title says it all, so I won't post the abstract. The article is OA, so you can read the whole thing, but I thought this figure from the supplements was pretty informative:
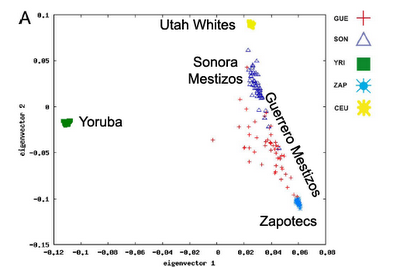 Sonora is exactly where you would expect Mestizos to be the most European, while Guerrero on the coast has more African ancestry. See the paper for other Mexican provinces. The use of a Northwest European population is of course somewhat imperfect as the white ancestry of Mestizos is Iberian (though European populations really are not very differentiated in the worldwide context). Additionally, the Zapotecs would be imperfect representative of the genetic variation of all the Amerindians of Mexico (some of whom are likely to emigrated from the American Southwest relatively recently). Sonora is exactly where you would expect Mestizos to be the most European, while Guerrero on the coast has more African ancestry. See the paper for other Mexican provinces. The use of a Northwest European population is of course somewhat imperfect as the white ancestry of Mestizos is Iberian (though European populations really are not very differentiated in the worldwide context). Additionally, the Zapotecs would be imperfect representative of the genetic variation of all the Amerindians of Mexico (some of whom are likely to emigrated from the American Southwest relatively recently).Labels: Genetics, Population genetics
Monday, April 27, 2009
The New York Times has an interesting little piece on bones, including a description of the unsettling genetic disorder fibrodysplasia ossificans progressiva:
When Harry Eastlack was 5 years old, he broke his left leg while out playing with his sister. The fracture failed to set properly, and soon his hip and knee had stiffened up as well. Examining the boy, doctors found ominous bony growths on the muscles of his thigh. Within a few years, bony deposits had spread throughout Harry's body, infiltrating his chest, neck, back and buttocks. Surgeons tried to cut the excess bone away, only to watch it grow back thicker and more invasive than before.Fun fact: the gene that causes this disease is ACVR1, which lies in a region of extended haplotype homozygosity and extreme population differentiation suggestive of recent positive selection in non-African populations. Labels: Genetics, Population genetics
Wednesday, April 15, 2009
Genetic markers and population history: Finland revisited:
The Finnish population in Northern Europe has been a target of extensive genetic studies during the last decades. The population is considered as a homogeneous isolate, well suited for gene mapping studies because of its reduced diversity and homogeneity. However, several studies have shown substantial differences between the eastern and western parts of the country, especially in the male-mediated Y chromosome. This divergence is evident in non-neutral genetic variation also and it is usually explained to stem from founder effects occurring in the settlement of eastern Finland as late as in the 16th century. Here, we have reassessed this population historical scenario using Y-chromosomal, mitochondrial and autosomal markers and geographical sampling covering entire Finland. The obtained results suggest substantial Scandinavian gene flow into south-western, but not into the eastern, Finland. Male-biased Scandinavian gene flow into the south-western parts of the country would plausibly explain the large inter-regional differences observed in the Y-chromosome, and the relative homogeneity in the mitochondrial and autosomal data. On the basis of these results, we suggest that the expression of 'Finnish Disease Heritage' illnesses, more common in the eastern/north-eastern Finland, stems from long-term drift, rather than from relatively recent founder effects. The Wikipedia entry on Swedish-speaking Finns highlights the controversies about their origins. Some claim that they are Finns who switched to Swedish as they rose up the class hierarchy, while the alternative model is that they are the descendants of immigrants who arrived after the Swedish conquest of much of Finland during the 12th and 13th century. Additionally, there is the countervailing dynamic whereby it seems that many Swedish speaking Finns have been assimilated into the Finnish speaking population since the 19th century. Of course it doesn't need to be a black-white dichotomy of immigrants vs. the indigenous. But the genetic data can help quantify the proportion of gene flow due to migration vs. acculturation. Right now the genetic data don't seem to support a strong version of the hypothesis that Swedish-speaking residents of Finland are simply the descendants of those who switched to the Swedish language. Rather, a non-trivial level of migration seems likely to have been an integral part of the process. H/T Dienekes Related: The genetics of Fenno-Scandinavia, Finns as European genetic outliers and Estonians are not like Finns. Labels: Finn baiting, Population genetics
Thursday, April 09, 2009
There was some talk about Pygmies on the post about Jerry Coyne's weblog. PLoS Genetics has a new paper up on the topic of Pygmy origins and their relationship to non-Pygmy populations. I've blogged it over at ScienceBlogs.
Labels: Evolution, Genetics, Population genetics, Pygmies
Tuesday, March 24, 2009
Signals of recent positive selection in a worldwide sample of human populations...again, sort of
posted by
Razib @ 3/24/2009 10:46:00 AM
New paper in Genome Research, Signals of recent positive selection in a worldwide sample of human populations:
Genome-wide scans for recent positive selection in humans have yielded insight into the mechanisms underlying the extensive phenotypic diversity in our species, but have focused on a limited number of populations. Here, we present an analysis of recent selection in a global sample of 53 populations, using genotype data from the Human Genome Diversity-CEPH Panel. We refine the geographic distributions of known selective sweeps, and find extensive overlap between these distributions for populations in the same continental region but limited overlap between populations outside these groupings. We present several examples of previously unrecognized candidate targets of selection, including signals at a number of genes in the NRG-ERBB4 developmental pathway in non-African populations. Analysis of recently identified genes involved in complex diseases suggests that there has been selection on loci involved in susceptibility to type II diabetes. Finally, we search for local adaptation between geographically close populations, and highlight several examples. I've blogged it at ScienceBlogs, and so has Genetic Future, and John Hawks offers a response. Though there are so many references to the Supplements, which aren't online, I feel like there's on more course remaining.... Labels: Genetics, Population genetics
Saturday, February 14, 2009
From genome-wide data to insights into human population structure
posted by
p-ter @ 2/14/2009 12:28:00 PM
The most important public sources of genetic data for understanding human population genetics to date have come from the HapMap and the Human Genome Diversity Panel. A new paper presents an analysis of human population structure in a somewhat complementary data set assembled from thousands of samples largely from Mexico, Europe, East Asia, and Central Asia (the European population in this data were previously examined in great detail). A couple highlights:
1. I recently mentioned a pair of papers that presented conflicting results about the relative effective population sizes of the X chromosome and the autosomes. In this paper, the authors write: Interestingly, we observed a significantly higher degree of divergence in allele frequency across X chromosome SNPs where we estimate FST to be 9.7%. This value is about 40% higher than the expected value of 6.8% derived from a many-deme island model and accounting for the 4:3 ratio of autosomes to sex chromosome. The higher degree of population divergence at X chromosome SNPs suggests a smaller effective population size of the X than that predicted from Mendelian genetics.This is additional evidence that the observation that needs to be explained is a lower Ne on the X chromosomes as compared to the autosomes, rather than the reverse. 2. Within Europe, the authors find that, in general, haplotype diversity decreases from the south to the north, an observation consistent with expansion from the Middle East into Europe via a series of serial bottlenecks. However, there is high haplotype diversity in Southwestern Europe, which is inconsistent with such a simple model. The authors show that many of the SW European haplotypes match up with those in Africa, suggesting recent migration directly from Africa across the Mediterranean could partially explain this phenomenon. I may have more to say once the Supplementary Information are available online, but this is a nice example of leveraging samples collected for medical genetics studies around the world for further understanding in population genetics. Labels: Population genetics
Saturday, January 10, 2009
Selection or demography in differences between human populations?
posted by
p-ter @ 1/10/2009 08:13:00 AM
Dan MacArthur points to a paper claiming that large allele frequency differences between populations are due to demographic effects. The data the authors are working with is a set of a few thousand markers (SNPs and others) genotyped on 53 populations from across the world. Their main points boil down to two things:
1. "Large" allele frequency differences are "surprisingly" common between human populations. 2. Such allele frequency differences are not enriched near genes (as would be expected if genes are more likely targets of positive selection than non-genic regions). This work can essentially be seen as a push back against the trend towards finding "evidence" of positive selection in the human genome in any gene one finds interesting, and the authors cite a number of papers that fully or partially base their claims for selection on allele frequency differences between populations. As a warning about the caveats in such types of analysis, this is a useful paper, but it's important not to overstate what the data actually say: 1. When the authors say that large allele frequency differences are common, it's important to define "large". In this case, they're talking about things with an allele frequency difference of 0.3 or above. That is, if an allele is at 30% frequency in Africa and 60% frequency in Asia, that counts. How you define large is obviously subjective, and personally I wouldn't have chosen that threshold. But in any case, the authors are right to say that if you see an allele frequency difference of 0.3 and 0.4 between continental populations in your favorite gene, that alone is not strong evidence for selection. 2. The enrichment (or lack thereof) of large allele differences near genes was more comprehensively studied in a paper from about a year ago. The authors there found that there is indeed such an enrichment, but that it occurs at a more stringent definition of "large" than the one considered here. So the fact that allele frequency differences of 0.3 are not enriched near genes is not all that surprising. To summarize, this paper shows that many claims about selection on individual loci based entirely on modest (what the authors call large) allele frequency differences between populations are massively overstating their evidence. But then again, you already knew that. Labels: Population genetics
Sunday, December 21, 2008
The X chromosome in humans is something of an exception with regards to the rest of the genome--as it's diploid only in females, the population genetic forces on it are slightly different. In particular, the effective population size of loci on the X, in a standard neutral model, is 3/4 that of the autosomes. In different demographic models, this fraction can change, so comparing the X to the autosomes is potentially an important tool for understanding human demography.
In a paper published earlier this year, Hammer et al. analysed a data set they had collected of sequences at 40 loci (20 autosomal and 20 on the X) in a number of populations. They saw a striking pattern (the relevant figure from their paper is on the right): in every population they looked at, their estimate of the ratio of effective population sizes on the X and autosomes was greater than 0.75. After additional analyses, they interpreted this as the signature of polygamy in human history. At the same time, another group (Keinan et al.) was independently looking at this issue in other datasets. Their analysis, published today is markedly different. In particular, they see the exact opposite of the pattern in Hammer et al.--a decrease in the X/autosome ratio in effective population size compared to 0.75 (a figure from their paper is on the right. Note that the y-axis is the same in both this and the Hammer et al. figure--the x/autosome ratio in Ne. In both, the solid horizontal line is at 0.75).  . And this is not due to extremely different methodologies--one of the analyses presented by Keinan et al. is very similar to that in Hammer et al., only using different data. . And this is not due to extremely different methodologies--one of the analyses presented by Keinan et al. is very similar to that in Hammer et al., only using different data.So this is all a bit odd, to say the least. Labels: Population genetics
Saturday, December 06, 2008
Check out the the charts over at Steve Hsu's site. The author of a forthcoming paper sent him a draft. Since around 2/3 of the population of East Asia resides in China, there would be some value-add in getting many disparate samples from Han groups from all over the country and seeing what the population structure in the nation itself is.
Update: Here's the paper. They do in fact look at geographic structure in China, but it is at a relatively coarse level. Below the fold is a figure which I've reedited a bit for more illustrative power. The plot is across the first two principal components. Unfortunately many of these groups (e.g., Miao, who Americans know as┬ĀHmong) are obscure to most, though I'm sure the Xibo's in the readership wil appreciate my labels. Also, remember that a majority of Chinese Americans are from southern dialect groups and regions. The oldest communities are Cantonese, but most of the recent immigrants are from Fujian, and the Taiwanese are over 90% of Fujian origins themselves (the residual being from all over China due to the post-1949 infux).  Labels: Population genetics
Thursday, November 27, 2008
From time to time I give links to those of my old posts that may still be worth reading. Previous guides are here: 1, 2, 3, 4.
It is over two years since the last update. In that time most of my posts have been on the history of population genetics, and especially on the 'founding fathers', R. A. Fisher, J. B. S. Haldane, and Sewall Wright. I recently finished a long series of Notes on Sewall Wright, so this is a convenient time to take stock. Most of these posts are long, and aimed not so much at day-to-day readers as at people searching for specific topics. Notes on Sewall Wright On Reading Wright gave an overview of the planned series of notes, and includes some general reflections on Wright's reputation. Before continuing with the series as planned, I realised that I needed to cover an additional topic, Wright's Method of Path Analysis This note is especially concerned to clarify the concept of a path coefficient, and the relationship between Wright's method and multiple regression. In preparing the note on path analysis, I wanted to refer to some source containing the material on the statistical theory of correlation and regression that would be needed to understand Wright's work. I could not find a suitable source, so I decided to write it myself, using notes I have made on the subject over the years. Notes on Correlation, Part 1 covers the general concepts of correlation and regression, and the justification for using them (which, like much in the foundations of statistics, is a moot point). Part 2 proves some key theorems on the correlation and regression of two variables, and discusses problems of interpretation. Part 3 outlines the theory of correlation and regression for more than two variables. This is particularly important for the understanding of Wright's path analysis. After the note on Path Analysis I got back on the series as planned, with the following notes. The measurement of kinship tries to explain Wright's approach to this, by contrasting it with the now more familiar methods of Gustave Malecot. The essential point is that Wright's kinship coefficients are in principle correlation coefficients rather than probabilities of identity (as in Malecot's system). A consequence of this is that kinship (or relatedness, or inbreeding) is relative to a specified population. The kinship between randomly selected individuals within such a population, relative to that population, is on average zero. This has implications for Hamiltonian inclusive fitness. Another implication is that Wright's kinship coefficients can be, and often are, negative (unlike Malecot's probabilities). Wright's F-statistics. Wright devised a series of statistics known as F-statistics for measuring relationship and diversity within or between populations. The best known of these is FST, which is widely used as a measure of the genetic divergence between sub-populations of a species. My note traces the evolution of the F-statistics in Wright's work. Genetic drift.. This note was originally going to be called 'Inbreeding and the decline of genetic variance', but that is not a very catchy title. I try to clarify the connection between genetic drift, inbreeding, and the decline of heterozygosis (a measure of genetic diversity). The note includes a detailed commentary on Wright's proof that heterozygosis tends to decline by 1/2N per generation. Population size. I discuss the concept of effective population size and point out that Wright overlooked an important class of cases where effective population size is much larger than the current number of breeding adults. Migration. Migration is important to Wright's theories because even very low rates of migration suffice to prevent subpopulations of a species diverging by genetic drift. The note traces Wright's work on the subject including his famous article on 'Isolation by distance'. The adaptive landscape. Wright is closely associated with the concept of the adaptive landscape, though as far as I can find Wright himself never used this term. My note especially aims to explain the concept of a selective peak, and why Wright believed that there are a multitude of distinct selective peaks, usually of different fitness. In a related post on the Adaptive Landscape: Miscellaneous points, I discussed some issues not directly concerned with Wright, such as Stuart Kauffman's NK model, the relationship between selective peaks for genotypes and for gene frequencies, and the accessibility and stability of peaks. The shifting balance theory of evolution. This final note in the series is split into two parts. Part 1 examines the origins of Wright's famous shifting balance theory, and analyses the contents of the original version of the theory, as published in 1929-31. Part 2 explores subsequent developments in the theory, some of which are very important. Notably, as early as 1932 Wright abandoned his insistence that only genetic drift in small populations could take a population away from a suboptimal selective peak, as he now accepted that environmental fluctuations could have the same effect. In my view this removed much of the rationale for Wright's emphasis on population structure in evolution, though Wright himself never fully absorbed the implications of the change, which many biologists have overlooked. Altogether, this series of posts would come to over 100 print pages. That's very nearly a book's worth! Alas, even if there were a market for such a boring book, I don't have the time, energy, or expertise to research and write it to the necessary standards, but I hope that anyone making a serious study of Wright will find something useful in my posts. R. A. Fisher My various notes on R. A. Fisher are mainly attempts to correct misunderstandings of his views which I have come across from time to time. Fisher and Wright on population size (and here). These two notes were written shortly before I started my series of notes on Sewall Wright. Fisher is sometimes thought to have believed that entire species are randomly mating single populations. As this is palpably false, it is worth examining what Fisher really thought. In my first note I show, using Fisher's publications and letters, that he believed that migration between districts was usually frequent enough to offset their divergence by genetic drift. This does not imply that species are literally random mating (if they were, migration would be irrelevant), but only that for many purposes they can be treated as if they were. In the second note I examine what Fisher says about the actual population size of species. An Addendum is here. Fisher on epistasis. It is sometimes claimed that Fisher ignored epistatic gene effects or considered them unimportant. My post shows that Fisher took account of epistasis in a variety of ways. Two further posts produce additional evidence: here and here. Fisher on the adaptive landscape Following my note on Sewall Wright's adaptive landscape concept, I wrote this post on Fisher's views on the subject. Notably, he believed that environmental change, particularly in the biotic environment, made the idea of a constant landscape inapplicable. Fisher on inclusive fitness In this short post I draw attention to a passage by Fisher which contains a general anticipation of Hamilton's concept of inclusive fitness. J. B. S. Haldane I have written much less about Haldane than about Fisher and Wright. This is not because Haldane was less important or original. Haldane probably originated more of the basic results of population genetics than either of the others. But I tend to write posts mainly on issues that are obscure or controversial, whereas most of Haldane's results are clear and uncontroversial. I have however devoted two posts to Haldane: one on Haldane's Dilemma, which examines Haldane's pioneering attempt to quantify the amount of genetic change possible by natural selection in a given period (see here for some corrections), and Haldane's Selection Theorem which comments on Haldane's proof that the probability that an individual favourable mutation will be successful is 2s, where s is the coefficient of selection. Odds and ends Finally, a few posts cover other issues. Good Point? arises from a study by the economists Samuel Preston and Cameron Campbell. If intelligence is partly inherited, and less intelligent people on average have more children, it seems to follow that the average intelligence of the population will decline from one generation to the next. Preston and Campbell use an elaborate mathematical model to show that this is not necessarily the case. My post examines the argument, using a much simpler model due to the statistician I. J. Good. Briefly, I conclude that the argument is mathematically possible but biologically unrealistic. The case illustrates the danger of using sophisticated mathematics without properly considering the underlying assumptions. Heterosis and the Flynn Effect looked sceptically at claims that heterosis (reduced inbreeding) might explain the long term increase in IQ scores. Origins of the British is a piece examining the evidence on the ethnic origins of the people of the British Isles, following the recent book by Stephen Oppenheimer. Group Selection and the Wrinkly Spreader takes a look at a recent defence of group selection by E. O. and D. S. Wilson, by examining in detail an example (the 'wrinkly spreader' variant of a certain bacterium) that they claim is a good case of group selection in action. It isn't. Ethnic Genetic Interests Revisited looks at the new edition of Frank Salter's book Ethnic Genetic Interests, which includes comments on my own critique of the first edition. Genophilia traces the origins of the term 'genophilia', which has been wrongly attributed to Francis Galton. Labels: Burbridge, Population genetics
Sunday, November 23, 2008
I recently posted a note on an anticipation of Hamilton's concept of inclusive fitness by R. A. Fisher in the Genetical Theory of Natural Selection.
As I pointed out, in that passage Fisher did not quantify the effect of what he called 'indirect effects of natural selection', so he did not state what we now call 'Hamilton's Rule' (though later in GTNS he came close to it in his discussion of distasteful insects). However, I have noticed the following passage in a letter from Fisher to Leonard Darwin dated 27 June 1929, which states Hamilton's Rule for the special case of parental care: The reproductive value at different ages must determine the extent to which parental care pays. If all ages were of equal reproductive value, a species would tend to benefit its offspring up to the point at which the offspring gains double the advantage which the parent loses, but no further. Of course immature offspring are usually worth much less, and so should be cared for only at a cheaper rate still. But if crocodiles were able to recognise their mature offspring, I suppose they would co-operate with them not only on terms of mutual advantage, but on terms of joint advantage so long as the loss of either did not exceed half the gain of the other. Hence society starts with the family. - Natural Selection, Heredity and Eugenics: Including selected correspondence of R. A. Fisher with Leonard Darwin and others, edited by J. H. Bennett (1983), p.104-5 The important qualification about the maturity of the offspring is probably also in Hamilton somewhere, but I can't immediately find it. Dawkins makes a similar point in his '12 Misunderstandings of Kin Selection'. Added: I had another skim through Hamilton's papers, but I still couldn't find a discussion of the maturity point. However, I imagine Hamilton would have said that differences of maturity should be taken into account in quantifying the 'benefit' to an offspring of a given amount of parental care. So, for example, in a species with very high infant mortality, the benefit of a given amount of resources to an immature offspring, measured by the expected number of its own future offspring, would be less (other things being equal) than to an offspring who has already reached sexual maturity. Against this, 'other things' are seldom equal, and the benefit of a given amount of resources (e.g. food) to a newborn may be much greater than to an older offspring which can already fend for itself. Labels: Burbridge, Population genetics
Monday, November 10, 2008
Do you have some marginal time today? Well, now you really don't, play around with the HGDP browser. If you click and find yourself a bit bewildered, read Do It Yourself: searching for evolution's signature in 53 human populations over at Genetic Future.
Related: So you want to be a population geneticist. Labels: Population genetics
Sunday, November 09, 2008
Notes on Sewall Wright: The Shifting Balance Theory (Part 2)
posted by
DavidB @ 11/09/2008 01:32:00 AM
Part 1 of this note dealt with Sewall Wright's Shifting Balance theory of evolution (the SBT) in its original form, as propounded between 1929 and 1931. This final part deals with subsequent developments in the theory. These include refinements and elaborations, some changes of emphasis, one major addition, and one major change of substance. In particular I will cover:http://www.blogger.com/post-edit.g?blogID=10083047&postID=4815748383060203879
Blogger: Gene Expression - Edit Post "Notes on Sewall Wright: The Shifting Balance Theo..." 1. The role of new mutations 2. The concept of selective peaks 3. The effect of changes in environment 4. The adaptiveness of evolution 5. The process of intergroup selection 6. The three phases of the shifting balance. I will throw in a few remarks about Fisher and Haldane as well. NB: all page references are to Evolution: Selected Papers unless otherwise stated. Spelling and punctuation of quotations are as printed (some use American and some use British spelling). Square brackets indicate comments of my own. 1. The role of new mutations First, a few words are necessary about the meaning of 'mutation'. In the 1930s very little was known about the physical and chemical nature of genes and therefore about the nature of changes to genes, in other words 'mutations'. In 1939 Wright gave a useful statement of current assumptions at that time: 'Presumably any particular gene can arise at a single step from only certain of the others and in turn mutate only to certain ones but the latter may be capable of producing mutations which could not have arisen from the former at one step and so on through a branching network of potentially unlimited extent' (306). This implies a 'step-by-step' evolution of genes themselves. Each gene may be said to have a first appearance in time, though recurrence of the same gene at different times is not excluded. The occurrence of mutations depends on the prior existence of the genes of which they are variants, so a particular type of mutation itself has an origin in time. The opportunity for mutations of a particular type will also depend on the frequency of the relevant genes in the population. If a gene is changing in frequency, the opportunity for new mutations of that gene will also be changing. We may therefore expect the rate of specific mutations to increase or decrease over time. This may explain some otherwise obscure comments in Fisher's Genetical Theory of Natural Selection (GTNS). In several places Fisher assumes that any new mutation will initially have a low rate of occurrence, but that this rate will increase over time (see especially GTNS p.78). This assumption makes sense if Fisher held the same view as Wright on the nature of mutations. Wright's original formulation of the SBT said little about the role of beneficial new mutations in evolution. In 'Evolution in Mendelian populations' (EMP) (1931) Wright said only that in very large populations 'there is little scope for evolution. There would be complete equilibrium under uniform conditions if the number of allelomorphs at each locus were limited. With an unlimited chain of possible gene transformations, new favorable mutations should arise from time to time and gradually displace the hitherto more favored genes but with the most extreme slowness even in terms of geologic time' (150). This negative assessment of the prospects for evolution in large undivided populations conflicted with that of Fisher in GTNS, which appeared in 1930 after Wright's 'Evolution in Mendelian populations' (EMP) (1931) had been sent for printing. (A few short notes were added to take account of Fisher's work, but major changes were not possible.) Whereas Wright had concluded that large freely interbreeding populations were unfavourable to progressive evolution, Fisher believed that large populations (without strong barriers to gene flow) were favourable to evolution because of the greater scope they offered to new mutations. Fisher reinforced this in his published review of EMP, saying that 'even under static conditions, unless it is postulated that the organism is as well adapted as it could possibly be (in which case, obviously, evolutionary improvement is impossible), the equilibrium will be broken by the occurrence of any favourable mutation, of which a steady stream will doubtless occur in one or other of the very numerous individuals produced in each generation. The advantage of the large populations in picking up mutations of excessively low mutation rate seems to be overlooked [by Wright]... ' (Natural Selection, Heredity and Eugenics, p.288). Here, then, we find one of the major differences in the evolutionary theories of Wright and Fisher. Wright elaborated and defended his position on this issue on several occasions, beginning with his own review of Fisher's GTNS in 1930. He notes that Fisher's 'scheme appears to depend on an inexhaustible flow of new favorable mutations. Dr. Fisher does not go into this matter of inexhaustibility but presumably it may be obtained by supposing that each locus is capable of an indefinitely extended series of multiple allelomorphs, each new gene becoming a potential source of genes which could not have appeared previously. The greatest difficulty seems to be in the posited favorable character of the mutations. Dr. Fisher, elsewhere presents cogent reasons as to why the great majority of all mutations should be deleterious. He shows that all mutations affecting a metrical character 'unless they possess countervailing advantages in other respects will be initially disadvantageous' [see Note 1]. He shows that in any case the greater the effect, the less the chance of being adaptive. [See Note 2] Add to this the point that mutations as a rule probably have multiple effects, and that the sign of the net selection pressure is determined by the greater effects, and it will be seen that the chances of occurrence of new mutations advantageous from the first are small indeed' (85). There is a risk of ambiguity in this conclusion. If Wright means to say that only a small proportion of new mutations will be initially advantageous, his arguments are plausible, though not conclusive. If on the other hand he means to say that the 'chances of occurrence' of any such mutations, even in a large population, are small, the arguments are quite insufficient. It would be like confusing the probability that John Smith will die tomorrow, which is small, with the probability that someone will die tomorrow, which in a large population is virtually certain. Suppose that in a population of one billion, one in 100,000 individuals in each generation show some new mutation or other. There would then be 10,000 such new mutations in the population in each generation. Evidently, even if only a very small proportion of these mutations are advantageous, there might still be (in Fisher's terms) a 'steady stream' of them. Whether or not this is the case is an empirical matter. Wright made similarly negative comments about new mutations on various occasions when defending the SBT: 1932: [under constant conditions] 'further evolution can only occur by the appearance of wholly new (instead of recurrent) mutations, and ones which happen to be favorable from the first. [Comment: this is valid only if 'new' means 'new under the same conditions'. Evolution might also occur through recurrence of mutations previously unfavourable but now favourable under new conditions.] Such mutations would change the character of the field [the 'adaptive landscape'] itself, increasing the elevation of the peak occupied by the species. Evolutionary progress through this mechanism is excessively slow since the chance of occurrence of such mutations is very small [comment: note the same ambiguity as in Wright's review of GTNS] and, after occurrence, the time required for attainment of sufficient frequency to be subject to selection to an appreciable extent is enormous' 165). [The last remark is puzzling. Any favourable new mutation is subject to selection from the outset, but it is at risk of being lost by random drift before it becomes safely established. It is not 'safe' until it has recurred a few hundred times. But in a large population, even with very low mutation rates this should only take a few hundred generations, which is not long in evolutionary time. This is one of Fisher's main arguments for the evolutionary advantage of large population size: see GTNS p.78. Once a mutation has reached a level of a hundred or so copies - say, a frequency of 1 in 10,000,000 in a population of a billion - the rate of advance will depend on the selective advantage of the gene. If the selective advantage is such as to double its frequency in 1,000 generations - equivalent to an advantage of rather less than 1 in 1,000 - the gene will go from first appearance to fixation (or equilibrium against back-mutation) in less than 30,000 generations. [See Note 3] This is not very long in geological time, though it would be imperceptibly slow to human observers, and until the later stages the gene would still be rare.] 1939: 'there is very little chance of occurrence of wholly new alleles in a large freely interbreeding population. There is also very little chance that any new mutation will be favorable at its first occurrence and even if favorable very little chance that it will attain sufficient frequency to be subject to selection to an appreciable extent' (321) [The italics for 'large' are Wright's own. The implicit assumption seems to be that in a large population every good mutation will already have been found. But note my previous comment that the advantageousness of a mutation is relative to conditions.] 1948: 'Presumably all mutations that are likely to arise at one or two steps from the more abundant genes present in the population have been tried by natural selection and found wanting, and thus are found at negligibly low frequencies if at all. There may be very valuable mutations which could only arise through a succession of unfavourable ones but these will have very little chance of occurring' (535) [see the previous comments] 1959: 'A genetic system can take the step from one selective peak to another one only by some non-selective process. A novel mutation may do this by creating a new peak, but this must be an excessively rare event' (Tax, p.451) Wright maintained his opposition to the importance of new mutations to the end of his career. But his arguments are always brief and unquantified. There is a recurring ambiguity, as noted above, between the probability that a given new mutation will be advantageous, and the probability that any advantageous new mutation will occur. Fisher's view (GTNS p.78), was that in large populations, of the order of a billion (which includes most plant and invertebrate animal species), such mutations would occur often enough to be important in evolution. Wright opposed this conclusion, but it is difficult to avoid the feeling that in doing so he was trying to shore up a position which he had adopted without first considering mutation. It should at once be said that Fisher was equally stubborn (and more intemperate) in defending his own positions. 2. The concept of selective peaks As noted in my post on Wright and the adaptive landscape, in 1932 Wright introduced the metaphor of a multidimensional field of gene combinations. I have discussed Wright's adaptive landscapes at length (see also here), so I will not repeat those discussions now. The point I wish to emphasize here is that the concept of selective peaks, valleys, etc, as introduced in 1932 was not just a new metaphor adopted for purposes of exposition, but an important addition of substance to the SBT. From 1932 onwards it is a fundamental part of the SBT that there is a multiplicity of selective peaks in the field of possibilities available to a population. Many of these peaks are of different height (fitness). Under the influence of selection alone, and under constant conditions, a population cannot move from one peak to another. Under selection a population will tend to move towards one of the peaks, but usually the closest, which will seldom be the highest. It is therefore very likely that a population will be 'trapped' on an inferior peak, from which it cannot move purely by selection under constant conditions. This aspect of the SBT is so important, and so familiar from Wright's later writings, that it is tempting to assume that in substance it was already there in the original version of the theory, even if the analogy of 'peaks' and 'valleys' was missing. In purely genetic terms, the meaning of a 'peak' in the landscape is that there is some set of gene frequencies such that any small departure from that set is opposed by selection. If there is more than one such set, there are multiple peaks. But the terminology of 'peaks', etc, is inessential. The substance of the theory could be stated quite well without it. It is therefore natural to expect some such equivalent statement in EMP, but I have not found one. It is true that, when discussing evolution in large populations in his 1929 summary, Wright does say that 'changed conditions cause a usually slight and reversible shift of the gene frequencies to new equilibrium points' (78), but in the context of his discussion in EMP (150) it appears that Wright was thinking only of a shift in the equilibrium between selection and mutation. His repeated claims that such shifts are essentially reversible would be difficult to reconcile with the concept of multiple peaks, and indeed, once Wright had clearly formulated that concept, he abandoned the claim of irreversibility. The concept of multiple selective peaks is closely related to Wright's emphasis on epistatic fitness interactions, but this familiar feature of Wright's philosophy of evolution is also lacking from EMP. The beginnings of a new emphasis on epistasis can be found in 'Statistical theory of evolution' (1931), written after EMP but published slightly earlier. In discussing populations of intermediate size, Wright points out that 'it is the organism as a whole that is selected, not the individual genes, and a gene favored in one combination may be unfavorable in another' (95). And in subdivided populations 'exceptionally favorable combinations of genes may come to predominate in some of the subgroups' (95). But there is still, as far as I can see, no indication that even large populations may have alternative stable states, as proposed by Wright in 1932. It is natural to wonder how Wright arrived at his 1932 conception of multiple selective peaks. It is possible that his reading of the section on 'Simple metrical characters' in GTNS had planted the seed. We know from Wright's correspondence that he was encouraged by receiving an offprint from Haldane in which the latter outlined similar ideas (Provine 275). It is also possible that Wright had privately reached his conception (without the geometrical analogy) much earlier, as Provine seems to think (Provine 275). But if Wright did indeed have the concept in mind when writing the paper which became EMP it is odd that he did not incorporate it in that work. I can only leave this as an unsolved puzzle. 3. The effect of changes in environment As I have mentioned in previous posts (and as is also pointed out by Provine), until 1931 Wright considered that the evolutionary effects of temporary changes in environment would 'usually' or 'essentially' be reversible (78, 85, 150). But in 1932, with his paper on 'The roles of mutation, inbreeding, crossbreeding and selection in evolution', he took a new position. After introducing his concept of the multidimensional field of gene combinations, and the associated diagrams, he notes that 'the environment, living and non-living, of any species is actually in continual change. In terms of our diagram this means that certain of the high places are gradually being depressed and certain of the low places are becoming higher... Here we undoubtedly have an important evolutionary process and one which has been generally recognised. It consists largely of change without advance in adaptation. The mechanism is, however, one which shuffles the species around in the general field. Since the species will be shuffled out of low peaks more easily than high ones, it should gradually find its way to the higher general regions of the field as a whole' (167). This formulation is repeated, usually in similar words, in most of Wright's subsequent general surveys of evolutionary theory, e.g. 323, 374, 535, and 562. It is perhaps not immediately clear (and Wright does not explain) why 'the species will be shuffled out of low peaks more easily than high ones'. Presumably it is partly because higher peaks may have stronger selection coefficients, and will therefore resist drift more strongly, but mainly because, other things being equal, higher peaks will have wider zones of attraction. A population may therefore drift further from the peak but still be pulled back towards it by selection. In geometrical terms, if two solid figures have the same shape, the taller figure will have the larger base. In genetic terms, the higher the fitness of a genotype relative to the average fitness of the population, the wider will be the range of gene frequencies within which the genes making up that genotype will be positively selected. But this is not an absolute rule. If a peak of fitness depends on very specific epistatic interactions of several genes, the peak may be high but narrow, like a spike. In this case a population may be easily jolted out of a high peak by environmental change, and never return to it. Changing environments may therefore be expected to promote mainly genes that are advantageous in a wide range of genetic combinations. We are bound to ask why Wright changed his mind about the effects of environmental change. Wright himself gives no help on this point, because he never (I think) admitted that he had changed his mind. The change in 1932 goes together with Wright's formulation of the adaptive landscape concept, and in one sense goes very naturally with it. If we accept that there are multiple peaks of fitness in the landscape, and that it is largely a matter of chance which peak is most accessible to a population, then any factor which causes populations to move in a quasi-random way around the landscape could have the effect of 'shuffling' the population from one zone of attraction to another. But in another sense there is a tension between the landscape concept and environmental change, since the effect of environmental change is not so much to move the population around a fixed underlying landscape as to modify the landscape itself. As several commentators have suggested, in a changing environment the proper analogy is not so much with a solid landscape as with a choppy sea. It is quite possible that Wright's change of mind in 1932 resulted simply from his own reflection on the issues. But he may also have been influenced by the positions already taken by Fisher and Haldane. As I mentioned in my post on Fisher and epistasis, in the section on 'Simple metrical characters' in GTNS Fisher had pointed out that metrical traits under stabilising selection could lead to multiple stable equilibrium gene frequencies, and that changes in selection coefficients due to environmental change could produce a lasting shift from one equilibrium to another. Wright had certainly read this section of GTNS, since he quotes from it in his review of the book. At that time (1930) he still thought that the effects of environmental change would usually be reversible, but he qualifies that position, saying: 'It may be granted that an irregular sequence of environmental conditions would result occasionally in irreversible changes (because of epistatic relationships), thus giving a real, if very slow, evolutionary process... ' (85). Over the next year Wright may have come to reconsider whether the process would only be 'occasional'. Haldane's The Causes of Evolution (1932, p.56) also contains a highly relevant passage: 'the change from one stable equilibrium to another may take place as the result of the isolation of a small unrepresentative group of the population, a temporary change in the environment which alters the relative viability of different types, or in several other ways...'. Unfortunately I do not know the exact dates of publication of Haldane's book and Wright's article of the same year, so it is not clear whether Wright could have seen it before writing his article. Wright had certainly read an article by Haldane of 1931 on 'Metastable Populations', which also discusses the theory of multiple equilibria, but this article refers only to chance fluctuations in the composition of populations, and not to environmental change, as possible reasons for a switch between alternative equilibria. Whatever the reasons for Wright's new position on environmental fluctuation, he cannot be accused of playing down its importance. Several times he emphasised it: 'here we undoubtedly have an evolutionary process of major importance' (322), 'it can hardly be doubted that this has been one of the most important causes of evolution' (374), and 'there can be no doubt that a large part, perhaps the major portion, of evolutionary change, is of this character' (562). Nevertheless, it has often escaped the notice of later biologists, who assume that Wright continued to see genetic drift as the only way out of evolutionary stagnation. Despite Wright's acceptance of, and even emphasis on, environmental change as a possible cause of 'peak shift', in some respects the implications of this new position were not fully assimilated into Wright's evolutionary philosophy. First, Wright might have been expected to rethink his position on the importance of population size and structure. On the face of it, a population of any size - large, small, or medium - may equally be affected by environmental change, and equally likely to shift from one peak to another. If this is so, Wright's belief in the ineffectiveness of evolution in large populations would need to be reconsidered. I am not aware that Wright did so. Second, if environmental change is capable of upsetting the equilibrium, perhaps other factors might also do so. One such factor is migration. If different gene frequencies are able to evolve in subpopulations, through genetic drift or local selective pressures, then migration between subpopulations may upset the equilibrium in some or all of them. Wright's SBT does allow for one particular effect of migration: if one subpopulation happens to have reached a higher selective peak than others, migration from that subpopulation may shift others towards the higher peak. But my point is that any migration between subpopulations with different gene frequencies may break up the existing equilibria and give the opportunity for new, and often higher, equilibria to be attained. It therefore seems that even if new favourable mutations are too rare, and mutation pressure is too weak, shifts between equilibria might occur in three ways: genetic drift in small subpopulations, environmental changes (biotic or nonbiotic) which might in principle affect populations of any size, and migration between subpopulations of any size. 4. The adaptiveness of evolution I can deal more briefly with this topic because it has been dealt with thoroughly by Provine, who traces the change in emphasis from nonadaptive evolution, even at the level of differences between species, in Wright's early work, to a much stronger emphasis on adaptation in the post-war writings. The only point I would add is that even in his later writings Wright saw adaptation as occurring mainly through intergroup selection. Selection within a single population, large or small, is in Wright's view ineffective in producing continuing adaptation because any single population will soon become stuck on a suboptimal selective peak. Evolution within subpopulations leads to divergence between them, either through genetic drift or fluctuating environmental factors. Neither of these is adaptive with respect to long term trends. This is obvious in the case of genetic drift, but even selection under fluctuating environment may be regarded as a quasi-random factor. It contributes to long-term adaptation only by providing the variation between subpopulations on which intergroup selection can work: 'In this theory [the SBT], the joint effects of random drift and intrademic selection merely supply raw material for interdemic selection' (618). Some subpopulations will, by chance, have combinations of genes which have the potential to increase fitness in the species as a whole, and these are spread by intergroup (interdemic) selection. The processes which generate diversity between subpopulations may be seen as analogous to mutation in the conventional neo-Darwinian framework: each mutation may have some underlying cause, and is not strictly random in the sense that mutations in all directions are equally probable, but it is random with respect to the long-term adaptiveness of the species as a whole. It should be evident by now that Wright's SBT is a radical departure from the neo-Darwinism of Fisher, Haldane, and most other theorists of the 'evolutionary synthesis', and it should not be surprising that it has found admirers among such rebels against the synthesis as the punctuationists and the group selectionists of the last few decades. 5. The process of intergroup selection Despite its importance in the SBT, Wright says little about the process of intergroup (or interdemic) selection. In principle one can envisage three different ways in which groups with higher average fitness could influence the properties of the wider population: a) one group may become extinct, and a fitter group may then expand into the unoccupied territory b) one group may move into the territory occupied by another group and displace it without interbreeding c) members of one group may migrate into the territory of another, and influence its gene pool by interbreeding. I do not think that Wright ever mentions process (a). In various places he seems to favour either process (b) or (c). In 1931 he says that 'exceptionally favorable combinations of genes may come to predominate in some of the sub-groups. These may be expected to expand their range while others dwindle' (95, see also 152). Since there is no mention of interbreeding, this seems to be closest to process (b). In 1932, on the other hand, he says that successful local races 'will expand in numbers and by crossbreeding will pull the whole species toward the new position' (168). This is closer to process (c). In 1939 he combines both (b) and (c), saying successful races 'by cross breeding with other races, as well as by actual displacement of these, will pull the species as a whole toward the new position' (324). In 1940 he says that successful local races may 'tend to displace all other local strains by intergroup selection (excess migration)' (351). The word 'displace' tends to suggest process (b). Also in 1940 he refers to some groups 'supplying more than [their] share of migrants to other regions, thus grading them up to the same type' (375, see also 423). The reference to 'grading up' may seem to imply a mingling of populations and interbreeding (process (c)). There is of course no reason why both processes should not play a part, as explicitly suggested in 1939. But both face some obvious difficulties. With process (b) it is necessary to explain why there is no interbreeding between the different types. This would be surprising unless some degree of reproductive isolation - i.e. speciation - had already evolved. With process (c) the problem is to explain why interbreeding does not break up the advantageous gene combinations on which the superiority of one group is supposed to rest. The problem is expecially severe if the successful group is initially small in relation to the whole population, as assumed at least in the original version of the SBT, with its reliance on genetic drift. This issue has been studied in several recent assessments of the SBT, the general conclusion being that the process is possible but, like the SBT as a whole, requires rather a lot of quantitative conditions to be met if it is to succeed. As I mentioned in Part 1 of this note, 'intergroup selection' as envisaged by Wright has little to do with 'group selection' as envisaged by most of its recent advocates. Wright does not suggest that successful groups have evolved adaptations for group living, or that their members behave 'altruistically' towards each other. His claim is rather that the subdivided population structure allows some groups, by chance, to form combinations of genes that are advantageous to individual fitness. The higher mean fitness of the groups is the resultant of these individual fitness advantages. However, in some of his later writings Wright does mention the possibility of the evolution of altruistic social traits through intergroup selection, for example: 'characters may be fixed [through random drift in small subpopulations] that are favourable to the group as a whole even though disadvantageous in individual competition' (536, see also Tax p.466). The problem, of course, is that this requires migration from other groups to be near zero if the 'altruistic' groups are to survive for more than a brief period without being undermined by freeloaders. 6. The three phases of the shifting balance Finally, in his later writings on the SBT Wright often refers to three 'phases' of the shifting balance. Like the term 'shifting balance' itself, the 3-phase formulation seems to have been first used in the article of 1970 on 'Random drift and the shifting balance theory of evolution'. The phases are described as the 'phase of random drift', in which gene frequencies in each deme drift around the current selective peak; the 'phase of mass selection', in which a deme has drifted into the zone of attraction of a new selective peak, and moves rapidly towards it under the influence of selection; and the 'phase of interdemic selection'. The explicit distinction between three phases seems to be new in 1970, but it is essentially a clarification of the process which had been implicit in various writings at least since 1932. I won't comment further on the substance of the three phases, which have already been discussed under various headings. Conclusions The purpose of this Note has been mainly to analyse the various aspects of the SBT in their chronological development, and not to assess its credibility. A few years ago I drew attention to some recent controversy, mainly in the journal 'Evolution', by biologists pro and con the SBT. These discussions still seem to be relevant, but I note that some aspects of the SBT (or of Wright's philosophy of evolution more generally) have not been sufficiently recognised. One is the important change in 1932 when Wright recognised that environmental fluctuations, as well as genetic drift, could have lasting effects on the genetic equilibrium of a population. Despite Wright repeating this point on several occasions, it has been widely overlooked (Dobzhansky being a notable exception, and Provine a more recent one). There is some excuse for this if, as I have argued, the implications of the change were never sufficiently absorbed by Wright himself. The second point is that Wright was consistently negative towards the prospects for new favourable mutations. I have suggested that his comments involve an ambiguity between the rarity of new favourable mutations among all mutations, which is not disputed, and the rarity of occurrence of any such mutations, even in a large population and over a timescale of many generations. Wright's negative conclusions are only valid if such mutations are rare in both senses. His position implies that the differences between populations, whether closely related species or subpopulations of the same species, will arise mainly by different epistatic combinations of existing genes, rather than by the selection of new variants. This is in principle testable. This is the last of my planned notes on Sewall Wright, and it is a relief to get to the end of the journey. I will not attempt any overall assessment at this stage, but I will probably prepare a post giving links to all the notes in the series, as well as to related notes on Fisher and Haldane. Note 1. See GTNS p.107, but note that according to Fisher, if the effect of the mutation is small (say, no more than 1 percent of the standard deviation of the trait), even mutation rates as low as one in a million may be sufficient to overcome the initial selective disadvantage and eventually push the mutation into a frequency where it is favoured by selection. Note 2. The reference is evidently to the section in GTNS on 'The nature of adaptation'. What Fisher shows, given his assumptions, is that: a) other things being equal, a smaller mutation is always more likely to be advantageous than a larger one. (As Kimura pointed out much later, this is partially offset by the consideration that the size of any advantage is likely to be greater for a larger mutation, and this affects the probability that it will survive in the population. Overall, mutations with effects somewhat above the minimum size have the highest probability of survival.) b) for any given size of mutation, the probability of being advantageous is lower the more aspects of fitness are affected by it. Using a very schematic geometrical model, Fisher quantifies the probability that mutations of a given size will be advantageous. It is assumed in the model that the present position of the organism is at some distance from a local optimum. The probability that a mutation will be advantageous is inversely related both to the size of the mutation and to the square root of the number of dimensions of fitness affected. For very small mutations the probability is close to 1/2, declining to zero for mutations with an effect more than twice the distance between the starting point and the local optimum (this zero probability being an assumption built into the model, rather than proved by it). But note that the probabilities are not always very small, even for mutations with an effect quite substantial relative to the present distance between the organism and the optimum. Also, since the probability declines in proportion only to the square root of the number of dimensions of fitness affected, not to that number itself, the decline is not as rapid as might be feared. Contrary to some popularisations, Fisher does not claim that mutations with very large or complex effects are impossible, or even highly improbable, only that they are less likely to be advantageous than those with smaller and/or simpler effects. Note 3: Some readers may wonder how this can be reconciled with Haldane's rule of thumb that up to one mutation can go to fixation, on average, in every 300 generations - see my post on Haldane's Dilemma. I think the explanation has two parts. First, Haldane's '300 generations' estimate assumes that a gene under selection starts from a position of balance between adverse selection and mutation pressure, and then becomes favourable due to a change in environment. On this assumption the gene will already have a small but not negligible frequency in the population. Second, the '300 generations' figure does not mean that a single gene under selection goes from rarity to fixation in 300 generations, but rather that, on average, one gene could be fixed in every 300 generations. There is a difference between these two claims. Under typical selection intensities of 1 in 1000, or even 1 in 100, the process of fixation for a single initially rare gene would obviously take longer than 300 generations. Haldane's model assumes that there are a number of genes undergoing selection simultaneously or overlapping with each other. If we imagine, say, 100 genes starting the process of selection at the same time, and all taking 30,000 generations to reach fixation, the average number of genes fixed per generation over the period of 30,000 generations would be 100/30,000 = 1/300, but these would all reach fixation in a bunch at the end of the period. More realistically, if the periods of selection are overlapping in a more-or-less random way, and selection has been in progress for long enough, we would expect any period of, say, a thousand generations to see a few genes reaching fixation, with an average of about 1 per 300 generations. References R. A. Fisher, The Genetical Theory of Natural Selection, 1931, variorum edition ed. J. H. Bennett, 1999. R. A. Fisher: Natural Selection, Heredity and Eugenics: Including selected correspondence of R. A. Fisher with Leonard Darwin and others, edited by J. H. Bennett (1983). J. B. S. Haldane, 'Metastable populations', Proceedings of the Cambridge Philosophical Society, 27, 1931, 137-142. J. B. S. Haldane, The Causes of Evolution, 1932 (reprint ed. E. Leigh, 1990) William B. Provine, Sewall Wright and Evolutionary Biology, 1986. Sewall Wright: 'Physiological genetics, ecology of populations, and natural selection', in Evolution After Darwin, vol. 1, ed. Sol Tax, 1960 (Tax). (Article first published in 1959.) Sewall Wright: Evolution: Selected Papers (ESP), ed. William B.Provine, 1986. Sewall Wright: 'Random drift and the shifting balance theory of evolution', in Mathematical Topics in Population Genetics, ed. Kojima, 1970. Labels: Burbridge, Population genetics
Thursday, October 23, 2008
Notes on Sewall Wright: The Shifting Balance Theory - Part 1
posted by
DavidB @ 10/23/2008 03:52:00 AM
Finally, Sewall Wright's Shifting Balance theory of evolution. This will positively, definitely, categorically be my last note on Sewall Wright. Unless I think of something else.
For convenience I will split the note into two parts, one dealing with the theory in its original form, and the second dealing with subsequent developments. Two catch-phrases indissolubly linked with Sewall Wright are the adaptive landscape, and the shifting balance. In preparing my note on Wright's concept of the adaptive landscape I was surprised to discover that Wright himself seldom if ever used this expression. I could not find a single example. I was therefore half-expecting that I would not find any reference to the shifting balance either - and I would have been half-right. Wright did use that term, but not, as far as I can find, until surprisingly late in his long career.... All page references are to Evolution: Selected Papers unless otherwise stated. See the References for details. The first mention of 'the shifting balance' Wright refers extensively to the 'shifting balance theory' in Volume 3 of his treatise Evolution and the Genetics of Populations, published in 1977, but I have not found this term in the first two volumes (1968 and 1969), or in anything else published by Wright before 1970. Nor was it used by authors such as Dobzhansky, Mayr, and Simpson, when describing Wright's ideas. The earliest use of the term I have found is in Wright's article of 1970 on 'Random drift and the shifting balance theory of evolution'. Admittedly, I have not read all of his 200-odd papers published before that year, but unless anyone can unearth an earlier use I suggest that the term was in fact coined in this article of 1970, some 50 years into Wright's career. The terminology of a theory is less important than its substance, but the absence of the term 'shifting balance' before 1970 (if I am right about this) does have two implications: first, we should not expect other authors (such as Fisher and Haldane) to have commented on the 'shifting balance theory' as such, and second, in the absence of a single label, it may not have been perceived as a single unified theory at all. Earlier terminology The apparent absence of the phrase 'shifting balance' before 1970 does not mean that Wright had never previously used the terms 'balance' or 'shifting', sometimes in close proximity. Wright was fond of the term 'balance', and related terms such as 'equilibrium' or 'poise', and used them for a variety of purposes, sometimes with a precise mathematical meaning, and sometimes more loosely. Here are some examples, chronologically arranged: 1931: 'The conditions favorable to progressive evolution as a process of cumulative change are neither extreme mutation, extreme selection, extreme hybridization nor any other extreme, but rather a certain balance between conditions which make for genetic homogeneity and genetic heterogeneity' (96) 1931: 'Evolution as a process of cumulative change depends on a proper balance of the conditions which... make for genetic homogeneity and genetic heterogeneity of the species' (158) 1941: 'The most general conclusion that can be drawn from the attempt to develop a mathematical theory of the simultaneous effects of all statistical processes that affect the genetic composition of populations is that in general the most favorable conditions for evolutionary advance are found when these are balanced against each other in certain ways, rather than when any one completely dominates the situation' (488) 1951: 'The general qualitative conclusion would still seem to hold that this [the evolution of culture] or any other evolutionary process depends on a continuously shifting but never obliterated state of balance between factors of persistence and change, and that the most favourable condition for this occurs when there is a finely subdivided structure in which isolation and cross-communication are kept in proper balance' (596) 1959: 'It is concluded that the most favorable conditions are those of balance: a balance among the directed processes that insures the maintenance of a high degree of heterozygosis in minor factors and a balance between the directed processes as a group and various sorts of random ones that insures extensive random drift around the equilibrium positions of the gene frequencies. All these conditions are met in the highest degree where there is a certain balance between isolation and crossbreeding within each of a large number of local populations of the species' (Tax, 470-1) 1960: 'In developing the balance theory of evolution, I was trying to arrive at a judgement of the most favorable conditions for evolution under the Mendelian mechanism' (619) It will be noted that in the last of these passages Wright refers to the 'balance theory of evolution', and in another the 'balance between factors of persistence and change' is said to be 'continuously shifting'. Wright therefore comes very close to using the phrase 'shifting balance theory', but the fact that even in these passages he does not actually use it strengthens the suspicion that he had not yet coined the term as such. What balance? And what shifts? Many other uses of the terms 'balance' and 'shift' by Wright could be cited. I have quoted only those which come closest to his explicit term 'the shifting balance'. But even these examples, on a careful reading, leave it unclear what is the 'balance' that is seen by Wright as essential to effective evolution. Many different things are said to be 'balanced'. What exactly is a 'balance between factors of persistence and change', and is it the same as 'balance between conditions which make for genetic homogeneity and genetic heterogeneity'? Migration, for example, is a factor usually making for genetic homogeneity, but it is also often a factor making for 'change'. So which side of the balance does it fall on? It might be hoped that in Wright's 1970 article, or in Volume 3 of Evolution and the Genetics of Populations, where the 'shifting balance theory' is discussed at length, we would find a clear statement of the meaning of the term itself. What is the relevant balance, how does it shift, and how does Wright's theory of evolution depend on the shifting of the balance? It may be that the answers are there, but if so, I have not found them. While Wright discusses various component parts of his theory, the overarching term 'the shifting balance' is not itself defined or explained. Moreover, whatever interpretation we give to the term 'balance', it does not seem that the 'shifting' of the balance itself plays any essential part in Wright's conception of the evolutionary process. The balance between the various factors of evolution, including selection, mutation, migration, environment, genetic drift, and population structure - to list the obvious ones - might stay constant, yet the process of evolution as described by Wright could still work, if the balance of factors is right. It is not the shifting of the balance, but the existence of the right kind of balance, which according to Wright is favourable to evolutionary progress. I conclude that the 'shifting balance theory' is a convenient and memorable label, but one without a precise literal meaning in isolation. When was the theory first published? Even if the label 'shifting balance theory' was not adopted until 1970, the doctrines covered by that label may have been propounded earlier. Wright himself, in 1970, claimed to have first published the theory as long ago as 1929. It can be confirmed that some of the key elements of the theory were contained in Wright's great 1931 paper 'Evolution in Mendelian populations', and summarised in shorter related papers beginning in 1929. Notably, these contain several key propositions which Wright maintained consistently to the end of his life: a) The most favourable circumstances for evolution are in large populations subdivided into many small partially isolated populations; b) Large freely interbreeding populations are not favourable to continuing evolution; c) Genetic drift is an important part of the evolutionary process; and d) The differential success of subpopulations, which Wright describes as 'intergroup selection', is an important contributor to cumulative evolutionary change. If we regard these four propositions as constituting the shifting balance theory, then it was indeed first published in 1929. Changes to the theory This does not mean that there were no important changes to the theory after 1929. I believe there were changes both of substance and of emphasis, which I would summarise as follows: 1. In 1932 Wright adopted the metaphor of a multidimensional field of gene combinations and fitness values, which was later described (though not by Wright) as the 'adaptive landscape'. In my view this was more than just an illustrative device. The concept of selective peaks as alternative states of stable equilibrium was a valuable addition of substance to the theory, not corresponding to anything clearly stated in the original version. 2. Whereas in 1929-31 Wright had denied that temporary changes in environmental conditions would have major evolutionary effects, in 1932 he changed his position and accepted that environmental fluctuations could 'shuffle' populations from one evolutionary position of equilibrium to another, usually higher, one. 3. As a consequence of change (2), Wright reduced his emphasis on the importance of genetic drift, which he had originally claimed as essential to long-term evolutionary progress. After 1932 genetic drift was in principle only one of several mechanisms for change. But Wright did not make it sufficiently clear that his position had changed, and did not follow through the implications of the change for his views on the importance of population structure. 4. Throughout his career Wright maintained that the evolutionary process was partly adaptive and partly non-adaptive or 'random', but the emphasis he put on these elements shifted from the non-adaptive aspect to a greater emphasis on adaptation. 5. In his later writings on the subject Wright identified three 'phases' in the shifting balance process, but these are much less clear in the earlier versions of the theory. Some but not all of these changes have already been identified in William Provine's admirable biography of Wright. The remainder of this note will mainly be concerned with documenting the various changes. The original version of the theory (1929-31) The key propositions of the original version of the theory were conveniently summarised by Wright himself in a short paper of 1929, which I will quote in full: The frequency of a given gene in the population is affected by mutation, selection, migration and chance variation. The pressure exerted by these factors (excluding chance) and the position of equilibrium between opposing pressures are easily found. Gene frequency fluctuates about this equilibrium in a distribution curve, determined by size of population and the various pressures. The mean and variability of characters, correlation between relatives and the evolution of the population, depend on these distributions. In too small a population, there is nearly complete random fixation, little variation, little effect of selection and thus a static condition, modified occasionally by chance fixation of a new mutation, leading to degeneration and extinction. In too large a freely interbreeding population, there is great variability, but such a close approach of all gene frequencies to equilibrium that there is no evolution under static conditions. Changed conditions cause a usually slight and reversible shift of the gene frequencies to new equilibrium points. With intermediate size of population, there is continual random shifting of gene frequencies and consequent alteration of all selection coefficients, leading to relatively rapid, indefinitely continuing, irreversible and large fortuitous but not degenerative changes even under static conditions. The absolute rate, however, is slow, being limited by mutation pressure. Finally, in a large but subdivided population, there is continually shifting differentiation among the local races, even under uniform static conditions, which through intergroup selection brings about indefinitely continuing, irreversible, adaptive and much more rapid evolution of the species as a whole. (78) These propositions are all stated more fully and supported by arguments in the 1931 papers 'Statistical theory of evolution' and 'Evolution in Mendelian populations'. (Although 'Statistical theory of evolution' was published first, it seems that 'Evolution in Mendelian populations' was completed first and 'Statistical theory of evolution' written as a summary of it.) Some of them are also covered in Wright's 1930 review of Fisher's Genetical Theory of Natural Selection. Most of them are restated and defended throughout Wright's career. The arguments given by Wright to support the key propositions (quoted in italics from the 1929 article) can be summarised as follows: In too small a population, there is nearly complete random fixation, little variation, little effect of selection and thus a static condition, modified occasionally by chance fixation of a new mutation, leading to degeneration and extinction. For this purpose 'too small' a population is one in which 1/4N (where N is the effective population size) is much larger than selection and mutation rates. (148) In this case genetic drift will be the main factor in evolution. Most genes will soon be fixed, there will be little variation within each population, and random unadaptive changes will lead to extinction. (93, 142, 148) In too large a freely interbreeding population, there is great variability, but such a close approach of all gene frequencies to equilibrium that there is no evolution under static conditions. For this purpose 'too large' a population is one in which both selection and mutation rates are much larger than 1/4N. (148) In this case, genetic drift will have little effect, and gene frequencies will be determined by the balance of selection and mutation. If selection on a gene is much stronger than mutation pressure, there will be almost complete fixation at each locus and therefore no evolution under fixed conditions. (148-50) If selection is not much stronger than mutation pressure, there will be more genetic diversity, but all gene frequencies will be close to equilibrium and evolution will be very slow unless conditions change. (150) Note that these arguments tacitly assume that there are no new favourable mutations, or existing ones still under selection. Changed conditions cause a usually slight and reversible shift of the gene frequencies to new equilibrium points. In 'Statistical theory of evolution' Wright says that 'Changes in conditions should be followed by systematic changes in gene frequencies until all have reached the new positions of equilibrium. Return to the old conditions should be followed by return to the old equilibria' (92). No specific reason is given for this conclusion. In 'Evolution in Mendelian populations' the explanation is slightly fuller. Following a strengthening of selection, gene frequencies will change, but 'The rapid advance has been at the expense of the store of variability of the species and ultimately puts the latter in a condition in which any further change must be exceedingly slow. Moreover, the advance is of an essentially reversible type. There has been a parallel movement of all the equilibria affected and on cessation of the drastic selection, mutation pressure should (with extreme slowness) carry all equilibria back to their original positions. Practically, complete reversibility is not to be expected, and especially under changes in selection which are more complicated than can be described as alternately severe and relaxed. Nevertheless, the situation is distinctly unfavorable for a continuing evolutionary process' (150). Note that Wright does not claim the changes are always reversible, only that this is 'essentially' or 'usually' the case. Bur he gives no clear reasons for this position, and only a year later (1932) he abandons it. As this is one of the major developments in the theory I consider it more fully in Part 2 of this note. With intermediate size of population, there is continual random shifting of gene frequencies and consequent alteration of all selection coefficients, leading to relatively rapid, indefinitely continuing, irreversible and large fortuitous but not degenerative changes even under static conditions. The absolute rate, however, is slow, being limited by mutation pressure. For this purpose an intermediate size of population is one where, for many genes, the selection pressure is not much stronger than the mutation rate, and neither selection pressure not mutation rate are much higher than 1/4N (150-1). (Since mutation rates were known by Wright not to be much higher than 1 in 100,000, this implies an effective population size of the order of 25,000.) In these circumstances genetic drift will be strong enough to cause considerable fluctuation in gene frequencies, but not to lead to rapid fixation of genes and loss of genetic diversity. Wright describes the result as 'a kaleidoscopic shifting of the average characters of the population through predominant types which practically are never repeated' (95, see also 151). But Wright emphasises that it would be a very slow process, as 'hundreds of thousands of generations are required for important evolutionary changes' (95). He mentions the effect of mutation rates as limiting the speed of change (78, 95, 151), presumably because with mutation rates not very different from the rate of genetic drift, mutation pressure tends to maintain genetic uniformity. But surely the main reason for slowness is that genetic drift itself is very slow in a population of many thousands. Finally, in a large but subdivided population, there is continually shifting differentiation among the local races, even under uniform static conditions, which through intergroup selection brings about indefinitely continuing, irreversible, adaptive and much more rapid evolution of the species as a whole. This is the most important proposition of the shifting balance theory in its original form. Wright never abandoned his view that a large subdivided population is most favourable to evolution. The subdivisions must be small enough, and isolated enough from each other, that the subpopulations can diverge in gene frequencies (151-2). Curiously, there is an important difference between Wright's accounts in his two 1931 presentations of the theory. In 'Statistical theory of evolution' Wright mentions only 'random drift' as causing the divergence between subpopulations, with the result that there is a 'geologically rapid drifting apart of the various sub-groups, even under uniform conditions. This is a non-adaptive radiation, but, on the average, not such as to lead to appreciable deterioration' (95). In 'Evolution in Mendelian populations', on the other hand, Wright mentions both genetic drift and local variation in selection pressures, so that the result is 'a partly nonadaptive, partly adaptive radiation among the subgroups' (151). There is of course no reason why both processes should not occur at once, perhaps in different subgroups or at different loci in the same subgroups at the same time. But the difference does have implications for the final phase of the process, which is 'intergroup selection'. On this, Wright says that 'Those [subgroups] in which the most successful types are reached presumably flourish and tend to overflow their boundaries while others decline, leading to changes in the mean gene frequencies of the population as a whole' (152). But if adaptive variation among subgroups is due only to local circumstances of selection (as seems to be suggested in 'Evolution in Mendelian populations'), those types which have highest fitness in their own locality cannot be expected to succeed elsewhere. If on the other hand the variation among subgroups is purely due to random drift (as seems to be suggested in 'Statistical theory of evolution'), it is not obvious that they will differ significantly in fitness for genetic reasons. 'Statistical theory of evolution' does however contain a very important development or clarification of the theory: 'Exceptionally favorable combinations of genes may come to predominate in some of the subgroups. These may be expected to expand their range while others dwindle. This process of intergroup selection may be very rapid as compared with mass selection of individuals, among whom favorable combinations are broken up by the reduction-fertilization mechanism in the next generation after formation' (95). The reference to 'favorable combinations' here is the first sign of the emphasis on epistatic fitness interactions which becomes increasingly important in the later development of the theory. But in the original statement, in 1931, it comes out of the blue and unsupported by any detailed analysis. Likewise, the concept of 'intergroup selection' is not explored in any depth, and the claim that it would be more rapid than 'mass selection of individuals' is little more than a bare assertion. The suggested advantage that 'favorable combinations' are not immediately broken up by sexual reproduction seems to require not only a high degree of genetic unity within the subgroups, but the maintenance of that unity during the process of 'intergroup selection', despite the probable intermingling of different groups. The credibility of this process has been one of the main areas for recent controversy and research on the shifting balance theory. It should incidentally be stressed (see also Provine, p.288) that 'intergroup selection' as envisaged by Wright has little to do with 'group selection' as envisaged by most of its recent advocates. Wright does not suggest that successful groups have evolved adaptations for group living, or that their members behave 'altruistically' towards each other (though his theory does not exclude this either, and he later made some comments in this direction). His claim is rather that the subdivided population structure allows some groups, by chance, to form combinations of genes that are advantageous to individual fitness. The higher mean fitness of the groups is the resultant of these individual fitness advantages. Wright also gives mixed messages about the adaptiveness of the process. While repeatedly claiming that in the long run the process is adaptive, Wright accepted the common view of many biologists at the time that the differences between subspecies and even between species of the same genera are usually non-adaptive (154, see also Provine p.288-99), a view which would seem to require the adaptive process of 'intergroup selection' to occur mainly between different genera or even higher taxa! But in this case 'intergroup selection' between small subgroups of the same species would be irrelevant to the process. Yet in 'Evolution in Mendelian populations' Wright also suggests that intergroup selection within the species may be responsible for 'peculiar adaptations' and 'extreme perfection' (154-5), a claim which is not, I think, repeated anywhere else. Overall, the emphasis in these early writings is more on the nonadaptive than the adaptive aspects of the process. Taking stock Before exploring the subsequent development of the theory (in Part 2), I will try to take stock of the position reached by 1931. Already in his summary note of 1929 Wright had stated some of the key propositions of the shifting balance theory. In the two articles of 1931 he began the task of justifying these propositions. The arguments he put forward were ingenious, stimulating, and not implausible, but far from conclusive. There were moreover a number of tensions, if not actual inconsistencies, within Wright's accounts. One of these concerned the extent to which the process was adaptive, as has been explored fully by Provine. Another is the respective roles of genetic drift and local selection, on which I have pointed out an apparent difference between the two articles of 1931. Another is the problem of migration between groups. As suggested in my earlier note on migration, Wright did not attempt to quantify the effects of migration until after he had committed himself to the importance of random drift within semi-isolated subgroups. Only then, in 1929, did he discover 'that isolation in districts must be much more nearly complete than I realized at first' for the process to work. 'Evolution in Mendelian populations' makes an attempt to remedy the deficiency (128), but further work was clearly needed. Several important aspects of the theory in its mature form are also lacking from the original version. Notably, there is nothing clearly corresponding to Wright's later emphasis on alternative local optima - 'selective peaks' - available to populations or subpopulations. These local optima depend heavily on epistatic fitness interactions, which are hardly mentioned in the original version. In the mature theory, subpopulations 'explore' the field of possibilities under the influence of random factors (genetic drift, but also environmental fluctuations) until they wander into the zone of attraction of a new selective peak. The stage of 'exploration' is Phase 1 of the process, while the climbing of the population up a peak is Phase 2, and intergroup selection is Phase 3. In the original version of the theory there is no clear distinction between Phase 1 and Phase 2, because there is nothing to suggest that the process of 'exploration' ever stops, short of the exhaustion of genetic variation by random fixation of genes. The phrase 'continually shifting differentiation' seems inconsistent with any sharp distinction between two phases. The first signs of a new approach are to be found in 'Statistical theory of evolution', with its reference to some groups finding 'exceptionally favorable combinations of genes', implying epistatic peaks of fitness. Quite possibly this had been in Wright's mind all along, but I do not think it can be identified in anything written before 'Statistical theory', including the much more widely read 'Evolution in Mendelian populations'. Another important omission is any serious discussion of the probability of favourable new mutations. Wright's negative assessment of the prospects for evolution in large freely interbreeding populations depends on the tacit assumption that new mutations can be neglected. Wright later developed arguments to support this position. Overall, a careful reader of Wright's publications up to 1931, without knowledge of subsequent developments, might reasonably conclude that Wright had put forward a remarkably original, ingenious, and comprehensive theory of evolution, consistent with most of what was then believed about the observed pattern of evolution, and free of any obvious fatal defects. This is itself was a very major achievement. But the same reader might also think that the theory was sketchy and speculative, and in need of further elaboration, not to mention empirical tests. Wright himself was no doubt aware of this, and continued to develop the theory for another 50 years, as I will discuss in Part 2. References William B. Provine, Sewall Wright and Evolutionary Biology, 1986. Sewall Wright: 'Physiological genetics, ecology of populations, and natural selection', in Evolution After Darwin, vol. 1, ed. Sol Tax, 1960 (Tax). (Article first published in 1959.) Sewall Wright: Evolution: Selected Papers (ESP), ed. William B.Provine, 1986. Sewall Wright: 'Random drift and the shifting balance theory of evolution', in Mathematical Topics in Population Genetics, ed. Kojima, 1970. Labels: Burbridge, Population genetics
Sunday, October 12, 2008
My post here discussed Sewall Wright's concept of the adaptive landscape, and a post here discussed R. A. Fisher's views on the subject. Before I come to my planned note on Sewall Wright's Shifting Balance theory, there are some points about adaptive landscapes which didn't fit easily into the earlier posts...
Terminology As mentioned in the post on Wright's 'landscapes', he used two different versions of a multi-dimensional model of fitness. In one interpretation the dimensions, except for that of fitness, represent the number of alleles of different types in an individual genotype. I will call this a genotype landscape. In the other interpretation, the dimensions except for that of fitness represents the proportion of alleles of different types in a population. I will call this a frequency landscape. Both interpretations can be called genetic landscapes. While Wright's interpretations always have genetic dimensions, other authors have used concepts in which the dimensions of the landscape represent phenotypic or ecological variables. I will call these phenotype landscapes. Peaks in such a landscape represent optimal phenotypes or ecological niches. In both genetic and phenotype landscapes one of the dimensions usually represents reproductive fitness, but some alternative measure of adaptation may be used. For example if the phenotype is the shape of a fish, the measure of adaptation might be some aspect of swimming efficiency. Some authors draw a distinction between a fitness landscape and an adaptive landscape, but the distinction is not consistently used. For example, according to Gavrilets (p.30) these terms are used to designate what I have called genotype and frequency landscapes respectively, but McGhee (p.1) uses them to designate genetic and phenotype landscapes. Most authors seem to use the terms 'adaptive landscape', 'fitness landscape', 'genetic landscape', and 'selective landscape' interchangeably, though each of them may also have other meanings. (For example, 'genetic landscape' may be used to describe the geographical distribution of genes.) Anyone searching for relevant studies should try all of these variants. I will use adaptive landscape as a general term embracing all of them. Literature There are at least two recent books devoted to adaptive landscapes, by Gavrilets and McGhee (see refs.). Gavrilets deals mainly with genetic landscapes, McGhee with phenotype landscapes. The book by Gavrilets has an extensive bibliography, which provides a good way into the literature on genetic landscapes. The studies I have looked at deal mainly with genotype landscapes. There seems to be comparatively little work on frequency landscapes, perhaps because the subject is less amenable to study by computer simulation. The number of peaks in genotype landscapes There is an extensive literature on the number of peaks in genotype landscapes, mainly based on the work of Stuart Kauffman. To begin with, consider a model devised by Kauffman and Levin (1987). Suppose a genome has N loci. For simplicity, assume the loci are haploid and that there 2 possible alleles at each locus. There are therefore 2^N possible different genotypes. Now, suppose that each distinct genotype has a fitness which is independent of the fitness of any other genotype. We may then represent the fitnesses by numbers chosen at random (Kauffman and Levin use the range of rational numbers between 0.0 and 1.0). For simplicity we stipulate that no two genotypes have exactly the same fitness. If we choose one of the 2^N possible genotypes at random, there are N other genotypes which can be derived from that chosen genotype by varying an allele at a single locus. We call these the neighbours of the chosen genotype. The chosen genotype is a local optimum if it has higher fitness than all of its neighbours. But by the stated assumptions the fitnesses of the N + 1 genotypes concerned are random numbers, each of which must have a probability of 1/(1 + N) of being the largest in the set. There is therefore a probability of 1/(N + 1) that the chosen genotype is a local optimum. But the chosen genotype is randomly chosen from the 2^N possible genotypes, and any other genotype (by the given assumptions) would have an equal chance of being a local optimum within its own 'neighbourhood'. Since there are 2^N possible genotypes in total, the total expected number of local optima in the system is therefore (2^N)/(N + 1) [Note 1]. It is obvious that this number increases rapidly with increasing N. It is equally obvious that the assumption of independent fitnesses for each possible genotype is biologically unrealistic. It implies that no single locus, or combination of fewer than N loci, has any predictable effect of its own on fitness. As an extreme alternative to this, suppose that each locus makes a contribution to fitness which is independent of all other loci. In this case one of the alleles at each locus must be unambiguously fitter than the other allele, regardless of the alleles at other loci. Suppose we designate the fitter of the two alleles by an even number, and the less fit allele by an odd number. It is clear that no genotype containing an 'odd' allele can be a local optimum, because the fitness of the genotype could always be increased by substituting an even allele for the odd one. The only local optimum in the system is therefore the single genotype containing exclusively 'even' alleles, no matter how many genotypes there are in the system. This result can be extended to systems with diploid loci and/or multiple alleles at each locus, provided that one of the alleles at each locus is unambiguously fitter than all other alleles. We could also allow the fitness contribution of a locus to be affected by the alleles at other loci, provided the effect is not so great as to reverse the rank order of fitness of the alleles at each locus. This would be the case, for example, if each allele has a primary effect on one trait which makes a large difference to fitness, and a secondary effect on other traits, provided the secondary effects do not exceed the fitness difference due to the primary effect. Between the two extreme models, there could be a variety of systems in which the rank order of the contributions of loci to fitness is partly but not entirely independent of other loci. Kauffman has devised a framework known as the NK model. [Note 2] In the NK model there are N haploid loci, with 2 possible alleles at each locus, while the fitness contribution of each locus is affected by the alleles at K other loci as well as itself. The fitness contribution of each possible combination of alleles at each such group of K + 1 loci is a random number chosen from the interval 0.0 to 1.0. For any particular assignment of alleles to the K+ 1 loci, this number determines the fitness contribution of the locus in question. The fitness of the genome as a whole, for any particular assignment of alleles to all N loci, is the average of the contributions for each locus. The precise way in which the loci are connected to each other may vary. According to Kauffman (p.55) this usually makes little difference to the outcome. It may be useful to consider a simple special case which is not treated by Kauffman. Suppose we divide the N loci into N/(K + 1) discrete sets (assuming for simplicity that N/(K + 1) is a whole number). Let each of the K + 1 loci in each such set be 'connected' to the remaining K loci in the set. There are 2^(K + 1) possible combinations of alleles for each such set, and let each combination be assigned a fitness value randomly chosen from the interval 0.0 to 1.0. For any particular assignment of alleles to the loci, this number constitutes the fitness contribution of every locus in the set to the fitness of the genome. But each such set of K + 1 loci can be treated as a case of the Kauffman/Levin model, and has an expected number of [2^(K+ 1)]/[K + 2] local optima. Since each such set of loci, by assumption, has no effect on the fitness contribution of any loci outside the set, it follows that any combination of local optima for all of the N/(K + 1) discrete sets will also be a local optimum for the entire genome, since any change at a single locus would reduce the overall fitness of the genome. Since there are ([2^(K+ 1)]/[K + 2])^[N/(K + 1)] such combinations, this is the expected number of local optima for the entire genome. It may be easily checked that for the value K = N - 1, where each locus is connected to every other locus in the genome, this reduces to (2^N)/(N + 1), as in the first of the extreme models, while for K = 0, where no locus is connected to any other locus, it reduces to 1, as in the other extreme model. For values of K between 1 and N - 2, the number of local optima increases with increasing K and/or N. In my simple example the genome is divided into non-overlapping sets of loci. But more generally in the NK model there will be overlap. For example, the sets of connected loci may be arranged cyclically, like abcde, bcdef, cdefg ......zabcd. Or the connections could be chosen at random, in which case there is a non-zero probability that the same locus will enter into more than one set of connected loci. This makes the problem of determining the number of local optima much more complicated. A given set of alleles may be a local optimum with respect to one set of connected loci, but one or more of those alleles may be sub-optimal for another set to which it belongs. In this case, changing one of those alleles will reduce fitness at some loci but increase it at others. The effect on the overall number of local optima for the genome as a whole is not intuitively obvious, and does not seem amenable to calculation by a general formula. Kauffman and others have relied on computer simulations. The most important result is that the number of local optima increases rapidly with increasing N and/or K (Kauffman p.60). This is not surprising, but it may be taken as vindicating Sewall Wright's intuition that in genotype landscapes with a lot of epistatic relations, the number of selective peaks will be very large. In general one may say that for a realistic size of genome (i.e. with thousands of loci) the number of peaks will be very large unless the value of K (averaged over the genome) is close to zero. Kauffman's NK model is in many ways simplistic, but it does seem quite robust as a basis for exploring the theory of genotype landscapes. Other researchers have developed it in various ways. I don't know (or understand) this work well enough to summarise it, but I recommend the book by Gavrilets, which applies the theory to the problem of speciation. He notably claims that if a sufficient proportion of alleles are allowed to be selectively neutral, then in genotype landscapes of high dimensionality there will usually be a 'network' of ridges connecting the peaks, and along which populations can evolve without crossing fitness 'valleys'. The number of peaks in frequency landscapes As noted earlier, there seems to be much less work on frequency landscapes. In my post on Fisher I mentioned that in private letters Fisher argued that as the number of dimensions rises, the proportion of 'level points' which are all-round maxima will fall, and will be about 1/2^N of the total, where N is the number of dimensions. Fisher may have assumed that (a) in each dimension of gene frequencies, only about half of the level points will be maxima, and (b) the location of the maxima in each dimension is usually independent of the other dimensions. [Note 3] With these assumptions, the probability that a level point will be simultaneously maximal in all dimensions will only be about (1/2)^N, or 1 in 2^N, as suggested by Fisher. It does not follow that the number of maxima would not rise. If the number of level points in a single dimension is n, the expected number of level points in N independent dimensions would be n^N, so the expected number of all-round maxima would be (n^N)/2^N. For any n much greater than 2, this will increase rapidly with increasing N; for example, if n = 4, the number of maxima for N = 2, 3, 4.... will be 4, 8, 16... which rapidly becomes enormous. The validity of the two key assumptions - that about half of the level points in each dimension will be maxima, and that these will be independent of each other - is debatable. First, if we consider loci without epistasis, there are three cases. If one homozygote is superior to the other, while the heterozgyote is either intermediate in fitness or equal to one of the homozygotes, then there will be one maximum and one minimum in the relevant dimension. If the heterozygote is superior to both homozygotes, there will be one maximum and two minima. If both homozygotes are superior to the heterozygote, there will be two maxima and one minimum. There are no cases in which there would be more than two minima or maxima. (If there are more than two alleles at the locus the possibilities are more complicated, but it is difficult to think of realistic scenarios in which there are more than two maxima or minima in each dimension.) For loci without epistasis the assumption that about half of the level points in each dimension will be maxima is therefore plausible as a rough average. But for loci with epistasis the key assumptions are doubtful. The assumption of independence for each dimension is no longer generally valid, as the fitness for all the interacting loci has to be considered simultaneously. For the important case of two interacting loci under selection for an intermediate phenotype (see the post on Wright) there will be two maxima, two minima, and only one saddle point. The key assumptions therefore do not hold even approximately in this case, and if it is at all common, the number of all-round maxima for the genome as a whole may be very large. It has indeed been claimed (Gavrilets p.37) that the number of maxima is bound to rise with the number of dimensions. But as already discussed in connection with Kauffman's systems, there is no necessity about this: it is quite easy to conceive of a system with only one all-round maximum. The accessibility and stability of peaks From an evolutionary point of view, what is important is not just the number of adaptive peaks, but whether they are accessible to the population - i.e. whether the population will evolve towards them - and whether, if the population reaches them, they will be stable under disturbances such as temporary changes in the environment or influxes of migrants. For both purposes, in a frequency landscape we need to consider the 'zone of attraction' of the peaks, i.e. the range of gene frequencies within which the population will move towards the peak under the influence of natural selection. I have not found much discussion of this issue in the literature (which, as I have said, deals mainly with genotype rather than frequency landscapes), but a few general points seem clear. First, we expect that, other things being equal, higher peaks will have wider zones of attraction. In geometrical terms, if two solid figures have the same shape, the taller figure will have the larger base. In genetic terms, the higher the fitness of a genotype relative to the average fitness of the population, the wider will be the range of gene frequencies within which the genes making up that genotype will be positively selected. Second, peaks will have a wider zone of attraction if their component genes have an advantage in the heterozygote as well as the homozygote state. If the optimum genotypes contain recessive homozygotes, the genotypes will be rare, and therefore will not contribute much to the fitness of their component alleles, until the relevant alleles are already frequent in the population. Third, even if a peak has very high fitness, it will not have a wide zone of attraction if the high fitness depends on the epistatic combination of a large number of alleles which do not otherwise have a fitness advantage. In such a case, the advantageous combinations will not appear with significant frequency in the population until all of the component genes already have a high frequency. The peak will be like a spike with a narrow base. Such a peak will be neither easily accessible nor stable, since even if the peak is reached, any fluctuation in the landscape is liable to push the population out of the zone of attraction. Finally, whether or not a peak is easily accessible to a population depends on the population's current gene frequencies. Here it should be noted that in most of the plausible scenarios for multiple fitness peaks, such as Wright's favourite example of traits under stabilising selection, some of the alleles in the optimum genotypes will (at the peak) be fixed in the population, with alternative peaks at opposite sides or corners of the landscape. (This fact tends to be obscured by illustrative diagrams, including Wright's, which usually show peaks somewhere in the middle of landscape.) If alleles are fixed, the population can only move to another peak if new alleles are introduced by mutation or migration. These new alleles will be opposed by selection unless the environment changes so that the peak itself shifts. In order to move to another peak without migration or a change in environment, a long period of genetic drift, opposed by selection, will be required unless the population is very small. This is one of the key issues of credibility with Wright's shifting balance theory in its original form. Note 1: Kauffman and Levin, pp.20-21. There might be a suspicion of fallacy somewhere in this argument, as the probability that a genotype is a local optimum is not independent of the probability for other genotypes. It would certainly be fallacious to conclude that there is a probability [1/(N + 1)]^[2^N] that all of the genotypes are local optima, since this is impossible. However, Kauffman and Levin's formula for the number of local optima appears to be valid. Note 2: Kauffman p.42. Kauffman's description of the model is very concise and not ideally clear, partly because of ambiguity in his use of the terms 'gene', 'allele' and 'locus'. But I think my interpretation is consistent with what Kauffman and others say about the NK model. Note 3: since Fisher gave no reasons for his claim, this is just speculation. He may quite possibly have had other reasons, but didn't spell them out. In his statistical work Fisher was very familiar with applications of N-dimensional geometry, so he would have had a better understanding than most people of the properties of high-dimensional landscapes . References Sergey Gavrilets, Fitness Landscapes and the Origin of Species, 2004. Stuart Kauffman, The Origins of Order, 1993 Stuart Kauffman and Simon Levin, 'Towards a general theory of adaptive walks on rugged landscapes', J. Theoretical Biology, 1987, 128, 11-45. George R. McGhee, The Geometry of Evolution: Adaptive Landscapes and Theoretical Morphospaces, 2007 Labels: Burbridge, Population genetics
Wednesday, October 01, 2008
Readers who lived through the Punctuated Equilibrium controversy of the 70s and 80s will recall that it petered out rather inconclusively, largely for lack of decisive empirical evidence one way or the other. The fossil record is seldom good enough to distinguish unambiguously between punctuational and gradual modes of evolution, one problem (noted already by Darwin) being that the sudden appearance of a new form in a given locality may result from migration rather than rapid evolution in the same place.
Given these difficulties, a disproportionate amount of attention was focused on a handful of examples that seemed to show good evidence either of punctuational or gradual evolution. One of the best examples on the punctuationist side of the debate was a study of molluscs in the Turkana Basin of Africa by P. G. Williamson [Note 1] Williamson's study was criticised at the time on various grounds - for example that the changes observed might be due to environmental stress rather than genetic evolution - but the critics did not produce new evidence from the field. That is changed by an article [Note 2] by a Dutch team in a recent issue of the journal Evolution.... The Abstract of the article is as follows: A running controversy in evolutionary thought was Eldredge and Gould's punctuated equilibrium model, which proposes long periods of morphological stasis interspersed with rapid bursts of dramatic evolutionary change. One of the earliest and most iconic pieces of research in support of punctuated equilibrium is the work of Williamson on the Plio-Pleistocene molluscs of the Turkana Basin. Williamson claimed to have found firm evidence for three episodes of rapid evolutionary change separated by long periods of stasis in a high-resolution sequence. Most of the discussions following this report centered on the topics of (eco)phenotypy versus genotypy and the possible presence of preservational and temporal artifacts. The debate proved inconclusive, leaving Williamson's reports as one of the empirical foundations of the paradigm of punctuated equilibrium. Here we conclusively show Williamson's original interpretations to be highly flawed. The supposed rapid bursts of punctuated evolutionary change represent artifacts resulting from the invasion of extrabasinal faunal elements in the Turkana palaeolakes during wet phases well known from elsewhere in Africa. I have read the full article (available here), which looks convincing on this particular case (but what do I know about old African molluscs?) [Added: a more easily readable pdf version is also available. Google 'bocxlaer turkana' and you should find it.] The strongest point is that it is not just armchair criticism but based on extensive new fossil collecting. But since I specialise in armchair criticism I can hardly throw any stones. Obviously one such case doesn't disprove punctuated equilibrium, but Williamson's study was in some ways the 'poster child' for the theory (more so than even Eldredge and Gould's own studies), so its demolition (if accepted) would be a serious blow. Note 1: P. G. Williamson, 'Palaeontological documentation of speciation in Cenozoic molluscs from Turkana Basin', Nature, 1981, 293, pp.437-43. Also reprinted in Evolution Now, ed. John Maynard Smith, 1982. I can't find any publications by Williamson after 1990, and I believe I have read somewhere that he died at a sadly early age. My apologies if I am mistaken. Note 2: Bert van Bocxlaer, Dirk van Damme, and Craig S. Feibel, 'Gradual versus punctuated equilibrium evolution in the Turkana Basin molluscs: evolutionary events or biological invasions?', Evolution, 2008, 62, pp.511-20. Labels: Burbridge, Population genetics
Saturday, September 27, 2008
In my note on Sewall Wright's concept of the Adaptive Landscape I said that I would later discuss R. A Fisher's views on the subject. Some commentators have claimed that Fisher held a definite view on the 'shape' of the landscape. For example, a book by Sergey Gavrilets includes a section on 'Fisher's single-peak fitness landscapes', with the claim that:
In contrast to Wright, Fisher... suggested that as the number of dimensions in a fitness landscape increases, local peaks in lower dimensions will tend to become saddle points in higher dimensions. In this case, according to Fisher, natural selection will be able to move the population without the need for genetic drift or other factors. A typical fitness landscape implied by Fisher's views has a single peak. - Gavrilets, p.36 I think this goes beyond anything that Fisher actually says about Wright's adaptive landscape. There is of course room for debate about what an author's views imply. My own interpretation is that Fisher was sceptical about the value of the landscape concept as such, because both environmental and genetic conditions were too changeable for the metaphor of a 'landscape' to be useful. For Fisher the question of the 'shape' of the landscape therefore did not arise as a major issue, and he had no need to take a firm view on it. I discuss this interpretation below the fold. Sources As I pointed out in my earlier note, Wright himself seldom if ever used the term 'landscape', so we should not expect to find the term in Fisher either. Wright usually referred to a 'field' of gene combinations, and a 'surface' of selective values. He used these concepts mainly to illustrate his shifting balance theory of evolution. Any comments by Fisher that are relevant to the shifting balance theory could therefore also be relevant to the landscape concept. Even with this broad scope, I can find few published comments by Fisher on the subject. The main ones are in his 1932 review of Wright's paper on 'Evolution in Mendelian Populations', reprinted in Bennett (ed.), his 1941 paper on 'Average excess and average effect of a gene substitution', his 1953 paper on 'Population genetics', and his 1958 paper on 'Polymorphism and natural selection', all available at the Fisher Archives here. In addition to Fisher's published writings, his correspondence contains a few relevant remarks. Most of his correspondence is accessible at the Fisher Archives, and a good selection of his letters on evolution and genetics is published in Bennett (ed.) Two letters are especially relevant. In February 1931 Wright outlined his landscape concept in a letter to Fisher, quoted in Provine's biography of Wright (p.272). In a reply Fisher made some sceptical comments. Then in 1938 Fisher's colleague E. B. Ford described Wright's concept in a popular book on genetics. In a letter of 2 May 1938 to Ford, commenting on his book, Fisher gave what is probably his longest critique of the landscape concept. The letter is published in Bennett (ed.) (p.201-2) and available at the Fisher Archives, so I will not quote it in full, but it should certainly be read by anyone interested in this issue. From Fisher's published and unpublished writings we can extract a number of criticisms of Wright's theory. The interpretation of the dimensions of the landscape In his biography of Wright, William B. Provine has pointed out that Wright in various places used two different interpretations of the genetic 'dimensions' of the landscape, which in Provine's view are inconsistent (Provine, p.313). In one interpretation the dimensions represent the number of alleles of a given type in an individual genome, while in the other interpretation they represent the frequency of those alleles in a population. Provine points out that in the first interpretation there is properly speaking no continuous surface, but only a lattice of discrete points. He also argues that there is no way of validly transferring conclusions from one interpretation to the other. I believe that these criticisms are somewhat overstated, but it is interesting to find that they are both anticipated by Fisher. In his letter to Ford, Fisher comments that either Ford's description of Wright's views, or the views themselves, are confused, and points out that 'so far as individuals are concerned, there is only a discontinuous aggregate of lattice points, each having its own selective value. There is no continuum of possible values in which we might speak of peaks or maxima.' In his article of 1941, Fisher also criticises one of Wright's own accounts, remarking that Wright 'confuses the number of genotypes, e.g. 3^1000, which may be distinguished among individuals, with the continuous field of variation of gene frequencies.... the large number of genotypes gives no reason for thinking that even one peak, maximal for variations of all gene ratios should occur in this field of variation' (1941, p.378). It is surprising that no-one else seems to have picked up on the apparent confusion in Wright's accounts until Provine's book in 1986. The number of peaks As discussed in my earlier post, Wright believed that there are usually a very large number of local fitness maxima in the landscape. Fisher, on the other hand, believed that this was unproven. As noted above, he thought that Wright's view was partly due to confusion between optimal genotypes and optimal frequencies. There is no easy transition from the existence of multiple optima among genotypes to multiple optima among frequencies. I have suggested in my earlier post that in some circumstances (notably where the optimal genotype is homozygous at all loci, and fitness is not frequency-dependent) there can be such a transition, but this is a special case. In general Fisher was correct to regard Wright's argument as inconclusive. Fisher makes another criticism in his letters to Wright and Ford. In the letter to Wright he says: In one dimension a curve gives a series of alternative maxima and minima, but in two dimensions two inequalities must be satisfied for a true maximum, and I suppose that only about one fourth of the stationary points will satisfy both. Roughly I would guess that with n factors only 2^-n of the stationary points would be stable for all types of displacement, and any new mutation will have a half chance of destroying the stability. This suggests that true stability in the case of many interacting genes may be of rare occurrence, though its consequence when it does occur is especially interesting and important. In his letter to Ford, Fisher writes: In one dimension, as in a road, we pass over an alternative series of hills and dips, so that half of the level points are maxima. In two dimensions, in addition to peaks and bottoms we have cols [i.e. saddle points], which may be regarded as the lowest points on ridges or the highest points on valleys, the curvature of the ground being positive in one direction and negative in another, and the peaks are only about a quarter of the level spots. In n dimensions only about one in 2^n can be expected to be surrounded by lower ground in all directions. Disregarding for a moment the important comment in the first letter about new mutations, Fisher's thinking seems to be as follows. In each dimension of gene frequencies, only about half of the level points will be maxima. Assuming that the location of the maxima in each dimension is independent of the other dimensions, the probability that a level point will be simultaneously maximal in all dimensions will only be about (1/2)^n, or 1 in 2^n. As these are just comments in private letters, it is difficult to know how much weight we should put on them. Fisher uses the words 'roughly', 'guess', and 'about', which do not suggest a dogmatic position. The validity of the two key assumptions - that about half of the level points in each dimension will be maxima, and that these will be independent of each other - could be discussed at length. But even at best, Fisher's argument only goes to show that the proportion of the level points which are all-round maxima will fall as the number of dimensions increases (which, incidentally, Wright himself accepted, e.g. at ESP p.226). It does not follow that the number of all-round maxima will remain small. If Fisher believed that this was necessarily the case (which is not clear), he was mistaken. It is quite possible that with an increasing number of dimensions the number of level points may increase faster than the proportion of all-round maxima declines. Indeed, it has been claimed that this is generally the case, but this is also unproven. (I will discuss this more fully in a separate post.) I have not found any definite statement by Fisher either accepting or denying the existence of multiple optima. As I pointed out in my post on Fisher's views on epistasis, he accepted that there could be alternative stable allele frequencies at particular loci. As far as I can see, Fisher would not have denied in principle the possibility of multiple optima for the genome as a whole, and indeed his 1931 letter to Wright might be interpreted as accepting them as an important if rare phenomenon. But overall I think Fisher's position should be described as deeply sceptical. Wright himself said that Fisher 'did not accept the concept of multiple selective peaks' (Wright,1970, p.23), which is literally true, provided it is not taken as implying outright rejection either. The mean fitness of the population In Wright's theory, a population is expected to 'climb' up the slope of the fitness landscape under the influence of natural selection, implying that the mean fitness of the population increases. (Selection may however be offset by migration, recurrent mutation, or genetic drift.) In his publications from 1935 onwards (e.g. ESP p.239, 366) Wright uses a formula which may be expressed as delta-q = [q(1 - q)/2W][dW/dq], where q and (1 - q) are the frequencies of two alleles, delta-q is the single-generation change in q, W is the mean fitness of the population, and dW/dq is the partial derivative of W with respect to changes in q. The formula may be interpreted as saying that the effect of selection on the frequency of a particular allele is proportional to its effect on the mean fitness of the population (as well as to the current frequency distribution q(1 - q)). In his 1941 paper Fisher strongly criticised this formulation, showing by a somewhat roundabout argument that it depends on the assumption of random mating, and claiming that any attempt to relate selection pressure to mean fitness is 'foredoomed to failure just so soon as the simplifying, but unrealistic, assumption of random mating is abandoned' (p.378). Wright's derivation of his formula, e.g. at ESP p.239, does indeed assume random mating. But Fisher's objection is not just technical: 'In regard to selection theory, objection should be taken to Wright's equation principally because it represents natural selection, which in reality acts upon individuals, as though it were governed by the average condition of the species or inter-breeding group. Early selectionists, following in this respect the language of the earlier theological writers on organic adaptation, often speak of selection as directed 'for the good of the species'. In reality it is always directed to the good, as measured by descendants, of the individual. Unless individual advantage can be shown, natural selection offers no explanation of structures or instincts which appear to be beneficial to the species. Yet in Wright's equation the whole evolutionary sequence would appear to be governed by the principle of increasing the 'general good'.' (p.378) I think this is somewhat unfair to Wright, who did not ascribe any causal efficacy to the fitness of the population as such, but Fisher's statement is important as his first general criticism of 'good of the species' thinking. He makes similar criticisms in his 1953 and 1958 papers. In the 1958 edition of GTNS a section on 'The Benefit of the Species' is added, which has become highly influential on modern evolutionary thinking. Although this new section does not refer to Wright, it is plausible that Fisher's sharpening of his hostility to 'good of the species' thinking was stimulated by his objections to Wright's equation. New Mutations As already mentioned, in his 1931 letter to Wright, Fisher argues that 'any new mutation will have a half chance of destroying the stability' of an optimal gene frequency. He makes a similar point in his published review of Wright's 1931 paper on 'Evolution in Mendelian Populations', saying that 'even under static conditions, unless it is postulated that the organism is as well adapted as it could possibly be (in which case, obviously, evolutionary improvement is impossible), the equilibrium will be broken by the occurrence of any favourable mutation, of which a steady stream will doubtless occur in one or other of the very numerous individuals produced in each generation. The advantage of the large populations in picking up mutations of excessively low mutation rate seems to be overlooked [by Wright]'. Their attitude towards new mutations is one of the fundamental dividing lines between Wright and Fisher. Wright repeatedly played down the importance of favourable new mutations, on the grounds that their chance of occurring would be negligible even over long periods (see e.g. ESP pp.150, 165, and 321). He seems to have believed that all possible mutations would already have occurred often enough to be selected if they were favourable, so that the possibility of improvement through new mutations would already have been exhausted. Fisher, in contrast, believed that in large populations even very low mutation rates (say, of one in a thousand million per generation) could not be neglected, and that on an evolutionary time-scale of hundreds or thousands of generations they would provide scope for continuing evolution. It may of course be thought that neither Wright nor Fisher, in the 1930s, knew enough about the nature of genes to have any good basis for their opinions. Changing Environment Wright's concept of the adaptive landscape is explicitly based on the assumption of constant environmental conditions. Any change in those conditions involves a change in the landscape itself. Wright was of course aware that environments could change, but he seems to have regarded the 'landscape' as having an underlying continuity of existence even if environmental fluctuations might temporarily change its shape. (I will consider Wright's views on this further in my final post on the shifting balance theory.) Fisher, on the other hand, believed that environmental change was in one sense irreversible. In the section 'Deterioration of the Environment' in GTNS he emphasised especially the organic environment of competitors, etc: For the majority of organisms... the physical environment may be regarded as constantly deteriorating... Probably more important than the changes in climate will be the evolutionary changes in progress in associated organisms. As each organism increases in fitness, so will its enemies and competitors increase in fitness; and this will have the same effect, perhaps in a much more important degree, in impairing the environment, from the point of view of each organism concerned. - The Genetical Theory of Natural Selection, Variorum Edition, ed. Henry Bennett, 1999 p.41-2 In his review of Wright's 'Evolution in Mendelian Populations' (reprinted in Bennett, ed.) Fisher again emphasised environmental change: Professor Wright considers that: 'In too large a freely interbreeding population there is great variability, but such a close approximation to complete equilibrium of all gene frequencies that there is no evolution under static conditions'. He therefore argues that the subdivision of species into partially isolated local races of small size is an important condition not merely, as is obvious, for fission into distinct species, but for progressive evolution. This conclusion is much more debatable [Fisher then makes his point about the importance of new mutations even under static conditions]... Moreover, static conditions in the evolutionary sense certainly do not occur, for, apart from geological and climatological changes, the evolutionary progress of associated organisms ensures that the organic environment shall be continually changing In short, as several recent commentators have noted, Fisher held a 'Red Queen' conception of evolution, in which organisms have to keep constantly running just to keep up with the competition. This is quite alien to Wright's conception, in which under the influence of selection alone the organic world would soon grind to an evolutionary halt. The extent to which either of these views is correct is a matter for empirical observation. Genetic studies of living populations tend to show continual change, at least at a microevolutionary level, which might seem to support Fisher's view, whereas paleontologists often claim to observe long-term stasis in morphological traits, which might support Wright. This is of course one of the points at issue in the debate over 'punctuated equilibrium', which seems to have petered out through boredom (and the death of some key participants) rather than being resolved. A possible explanation of the apparent conflict of evidence is that traits in hard body parts may be more tightly constrained by stabilising selection than biochemical and behavioural traits. For other suggestions see Williams, Chapter 9. Refs: J. H. Bennett, ed.: Natural Selection, Heredity and Eugenics: Including selected correspondence of R. A. Fisher with Leonard Darwin and others, 1983. Sergey Gavrilets, Fitness Landscapes and the Origin of Species, 2004. William B. Provine, Sewall Wright and Evolutionary Biology, 1986. Sewall Wright: Evolution: Selected Papers (ESP), ed. William B.Provine, 1986. George C. Williams: Natural Selection: Domains, Levels, and Challenges, 1992. Sewall Wright: 'Random drift and the shifting balance theory of evolution', in Mathematical Topics in Population Genetics, ed. Kojima, 1970. Labels: Burbridge, Population genetics
Tuesday, September 23, 2008
W. D. Hamilton is rightly given the main credit for establishing the concept of inclusive fitness. He gave it its name, developed its mathematical theory, and examined a wide range of empirical evidence for it.
There had of course been occasional anticipations of inclusive fitness, going back to Darwin's treatment of neuter social insects in the Origin. Hamilton himself mentioned three such partial anticipations: by G. C. Williams, by J. B. S. Haldane, and by R. A. Fisher in his treatment of the evolution of distastefulness among insects (Hamilton, Narrow Roads of Gene Land, vol. 1, pp.49-50). Curiously, neither Hamilton nor many other commentators seem to have noticed a more general and prominent formulation of the concept by Fisher in the Genetical Theory of Natural Selection...... In Chapter 2 of that book, on the 'Fundamental Theorem of Natural Selection', there is a section headed 'Reproductive Value', which contains the following passage (with emphasis added): We may ask, not only about the newly born, but about persons of any chosen age, what is the present value of their future offspring; and if present value is calculated at the rate determined before [in the section on the 'Malthusian Parameter'], the question has a definite meaning - To what extent will persons of this age, on average, contribute to the ancestry of future generations? The question is one of some interest, since the direct action of Natural Selection must be proportional to this contribution. There will also, no doubt, be indirect effects in cases in which an animal favours or impedes the survival or reproduction of its relatives; as a suckling mother assists the survival of her child, as in mankind a mother past bearing may greatly promote the reproduction of her children, as a foetus and in less measure a sucking child inhibits conception, and most strikingly of all in the services of neuter insects to their queen. - The Genetical Theory of Natural Selection, Variorum Edition, ed. Henry Bennett, 1999 p.27 What Fisher here describes as 'indirect effects' may be considered a concise but very general statement of what was later defined by Hamilton as inclusive fitness. Fisher's brief remark may have been overlooked, not only because the statement is not mathematically quantified, but because Fisher immediately goes on to say that 'such indirect effects will in very many cases be unimportant compared to the effects of personal reproduction', and he does not discuss them further. He therefore treats them essentially as a complication to be mentioned but cleared out of the way. Nevertheless, he does recognise the existence of such indirect effects (both positive and negative) and mentions several examples which have later been extensively treated by Hamilton and other sociobiologists. I dare say that someone somewhere has already noticed and mentioned this passage of Fisher, but as it does not seem to be widely known it will do no harm to mention it again. Labels: Burbridge, Population genetics
Wednesday, September 17, 2008
A while ago I posted two notes on R. A. Fisher's views on population size: Part 1 here and Part 2 here. I assembled some evidence from The Genetical Theory of Natural Selection suggesting that Fisher believed the population size of a species was usually between a million and a million million, with the latter figure being a realistic possibility for some species of small invertebrates.
In writing that post I could not find any more direct evidence, so I am pleased to have come across a letter from Fisher to C. Tate Regan, dated 7 February 1927, containing the following explicit statement: The population number of 10^6 [1,000,000] parents in each generation represents a somewhat small species. I suppose most species lie between 10^6 and 10^12 [1,000,000,000,000], although some, such as some of the millipedes, certainly exceed the latter figure. The larger the population the less frequent need mutations be to maintain a given stock of segregating factors, or in other words, with the same mutation rates the larger will the variance (when equilibrium is attained) be. (Bennett, ed., p.255) Earlier in the letter Fisher makes it clear that he is thinking about genes that are nearly neutral in their effect, so that variance is maintained by a balance between mutation and drift. A population of a million million does seem very large, but Fisher's reference to millipedes confirms that he was thinking of small inverterbrates, where very large populations are quite possible. For example, a population of a million million would only require an average density of one per square metre over an area of about a tenth the size of the United States. Ref: J. H. Bennett, ed., Natural Selection, Heredity and Eugenics: Including selected correspondence of R. A. Fisher with Leonard Darwin and others1983 Labels: Burbridge, Population genetics
Thursday, September 04, 2008
Having previously commented on R. A. Fisher's views on epistasis, I have noticed another relevant passage in The Genetical Theory of Natural Selection:
Each successful gene which spreads through the species, must in some measure alter the selective advantage or disadvantage of many other genes. It will thus affect the rates at which these other genes are increasing or decreasing, and so the rate of change of its own selective advantage. The general statistical consequence is that any gene which increases in numbers, whether this increase is due to a selective advantage , an increased mutation rate, or any other cause, such as a succession of favourable seasons, will so react upon the genetic constitution of the species, as to accelerate its increase of selective advantage if this is increasing, or to retard its decrease if it is decreasing. To put the matter in another way, each gene is constantly tending to create genetic situations favourable to its own survival, so that an increase in numbers due to any cause will in turn react favourably upon the selective advantage which it enjoys. The Genetical Theory of Natural Selection, Dover edn., pp.102-3 It would be hard to find a stronger statement of the pervasive role of epistatic fitness in evolution. But I dare say the myth that Fisher 'did not believe in epistasis' will persist. Labels: Burbridge, Population genetics
Monday, September 01, 2008
My series of posts on the work of Sewall Wright is now approaching its (anti?)climax. The next post, on the shifting balance theory, should be the last. The present note deals with a closely related subject. Wright introduced the concept of the 'adaptive landscape' largely in order to illustrate the shifting balance theory. It does however have great interest in its own right, and there is a substantial literature on the concept of adaptive landscapes. [Note 1]
Wright's own treatment of the subject has attracted some controversy following the biography of Wright by William B. Provine. Provine pointed out that Wright used two different interpretations of the 'landscape', which in Provine's view were inconsistent with each other: 'One of Wright's two versions of the fitness surface is unintelligible, and even if one were to escape this problem and put the gene combinations on continuous axes, the two versions would be mathematically wholly incompatible and incommensurable, and there would be no way to transform one into the other' (Provine, p.313). I believe that Provine's criticisms are overstated, but he was right to point out that Wright's concept of the landscape is problematic. This note examines the issues. It is long. Overview The general concept of the adaptive landscape is that the genetic constitution of an individual or a population can be represented by a point in a space of many dimensions. The biological fitness associated with that genetic constitution can then be represented by a measurement along a further dimension. The fitness 'heights' of different genetic constitutions form a quasi-surface. Points or areas of high fitness can be described as 'peaks', points of low fitness as 'pits', 'troughs', etc, and more complex configurations as 'ridges', 'valleys', 'passes', etc. The genetic evolution of a population can be represented by the movement of points around the 'landscape'. Subject to certain provisos, under the influence of natural selection a population will move up the steepest available slope towards areas of higher fitness. If the population reaches a local peak - a point surrounded in all directions by lower ground - evolution will stop until circumstances change in some significant way. Wright believed that in general there will be many local peaks of fitness in the landscape, often differing in height from each other. It is therefore likely that under the influence of natural selection alone, and under constant environmental conditions, a population will get 'stuck' on a peak which is not the highest in the landscape. Evolution would be quicker, and more beneficial to the species, if there were some means of shifting populations away from these suboptimal local peaks. According to the shifting balance theory in its original form, the only way of moving a population from a peak, other than a large and permanent change in environmental conditions, is by genetic drift, which enables a population to cross 'valleys' of relatively low fitness. This is most likely to occur if the species is divided into a large number of small, partially isolated, subpopulations. Some subpopulations will then by chance find themselves on higher peaks of fitness, and their greater reproductive success will result in a net gene flow into other subpopulations, raising the general fitness of the species and enabling evolution to continue. Wright later abandoned his original exclusive emphasis on genetic drift, but this has not always been sufficiently emphasised. I will deal with this more fully in the final post. To consider the 'landscape' in more detail: Sources Wright's first known use of the landscape concept is in a letter of February 3 1931 to R. A. Fisher, quoted in Provine's biography (p.272). Wright's first published account came in a short paper in 1932. Thereafter he discussed the concept in most of his general surveys of population genetics and evolutionary theory. I cannot claim to have read all of Wright's scattered papers, and I have relied heavily on the collection 'Evolution: Selected Papers', (ESP) edited by Provine with Wright's co-operation. Unfortunately, by the operation of Sod's Law, probably the best account of the 'landscape' is not included in ESP (it is in a 1960 Darwin symposium volume edited by Sol Tax). Surprisingly, Wright's huge 4-volume treatise on Evolution and the Genetics of Populations has no systematic treatment of the landscape concept, though various of its component parts are discussed. Finally, a special interest attaches to a paper of 1988, since this came after the publication of Provine's biography. For details see the references. Terminology Wright himself seldom if ever uses the term 'landscape'. In fact, I have not found a single example of it. He does on one occasion (ESP p.625) use the similar term 'topography', but in general he uses two other terms: the field of gene combinations, and the surface of selective values. For convenience I will continue to use the term 'landscape', but anyone searching in Wright's own works should look for 'fields' and 'surfaces', not 'landscapes'. The popularity of the term 'landscape' probably stems from its use in George Gaylord Simpson's Tempo and Mode in Evolution (p.89) and The Major Features of Evolution (p.155), which were more widely read by biologists than Wright's own works. For the same reason, the landscape concept is often given interpretations which derive from Simpson rather than Wright, in which the 'peaks' of the landscape represent either locally optimal phenotypes, or ecological niches. These interpretations are compatible with those of Wright, but not the same as Wright's own landscape, in which the dimensions other than fitness always represent genetic rather than phenotypic variables. The Number of Dimensions Wright's landscape has one dimension for fitness, and others representing the genetic constitution of an individual or a population, which I will call the genetic dimensions. At least one genetic dimension is required for each distinct locus at which more than one allele is present in the population. A position along a genetic dimension represents either the number of copies of an allele (in the case of an individual) or the frequency (proportion) of that allele in the population. Since the number of genes at a locus in an individual must add up to the relevant ploidy (one for a haploid, two for a diploid, etc), and the frequencies of different alleles at a locus in a population must add up to 100%, it is only necessary to specify the number or frequencies of (n - 1) alleles at each locus, since the number or frequency of the n'th allele will then be determined as a residual. It is therefore sufficient to have (n - 1) dimensions for each locus, where n is the number of alleles in the population at that locus. The total number of genetic dimensions is the sum of the (n - 1)'s for all loci. The gene pool of any species probably has at least 1,000 loci at which there are two or more alleles present in the population. The number of genetic dimensions is therefore at least 1,000, and usually much larger. The Axes It might be supposed that the genetic dimensions would be represented diagrammatically by Cartesian axes at right angles to each other (orthogonal axes). For loci with more than two alleles this would however have the disadvantage that the alleles would not be treated symmetrically. For example, with 3 alleles (A, B and C) represented on two orthogonal axes, if one axis represented the balance between A and B, and the other axis the balance between A and C, the balance between B and C could be inferred but would not be directly shown in the diagram. Wright therefore suggests in several places (e.g. Tax p.431-2) that the axes need not be orthogonal, so that for example in the case just mentioned the pairs A-B, A-C, and B-C could be represented by the sides of an equilateral triangle. In practice, Wright usually illustrates his concept with diagrams showing two orthogonal axes for genetic dimensions and one axis (height) for fitness, which on a flat page can be indicated either by perspective or by contours on a map. The Number of Genotypes The number of possible genotypes is vast. With at least 1,000 loci, even if only two positions were possible at each locus, the total number of genotypes representable in the system would be at least 2^1000. Wright himself gives a more generous estimate of 10^1000. Either way, the number is super-astronomical. As Wright points out, it is larger than the number of elementary particles in the universe. It is certainly far greater than the number of individuals in any species. It follows that most of the positions in the genetic 'space' of any actual species will be empty. Even if for most loci a single allele has a high frequency in the population, the genotypes of individuals will be very sparsely scattered over the space. Apart from clones, it is unlikely that two individuals will ever have exactly the same genotype. Genotypes or Frequencies? As Provine showed clearly in his biography (pp.307-17), Wright used two different interpretations of his genetic dimensions. In one interpretation, which I will call the genotype version, a position along a genetic dimension represents the number of alleles of a certain type in an individual genotype. For example, if the dimension represents the allele pair A-a at a diploid locus, a position at one end of the axis would represent the homozygote AA, a position at the other end would represent the homozygote aa, and a position in the middle would represent the heterozygote Aa. [Note 2] The whole genotype of an individual would be represented by a single point in the many-dimensional genotype space, and the allele composition of the individual at a given locus could be 'read off' from the projection of that point onto the relevant axis. The genetic composition of a population could then be represented by a number of points, one for each member of the population, at appropriate positions in the 'space'. In the alternative interpretation, which I will call the frequency version, a position along a genetic dimension represents the proportion of alleles of a certain type in a population. For example, if the dimension represents the allele pair A-a at a diploid locus, a position at one end of the axis would represent fixation (100% frequency) for the allele A, a position at the other end would represent fixation for the allele a, and a position in between would represent an intermediate frequency, e.g. 60% A and 40% a. The entire genetic composition of a population could be represented by a single point at an appropriate position in the 'space'. It must not be inferred that all members of the population would have the genotype represented by this point under the genotype version. In fact, unless most loci are fixed for a single allele, it is extremely unlikely that any individual in the history of the species would have exactly that genotype. There is no doubt that Wright uses both of these interpretations. In his first known account (in the 1931 letter to Fisher) he uses only the frequency version, but in the first published account (1932) he uses only the genotype version. From 1935 onwards his publications most often use the frequency version, but the genotype version is never entirely lost, and the two interpretations may even appear in the same work. (See Note 3 for my own attempt at a chronological listing.) But is there really any inconsistency in the two different interpretations? It is evidently quite possible for a position along an axis to represent either an allele number or an allele frequency, and there is no fundamental reason why the two interpretations should not be used at different times, or even at the same time, provided the differences between the two interpretations are properly noted. There is of course a danger that the use of two different interpretations will lead to confusion, or even to actual error if theorems or generalisations which are valid only for one interpretation are applied to the other one. I am not aware that Wright himself ever falls into definite error, but his explanations are often unclear. According to Provine (p.311) , when he first pointed out the different interpretations to Wright, the latter was somewhat taken aback, and did not realise that he had been switching between them. Wright's 1988 paper, which includes a response to Provine's critique, is surprisingly insouciant about the issue, effectively taking the line: 'Why worry, it's only a diagram.' Provine does have other criticisms, but before discussing these it will be useful to look at the remaining dimension of the landscape, that of fitness. The Dimension of Fitness In view of its importance Wright says surprisingly little about the nature or definition of fitness. In his first presentation of the landscape concept he says only that the entire field of gene combinations can be 'graded with respect to adaptive value under a particular set of conditions' (ESP p.162) . The word 'graded' seems to imply a relative measure of fitness, which is consistent with Wright's general approach and that of many other population geneticists, including Haldane. For most purposes a relative measure is sufficient. Wright does however recognise that an absolute measure, such as Fisher's Malthusian parameter, may be useful or necessary for some purposes, for example in dealing with overlapping generations (Tax, p.433). A more important issue is the question of the relevant 'set of conditions', on which Wright is again disappointingly vague. Clearly the fitness of a given genotype will depend in part on the environment. It appears that Wright intends fitness to be averaged over the usual range of environments in which a species finds itself. But it would be reasonable to object that conditions will be constantly changing, so that there is no such thing as an 'average' environment except at a moment in time. Even at a moment in time the environment will vary in different parts of a species' geographical range. The most important aspect of a species' environment is often not the inorganic factors (climate, etc) but the organic or biotic environment of competitors, food, predators, parasites, and pathogens. These differ fundamentally from the inorganic environment because they are themselves evolving by natural selection, sometimes in response to the species of interest. For example, a new mutation occurring among any of the pathogens affecting a species may dramatically change the fitness of all the genotypes of that species. Wright does in various places recognise that the organic and inorganic environment are liable to change, but he tends to present this as a factor leading to movement of the species around the 'landscape', when it could arguably be seen as invalidating the concept of the landscape altogether. One of the essential features of a landscape, in the ordinary sense, is that it has at least a modicum of persistence through time. For an individual member of a species, the other members of the same species are an important part of its biotic environment. This raises the possibility that the absolute or relative fitness of different genotypes may vary according to the genetic composition of the species population. Notably, this would be the case with various forms of frequency-dependent selection, for example, if pathogens or predators attack the most common variants. I cannot find any discussion of the issue in Wright's early papers. Under the first published (1932) account, which presents only the genotype version, it seems to be assumed that each genotype can be assigned a fitness regardless of gene frequencies. In the first published account of the frequency version (1935), Wright deals mainly with certain special cases, which again seem to be independent of frequency. In two more general presentations (1939 and 1940), I still find no clear statement. Finally, in 1942 (in an article based on a lecture given in September 1941) we find an explicit assumption that 'the relative selective values of these genotypes are independent of their frequencies' (ESP p.472). It may be relevant that in 1941, in a paper referenced in Wright's 1942 article, R. A. Fisher had sharply criticised Wright's 1940 presentation. Whatever the reasons, in later discussions, notably Tax and EGP, Wright gave more attention to the issue of frequency-dependence (see especially Tax pp.443-49). Generally speaking, frequency-dependence can involve either positive or negative feedback, in the first case driving alleles to fixation, and in the second often leading to a balanced polymorphism. If the latter case is common in nature, it would tend to make the landscape concept more difficult to interpret (see further below). Is there a fitness surface? On many occasions Wright refers to the values of the fitness dimension as forming a 'surface'. This would normally imply at least an approximate continuity of values for fitness with respect to changes along the other dimensions. Provine has pointed out that under the genotype version, the fitness values cannot be continuous. The genotype values themselves form a lattice of discrete points, not a surface, so the associated fitness values must likewise be discontinuous. I think this objection is somewhat overstated. First, as a matter of textual detail, Wright seldom uses the term 'surface' when he is referring to the genotype version; in particular, he does not use the term in his first (1932) published account. But on at least one occasion (in 1939, ESP p.318), he does unambiguously refer to a fitness surface with respect to genotypes; also, as Provine points out, even in the 1932 account Wright uses a diagram which seems to imply a continuous surface. Provine's criticism therefore needs to be met, but I think it is not as serious as Provine suggests. It is true that the genotype values form a lattice of points rather than a surface, but it is possible to define a 'distance' between these points by the number of gene substitutions needed to go from one point to another. We can reasonably describe some points as being closer than others. It would then also be reasonable, if not mathematically exact, to say that the associated fitness values approximate to a surface, provided that small differences in distance correspond to small differences in fitness. The real objection, it seems to me, is not that the surface is not strictly continuous, but that the necessary correspondence between fitness and distance does not exist. Genotypes which differ only in a single allele may differ widely in fitness, for example if the heterozygote at a given locus has above-average fitness, whereas the recessive homozygote is lethal. I do not see any basis for an assumption that differences in fitness correspond, even loosely, to the number of genetic differences between two genotypes. I suggest that the following picture is more plausible. A very large part of the 'genotype space' must correspond to zero fitness, since it would involve combinations of rare disadvantageous alleles which are unlikely ever to be combined in reality. Only a small 'corner' of the space is inhabited by actual genotypes. Most of these will have rather similar average fitness, equivalent to producing around two surviving offspring (by sexual reproduction), since, on average, this is what most genotypes actually achieve under their normal circumstances. (If they did not, the population would soon die out.) Among these mediocre genotypes there will be a scattering of super-fit types, and a larger scattering of low-fitness types. The geometrical picture is that most of the landscape would be flat, with uniformly zero fitness, rising gently up to a small inhabited plateau of mediocre fitness, in which there are numerous 'holes' corresponding to genotypes with low fitness (e.g. lethal recessives) compared to their immediate neighbours. [Note 4] There will also be scattered pimples or wrinkles of modest height representing clusters of genotypes containing advantageous genes that are still in the process of selection, and shallow depressions representing mildly disadvantageous genes. But because it contains numerous 'holes' - isolated genotypes or groups of genotypes with fitness much lower than their neighbours - the landscape is not even approximately a continuous surface. If now we turn to the frequency version, there are better grounds for regarding the fitness surface as continuous. In the frequency version each point in the genetic space corresponds to a certain set of allele frequencies at each locus. Provided we make certain assumptions about the mating system and linkage (usually random mating and zero linkage), each array of allele frequencies will be associated with an array of all possible genotypes, each with a definite probability of occurrence. The mean fitness associated with a given point in the frequency space will therefore also be defined. As the point moves around the space, the genotype probabilities will vary continuously, and so will the average fitness, since the value of ab + cd varies continuously if a and c vary continuously, for any fixed values of b and d. It is true that in a finite population the allele frequencies cannot vary with strict mathematical continuity, since they are ultimately fractions with the population size as a denominator, but unless the population size is very small, the fitness surface will approximate to continuity. What is a fitness peak? The idea of a fitness 'peak' is central to Wright's use of the 'landscape' concept. So what exactly is a fitness peak? Characteristically, in introducing the term (in 1932) Wright does not formally define it, and his meaning has to be inferred from what he says about it. This is one issue where it is important to distinguish between the genotype and frequency versions of the landscape. With the genotype version, the definition of a fitness peak is relatively straightforward. If a genotype has higher fitness than any genotype which can be derived from it by substituting another allele at a single site (including e.g. substituting a homozygote for a heterozygote at a given locus), then it may be described as a local fitness peak. So far as I am aware, this is how Wright always uses the term 'peak' under the genotype version. Under the frequency version matters are less clear. We could, of course, stipulate that a set of frequencies is a local peak if any small frequency change at a single locus would reduce the mean fitness of the population. But this would exclude the reasonable possibility that frequencies may change slightly but simultaneously at more than one locus, which might increase mean fitness even though no single-locus change would do so. The natural definition of local fitness peak implied by these considerations is that a set of frequencies is a local fitness peak if no combination of small simultaneous frequency changes, at any number of loci, would increase mean fitness. Geometrically, this is equivalent to stipulating that a local fitness peak is immediately surrounded by downward slopes of fitness in all 'directions' in the genetic space. Probably this intuitive concept could be defined more precisely in terms of the 'principal directions' of differential geometry, but I am not aware that Wright himself ever took this approach. [Note 5] In practice, Wright deals mainly with specific cases where the intuitive meaning of a fitness peak is sufficiently clear. How many peaks? One of Wright's fundamental claims about the landscape is that it has numerous local peaks. Moreover, many of these have a different fitness 'height'. To give some examples (all page references to ESP), he claims that the number of peaks is 'many' (9, 483), 'enormous' (163, 370), 'large' (226), 'inconceivably great' (230), 'multiple' (318), 'innumerable' (348, 554), and even 'virtually infinite' (535). He also insists that many of these peaks will have a different selective value (see the cited or nearby pages for examples). Without these claims, the landscape concept has little interest. The basis of the claims therefore needs to be examined. In his original 1932 presentation Wright used a simple probabilistic argument for the existence of numerous peaks. The number of possible genotypes is vast, so even if only a tiny proportion of them are local optima, the number of local optima would still be very large: 'With something like 10^1000 possibilities it may be taken as certain that there will be an enormous number of widely separated harmonious combinations. The chance that a random combination is as adaptive as those characteristic of the species may be as low as 10^-100 and still leave room for 10^800 separate peaks....(ESP p.163)'. This is a dubious argument. It may be compared to a common argument for the existence of intelligent life elsewhere in the universe. There are around 10,000 billion billion stars in the universe, so even if the proportion of stars with planets supporting intelligent life is tiny - say, 1 in 10,000 billion - there would still be an enormous number of such stars. But consider the following counter-argument. It is plausible that the emergence and survival of intelligent life requires a moderately large number of conditions - say, at least 100 - to be met. It is also plausible that these conditions are largely independent, and individually quite improbable - say, with a probability of only 1 in 100. But with these assumptions, the probability that all of the necessary conditions are met in any given case is less than 1 in 1/100^100. This is vastly less than 1 in 10,000 billion billion, so rather than expecting there to be a large number of stars with planets supporting intelligent life, it would be a miracle if there are any at all. In reality, neither argument goes much further than establishing the bare possibility of the conclusion. Similarly, in the case of selective peaks, the sheer number of possible genotypes is in itself not a strong argument for the existence, rather than the bare possibility, of numerous different peaks. Wright does later present better arguments for the existence of multiple peaks. By far his most common example is that of a quantitative trait controlled by several loci where the selective optimum for the trait is at an intermediate value, i.e. neither the highest nor the lowest that can be produced by the various possible combinations of alleles. In this situation it is likely that the optimum intermediate value of the trait can be produced by different allele combinations. The effect of an allele on fitness (not necessarily on the quantitative trait itself) is epistatic, i.e. dependent on the combination of other genes in the genotype. Which of the relevant alleles are favoured by selection may then depend on the accident of which allele at a locus happens to be most frequent when selection begins, with all other alleles at the locus being driven to extinction. This example is used repeatedly: ESP pp.247, 310, 319, 370, 477, 626, Tax p. 450, EGP vol. 1 pp.59-60. The theoretical possibility of multiple selective peaks in this situation has been generally recognised. As I pointed out in a post on R. A. Fisher and epistasis, it was recognised by Fisher in 1930. It was also noted by J. B. S. Haldane, who is sometimes mentioned by Wright in this context. Indeed, a diagram used repeatedly by Wright to illustrate the point (e.g. ESP pp. 310, 371) looks suspiciously like an adaptation of one used by Haldane (Causes of Evolution, p.107). It should be noted that the example of an intermediate optimal phenotype applies to both the genotype and frequency versions of the landscape concept. Provine has claimed that the two versions are 'mathematically wholly incompatible and incommensurable, and there would be no way to transform one into the other' (Provine, p.313). Like his other criticisms, I think this one is overstated. In at least one important class of cases a local peak under the genotype version will be a local peak under the frequency version as well. This is where the local optimum genotype is homozygous at all loci (or where the organism is haploid). In this case, if all the alleles of the optimum genotype are fixed (i.e. have a frequency of 100%) in the gene pool, all genotypes produced from the gene pool will be identical, and will have the local optimum value. Any change in frequencies (including simultaneous changes in several frequencies) can then only occur by mutations, producing a small proportion of alternative alleles. Assuming random mating and zero linkage, the genotypes produced from the new gene pool will usually differ from the local optimum genotype at no more than a single locus. But by definition these are all less fit than the local optimum, so the change in frequencies will be selected against. Genotypes which differ from the local optimum at more than one locus are indeed possible, and may be fitter than the local optimum, but they will occur so rarely that they can usually be neglected. The frequency array in which all the alleles of a local optimum genotype are fixed in the population will therefore usually be a local peak under the frequency version. If the optimum genotype is not homozygous at all loci, I think Provine is right that there is no easy transition from the genotype version to the frequency version. For any locus that is heterozygous in the local optimum genotype, the heterozygote is most likely to be produced by a 50:50 ratio of the relevant alleles in the population. Let us suppose that the population is fixed for all the homozygous alleles in the optimum genotype, and has a 50:50 ratio for all the heterozygous alleles. Unlike the case where all loci are fixed, this frequency set will produce a multiplicity of genotypes. If there are more than a few heterozygous loci in the optimum genotype, only a small proportion of the genotypes produced from the frequency set will actually have the optimum genotype. (At any heterozygous locus a 50:50 frequency will produce 50% heterozygotes, so if there are n independent heterozygous loci the proportion of genotypes that are heterozygous at all the relevant loci will be (1/2)^n, which rapidly becomes negligible as n increases.) There is no guarantee that this frequency set will be a local fitness optimum (as defined under the frequency version), since this will depend on the fitness of numerous different genotypes, whose mean fitness may well be higher at some other nearby point in the frequency space. It all gets very complicated. If we also take account of frequency-dependent fitness, it is even messier, since there may be no such thing as a local optimum genotype that remains optimal under all frequency arrays. The case of optimum fitness of a trait with an intermediate value does however go some way towards vindicating Wright's confidence in the existence of numerous local peaks. Assuming that there are several such traits which are genetically independent of each other, and of other loci, this may lead to a very large number of local optimum genotypes. With at least two independent optima for each trait, the total number of local optimal genotypes will be at least 2^n, where n is the number of traits. This quickly leads to large numbers: over a thousand for n = 10, over a million for n = 20, over a billion for n = 30, and so on. But there is a snag. Selection for an intermediate value of a trait will, if it is successful, always produce much the same phenotype. For example, if the optimum length of a canine tooth is 1 inch, selection will tend to produce that length of tooth even if different combinations of alleles are involved. In this case there will be multiple peaks in the genetic landscape, but they will all be of much the same 'height' in the fitness dimension. This would take much of the interest out of the concept. Wright recognised this snag at least from 1935 onwards. His answer to the problem was to emphasise that most genes have multiple (pleiotropic) effects, and that the system of peaks relative to one character is therefore not independent of that relative to another (ESP p.230, 320, etc.) In some places Wright seems to imply that the allele frequencies may be fixed at an arbitrary peak by selection for the optimal value of one trait, leaving the effects on some other trait varying and often suboptimal (e.g. ESP p.595, but he is not explicit). But this is doubtful. Suppose for example that an allele combination which determines the length of the canine teeth also affects the incisors. If two such combinations produce the same optimum length of canines, but different lengths of incisors, there will be selective pressure to bring the latter towards its own optimum. In this situation there may well be genes at other loci that are capable of modifying the trait. If necessary, new mutations could be selected (not necessarily absolutely new, but newly advantageous.) It is not clear that significantly different (in fitness) multiple peaks will persist for any trait. In at least one place (Tax p.450) Wright himself may recognise this possibility, but it does not seem to have dented his confidence in the existence of multiple peaks with different fitness. Although the case of intermediate optimum traits is by far the most common reason given by Wright for the existence of multiple peaks, it is not quite the only one. He does occasionally mention the possibility of multiple peaks at a single locus with two or more alleles, if the homozygotes are fitter than the heterozygotes. He also recognises the value of Simpson's concept of phenotypic and ecological peaks, distinguishing two cases: those where different phenotypes give alternative ways of adapting to the same selective conditions, and those where they give ways of adapting to different ecological niches within the same environment (ESP p.555). Conclusions Overall, it seems to me that Wright makes out a plausible case that there are likely to be multiple peaks of fitness, but the arguments are not conclusive. If the environment is changing, as it always is, the landscape itself becomes fluid. And if there is widespread genetic polymorphism and/or frequency-dependence in a population, much of Wright's original formulation is (by his own admission) not directly applicable. Provine's criticisms of the two different versions of the landscape concept seem to me overstated, but he is right to question its usefulness as a heuristic device. If several generations of biologists failed even to notice the existence of the two versions, the metaphor of the landscape can hardly be said to have encouraged clarity of thought. The discussion so far has left some important issues untouched. What are the reasons for expecting a population to 'climb' up a fitness slope? Even if there are many fitness peaks in the landscape, are they all accessible to the population? Will a population get 'stuck' on a peak for any length of time? If so, what circumstances may shift it away from that peak? These questions all go to the heart of the shifting balance theory, so rather than discuss them now I will leave them for my intended note on the shifting balance theory. But before I get there I think it will be useful to cover two supplementary issues which are less directly concerned with Wright's own views. First, what did R. A. Fisher think about all this? And second, apart from Wright's own arguments, what other theoretical or empirical reasons are there for believing in multiple fitness peaks? Note 1: I do not claim to be very familiar with this literature, which is often highly technical and has little to do with Wright's own formulation. See for example the book by Gavrilets and its extensive bibliography. Note 2: Wright himself sometimes uses a notation in which only one of the two alleles at a locus is indicated, so that for example if there are three loci with alleles Aa, Bb, and Cc, the genotype AabbCc could be represented by small letters as abbc, and AABbcc as bcc, and so on. The single genotype in which there are no small letters at all is represented by +. Some of Wright's examples are very difficult to follow if these conventions are not understood. Note 3: 1931 (letter to Fisher): frequency; 1932 (ESP p.163): genotype; 1935 (ESP p.226): frequency; 1937 (ESP p.248): frequency; 1939 (ESP pp.310, 318): both; 1940 (ESP p.347): genotype; 1940 (ESP p.370): frequency; 1941 (ESP p.472): frequency; 1948 (ESP p.535): genotype; 1948 (ESP p543): frequency; 1949 (ESP p. 552): frequency; 1960 (Tax): both; 1977 (ESP p.9): frequency; 1980 (ESP p.626): genotype. Note 4: Terms like 'hole' and 'wrinkle' must be understood as the n-dimensional analogues of these terms in three dimensions. A 'hole' may itself be a figure with many dimensions. Note 5: Even in 3 dimensions, containing 2-dimensional surfaces, differential geometry is a tough subject. For an introduction see Aleksandrov, ed, chapter 7. References Works by Sewall Wright Evolution: Selected Papers (ESP), ed. William B.Provine, 1986 Evolution and the Genetics of Populations (EGP), 4 vols., 1968-1978 'Physiological genetics, ecology of populations, and natural selection', in Evolution After Darwin, vol. 1, ed. Sol Tax, 1960 (Tax) 'Surfaces of selective value revisited', American Naturalist, 131, 1988, 115-23. Other works A. Aleksandrov et al., eds., Mathematics: its content, methods, and meaning, vol. 2, 1963 R. A. Fisher, 'Average excess and average effect of a gene substitution', Annals of Eugenics, 11, 1941, 53-63. Sergey Gavrilets, Fitness Landscapes and the Origin of Species, 2004 J. B. S. Haldane, The Causes of Evolution, 1932 (reprint ed. E. Leigh, 1990) William B. Provine, Sewall Wright and Evolutionary Biology, 1986 G. G. Simpson: Tempo and Mode in Evolution, 1944 (reprint 1984) The Major Features of Evolution, 1953 Labels: Burbridge, Population genetics
Sunday, August 31, 2008
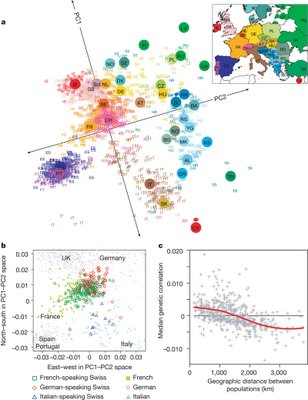 On the heels of the previous paper describing the "genetic map of europe" comes a new paper that makes the same general observation that genetic data contain information about geography. These authors also develop a model that does reasonably well at predicting the country of origin of an individual based on genetics alone. On the heels of the previous paper describing the "genetic map of europe" comes a new paper that makes the same general observation that genetic data contain information about geography. These authors also develop a model that does reasonably well at predicting the country of origin of an individual based on genetics alone. It's worth considering why this is possible. A previous paper by some of these same authors proved that under a simple isolation by distance model, the first two principal components of genetic data are perpendicular in geographic space. So it appears that this basic model is a decent approximation to Europe; further work will likely refine the ways, which are likely to be interesting, that this model doesn't fit the data. The method the authors develop for predicting an individual's country of origin from genetics are only a beginning for this kind of application of genetic data. They note that the SNP chip used in the study only includes common variation, while rare variants are likely to be much more geographically restricted (and thus more informative in this kind of analysis). The limits to the resolution of these sorts of methods are likely to be very fine indeed; the authors note that, even with this panel, they're able to distinguish with some confidence individuals that are from the German, Italian, and French-speaking parts of Switzerland. With full resequencing data, it's likely that even the precise village of origin of an individual will be predictable from genetics alone. Labels: Genetics, Population genetics
Sunday, July 20, 2008
In my recent note on R. A. Fisher and epistasis, I mentioned that Fisher's theory of the evolution of dominance relied on the epistatic effect of 'modifier' genes. On looking again at the chapter in The Genetical Theory of Natural Selection dealing with the evolution of dominance, I see that there is a more general statement of the principle that the effect of a gene depends in part on the genetic background against which it occurs:
The fashion of speaking of a given factor, or gene substitution, as causing a given somatic change, which was prevalent among the earlier geneticists, has largely given way to a realization that the change, although genetically determined, may be influenced or governed either by the environment in which the substitution is examined, or by the other elements in the genetic composition. Cases were fairly early noticed in which a factor, B, produced an effect when a second factor, A, was represented by its recessive gene, but not when the dominant gene was present. Factor A was then said to be epistatic to factor B, or more recently B would be said to be a specific modifier of A. .... These are evidently only particular examples of the more general fact that the visible effect of a gene substitution depends both on the gene substitution itself and on the genetic complex, or organism, in which this gene substitution is made. Labels: Burbridge, Population genetics
Friday, July 18, 2008
My next note on Sewall Wright will cover the exciting subject of the adaptive landscape. As every schoolboy knows, Wright considered epistatic gene interactions very important in determining the 'peaks' of the landscape. A sharp contrast is sometimes drawn between Wright and R. A. Fisher in this respect. For example:
What is said here about Wright seems broadly correct, but what is said about Fisher is seriously misleading. Before continuing with my notes on Wright, I will therefore try to clarify Fisher's views on epistasis.[Note: due to formatting problems, italics and other refinements may be omitted.] First, it is necessary to say something about the meaning of epistasis. The term 'epistasis' itself seems to have emerged around 1917. The first use cited in the OED is from the index to the 1917 volume of the journal Genetics. Around the same time Fisher, in writing his 1918 paper on the Correlation of Relatives, coined the term 'epistacy', but this never caught on. Both terms were derived from the adjective 'epistatic'. Like much of the terminology of genetics (including the word 'genetics' itself) this was coined by William Bateson, in 1907. Bateson used it with a relatively limited meaning to describe cases where a gene at one locus masked or suppressed the action of genes at another locus. For example, genes at one locus might affect the pigmentation of an animal's fur, but a gene at another locus might suppress the production of pigment entirely, causing albinism. In this case the trait of albinism (or the gene producing it) would be called epistatic (literally 'standing over'), while the traits that were masked would be called 'hypostatic' (literally 'standing under'). This limited usage of 'epistatic' is still sometimes found in medical genetics, but in evolutionary genetics a wider usage is more common. In the wider usage, epistasis is any kind of interaction between genes at different loci. Of course, many traits are affected by genes at more than one locus, but this does not necessarily imply interaction. The meaning of 'interaction' is that the genes at different loci do not act independently. For qualitative traits, the usual test of this is that the traits of the offspring do not show the expected Mendelian ratios (which is how epistasis in Bateson's sense was originally discovered). For quantitative traits, the usual criterion is that the value of the trait is not simply the sum of the values attributable to the individual genes concerned. If it is simply the sum, the genes are often said to have a purely 'additive' effect. If not, the trait either shows dominance (if the interaction is between genes at the same locus) or epistasis (if at different loci). Assuming that epistasis can be identified (which in practice is often very difficult for small effects), it may be asked how the effects of epistatic interaction on a quantitative trait can be measured. One answer to this would be to decide that where interaction is involved, the entire effect of the interacting genes should be counted as epistatic. But this seems unreasonable if the same genes would still have some effect even if there were no interaction. An ideal solution might be to find cases in which the genes concerned are not involved in any epistatic relations, and measure their effect in these circumstances, then subtract this from the effect in the case of epistasis. But if epistasis is a widespread phenomenon, it would be difficult to find these non-epistatic cases, since most genes would show some effects of interaction. In any event, a different approach is generally taken. The usual approach to measuring the effects of epistasis is roughly as follows. Each gene is assigned a value (the 'average effect' of the gene) based on the average value for the trait concerned among those members of the population who carry that gene, expressed as a deviation from the population mean. Each genotype (gene combination) is then assigned a value based simply on the sum of these average values. This is called the 'breeding value', since it is the part of the genetic makeup of the individual which enables the traits of its offspring to be predicted for breeding purposes. These breeding values will have a certain variance, relative to the population mean, usually called the additive genetic variance. The actual observed values will have a greater variance than this, due to the effects of environment, dominance, epistasis, and various other complications. The portion of the observed variance attributable to epistasis is estimated after the effects of environment and dominance have been subtracted. Genes with epistatic effects are not excluded from the analysis, and they may contribute to both additive and (in a more complicated way) to dominance variance as well as to the specific epistatic or 'genetic interaction' variance. All this is explained more fully, and no doubt more clearly, in Falconer. For a simple worked example of my own see Note 1. The standard terminology is unfortunate. It cannot be stressed too strongly that 'additive' variance is not the same as the variance due to genes with purely additive effects. The additive variance takes account of the average effects of all genes, including those that may show strong dominance or epistasis. These average effects depend in part on the gene frequencies present in the population in question, and assume that all possible genotypes occur in the proportions expected under a given system of mating (usually assumed to be random). Part of the average effect is therefore due to the effects of gene interactions. Conversely, the so-called 'epistatic variance' covers only a part - usually the minority - of the effects that might intuitively be ascribed to interaction. Enthusiasts for epistasis (as in the volume already cited) sometimes complain that the standard method of apportioning variance tends to understate the effects of epistasis, and makes it difficult to detect. For example, James Cheverud comments that 'most tests for epistasis rely on the epistatic variance alone and ignore its contribution to additive and dominance variance' (p.65) and Edmund Brodie says that 'under a wide range of allele frequencies and strengths of interaction, the majority of variance produced by gene interaction is actually additive' (p.10). It would be possible in principle to use alternative measures which assign more of the observed variance to epistasis. But the standard method does have the advantage that it is possible to estimate the additive variance from the observed correlation between parents and offspring, and conversely to estimate the value of offspring from that of parents. This is particularly important if we wish to predict the effects of natural or artificial selection. Whatever we call it, the 'additive' variance is a useful concept and is not going to go away. It is also desirable to distinguish between epistasis for fitness and for other traits of the organism. Fitness itself (whether measured simply by number of offspring or otherwise) shows epistasis if the effects on fitness of genes at different loci are not purely additive. If fitness is measured in relation to some particular trait, the fitness may show epistasis even if the trait as such does not. (And presumably vice versa, though I cannot think of a plausible scenario for this.) For example, a trait such as body size might be influenced by several genes acting purely additively in their effects on body size, but epistatically in their effect on fitness. This will often be the case if fitness is highest for some intermediate value of the trait. The fitness effects of genes tending to raise (or lower) the value of the trait will then depend crucially on the other genes they happen to be combined with. In the simplest case, if there are two haploid loci, with alleles H and L (for High and Low) at one locus, and h and l at the other, the combinations Hl and hL, which give intermediate size, may be favoured by selection, while the combinations Hh and Ll, which give high and low size respectively, are selected against. In this case the fitness is epistatic even though the direct effect of the genes on the phenotype is additive. After all these preliminaries, I turn to discuss what Fisher actually said about epistasis. Correlation of relatives As already mentioned, Fisher's great 1918 paper on the 'Correlation of Relatives' proposed the term 'epistacy' to allow for the interaction of genes at different loci, and devised the standard method for apportioning variance. Fisher introduces his definition of 'epistacy' as follows: 'There is in dominance a certain latency. We may say that the somatic [phenotypic] effects of identical genetic changes are not additive, and for this reason the genetic similarity of relations is partly obscured in the statistical aggregate [see Note 2]. A similar deviation from the addition of superimposed effects may occur between different Mendelian factors [genes at different loci]. We may use the term Epistacy to describe such deviation, which although potentially more complicated, has similar statistical effects to dominance. If the two sexes are considered as Mendelian alternatives, the fact that other Mendelian factors affect them to different extents may be regarded as an example of epistacy. The contributions of imperfectly additive genetic factors divide themselves for statistical purposes into two parts: an additive part which reflects the genetic nature without distortion, and gives rise to the correlations which one obtains, and a residue which acts in much the same way as an arbitrary error introduced into the measurements. ' (p.404) Note that Fisher says here quite explicitly that part of the contribution of 'imperfectly additive' genes is itself additive, or as we would say, falls within the additive variance. Fisher does not say a great deal more about 'epistacy' in this paper (but see p.408-9 for the mathematical treatment of epistatic variance), and one of the contributors to the volume cited earlier claims that in his 1918 paper Fisher 'dismissed gene interactions as being of only minor importance in the evolutionary process, analogous to nonheritable modifications of the phenotype' (p.125). This goes beyond anything Fisher says. What he does say is that 'Throughout this work it has been necessary not to introduce any avoidable complications, and for this reason the possibilities of Epistacy have only been touched upon...' (p.432). For Fisher's specific purpose in this paper, which was to explain the correlation between relatives on Mendelian principles, and not to discuss evolutionary theory in general, his brief treatment of 'epistacy' seems sufficient. Fisher finds that with his methods the existing data on the correlation of relatives (mainly the data of Karl Pearson on humans) can be explained satisfactorily by additive variance, dominance, and assortative mating, without much influence of other factors, which by implication include epistatic variance. Fisher is more explicit about this in his 1922 paper on the Dominance Ratio, where he says that 'special causes, such as epistacy, may produce departures [from the expected correlations], which may in general be expected to be very small from the general simplicity of the results'. But before interpreting this as a general pronouncement on the insignificant role of epistasis in evolution, we should note that (a) the additive variance includes much of the effect of 'epistatic' genes, and (b), the discussion was concerned with ordinary traits such as height, and not with fitness. As emphasised earlier, there may be epistasis for fitness even if the underlying traits are purely additive. The evolution of dominance One of Fisher's best-known, and most controversial, theories is that of the evolution of dominance. Noting that harmful mutations are usually (though not always), recessive in their effects, Fisher sought to explain this by the action of modifier genes at other loci, which would be gradually selected to minimise the harmful effects of common recurring mutations by making them recessive. The theory has not been generally accepted, and Wright in particular opposed it, mainly on the grounds that the selective advantage of modifier genes would be so weak that it would usually be overpowered by their other, more direct, effects. Regardless of whether Fisher was right or wrong on this issue, the point to note here is that his theory depends entirely on epistatic effects! In this respect, at least, Fisher was more enthusiastic about epistasis than Wright himself. Mimicry A whole chapter of the Genetical Theory of Natural Selection is concerned with Mimicry. In discussing the underlying genetics of mimicry, Fisher emphasises the role of modifier genes, including those that act as 'switches' for other genes. For example, discussing the 'hooded' gene in rats, he says 'The gene, then, may be taken to be uninfluenced by selection, but its external effect may be influenced, apparently to any extent, by means of the selection of modifying factors' (p.185). And in discussing another case he goes on to say 'The gradual evolution of such mimetic resemblances is just what we should expect if the modifying factors, which always seem to be available in abundance, were subjected to the selection of birds or other predators' (p.185). While modifiers might in principle be purely additive in effect, they are more likely to be epistatic. This is presumably always the case with 'switch' genes. Sex Chapter 6 of GTNS deals with a variety of issues concerning sex, sexual selection, sex-limited traits, and speciation. Some of these could well involve epistasis - indeed, 'sex-limited' traits (those which are only manifested in one sex) do so almost by definition, if sex is genetically determined. (As mentioned in Fisher's paper on 'Correlation of Relatives', quoted above, differences between the sexes can be regarded as a case of 'epistacy'.) However, I find only one definite reference in the chapter to epistatic effects. In his discussion of speciation, Fisher points out that the adaptiveness of genes will vary in the different parts of a species's range, and says that 'In addition to those genes which are selected differentially by the contrasted environments, we must moreover add those, the selective advantage or disadvantage of which is conditioned by the genotype in which they occur, and which will therefore possess differential survival value, owing not directly to the contrast in environments, but indirectly to the genotypic contrast which these environments induce' (p.141). A difference in the selective advantage of a gene according to the genotypic background implies epistatic fitness. What Fisher is describing here is actually what is often called a 'co-adapted gene complex', much beloved of Wrightians. The Fundamental Theorem of Natural Selection The Fundamental Theorem of Natural Selection states that 'The rate of increase in fitness of any organism at any time is equal to its genetic variance in fitness at that time' (GTNS p.37). The FTNS is notoriously difficult to interpret, and I do not intend to say much about it here. It is however now generally accepted, following the interpretations by George Price and A. W. F. Edwards, that when Fisher refers to 'genetic variance' he means the 'additive' genetic variance. The additive variance takes account of the average effect of genes in all the various environmental circumstances and genetic combinations in which they are found, in the proportions to be expected under a given system of mating. (See expecially p.31 of GTNS, where Fisher defines 'average excess' and 'average effect'.) It therefore incorporates the effects of dominance and epistasis to the extent that these contribute to the additive value of the genes. There is no reason at all to suppose that genes with epistatic effects are excluded from the FTNS. What is excluded is only that part of the total variance that is not covered by the contribution of those genes to additive variance. This can be justified on the grounds that the non-additive variance does not predictably change gene frequencies in the next generation and therefore has little effect on evolution. As Cheverud admits, 'the rate of evolution is determined by the additive genic [sic] variance alone' (p.65). Selection at two loci Before 1930 neither Fisher nor Wright had treated selection at more than one locus. As so often, the pioneer of the subject was J. B. S. Haldane, in 1926. In 1930 Fisher did however give the subject a short section in Chapter 5 of GTNS, under the heading 'Equilibrium involving two factors'. (This chapter is one of several that appear to be invisible to some readers.) The interesting situation, as Fisher recognises, is where two different combinations of alleles (e.g. AB and ab) are both favoured by selection, while the same genes are disadvantageous in other possible combinations (e.g. Ab and aB). Fitness in this case is therefore clearly epistatic. In his chapter summary Fisher says that stable equilibria may be established, but he is rather vague about the conditions for stability. But his main point is that there will be selection in favour of closer linkage between favourable gene combinations on the same chromosomes, and it is therefore a puzzle why recombination is as frequent as it is. I think this remains a problem. In any event, it is a case where Fisher clearly recognised the role of epistasis. Selection of metrical characters One of the most intriguing, but difficult, sections of GTNS is the one (also in the 'invisible' Chapter 5) on 'Simple metrical characters'. (I sometimes wonder if Fisher's use of the word 'simple' was a sly joke.) The case of interest is where a quantitative character, such as the size of a tooth, is regulated by genes at more than one locus, and subject to stabilising selection in favour of an intermediate size. Egbert Leigh has described this (in his 'Afterword' to the 1990 reprint of Haldane's 'The Causes of Evolution') as 'a topic still replete with mysteries and surprises'. Fisher's account is even more tangled than most, because he attempts to explain simultaneously selection of the metrical trait itself and selection for dominance of the genes controlling it. I cannot pretend to understand everything he says on the subject, but what is clear for the present purpose is that fitness in this case is epistatic, and that there may be more than one outcome of selection, depending on the initial frequencies of the genes concerned: 'the conditions of equilibrium are always unstable. Whichever gene is at less than its equilibrium frequency will tend to be further diminished by selection' (p.121). This is precisely the situation which Wright often emphasised as leading to alternative 'selective peaks'. But unlike Wright, Fisher did not believe a species was likely to get 'stuck' permanently on a selective peak (not that Fisher had much time for the adaptive landscape anyway). Fisher believed that following any change in the optimum phenotypic value due to environmental change there would be sufficient genetic variation (in a large population) for selection to shift organisms quickly towards the new optimum. His confidence in this was based mainly on the results of artificial selection, as he referred to 'the extreme rapidity with which such measurements are modified when selection is directed to this end' (p.119). The effects of such changes on gene frequencies might be lasting, even if the initiating circumstances were temporary. In Fisher's analogy, which may be more illuminating to physicists than to me, 'the system resembles one in which a tensile force is capable of producing both elastic and permanent strain, and in which the permanent deformations always tend to relieve the elastic forces which are set up' (p. 125). This section of GTNS raises a rather intriguing historical possibility. As Provine has noted in his biography of Wright (Provine p.285-6), there was an unexplained change in Wright's account of the 'shifting balance' theory between his exposition in 'Evolution in Mendelian Populations' (1931), and his next major account in 1932. In 1931 he had asserted that temporary changes in the environment would only have temporary effects on the gene pool, being essentially reversible. Hence his emphasis on genetic drift in small subpopulations, as the only possible means of shifting from one peak to another. In 1932, on the other hand, he accepted that environmental changes could also shift a population from one stable peak to another, so that their effects might be lasting even after the change in environment had reversed. Unfortunately Wright did not explain the reasons for his change of mind, nor did he draw attention to the change, which is really very important, since it greatly weakens Wright's argument for the importance of genetic drift in small local subpopulations. Provine speculates, plausibly enough, that Wright's correspondence with Fisher, his reading of GTNS, and Fisher's own published review of 'Evolution in Mendelian Populations', had something to do with the change. My own suggestion, to build on this, is that Fisher's discussion of metrical characters in Chapter 5 of GTNS was a particular influence. But I have no direct evidence of this, so it will probably remain a mere speculation. Conclusions The main purpose of this note has been to identify and document what R. A. Fisher himself, as opposed to the straw man 'Fisher', actually said and believed about epistasis. Readers will be able to draw their own conclusions, but I will briefly indicate my own. a) Fisher did not deny the existence of epistasis, in the broad sense, and in some specific cases - including the evolution of dominance, selection at two loci, and quantitative (metrical) traits under stabilising selection - he gave it an important role. b) Fisher agreed with Wright (and Haldane) that in some circumstances, including stabilising selection, there could be more than one outcome of selection in terms of the resulting gene frequencies. Unlike Wright (in 1931), but like Wright (in 1932), he believed that temporary environmental change could shift a population durably from one equilibrium set of gene frequencies to another. Fisher's treatment of the problem in GTNS may have influenced Wright's unexplained volte-face on this important issue. c) Fisher did not believe populations were likely to get stuck on a local peak in the selective landscape, but this was not because he did not believe in epistatic effects, but because he did not believe in the validity of the selective landscape concept at all. I will probably say more about Fisher's thinking on this in another post. d) Fisher's general concept of evolutionary change, as expressed in the Fundamental Theorem of Natural Selection, does not exclude epistatic effects. The FTNS takes account of epistasis (and dominance) precisely to the extent that they do affect the rate of evolutionary change. The FTNS is neutral with respect to the importance of epistasis: whether it is important or unimportant cannot be inferred from the theorem, which takes account of additive variance in fitness whatever its source. Unfortunately much confusion has arisen about the meaning of 'additive' and 'epistatic' variance. If it is not understood that 'additive' variance includes much of the effect of epistatic genes, while 'epistatic' variance excludes much of that effect, the scope of the FTNS will be seriously misconstrued. It would be better to call additive variance something like 'heritable variance', while the non-additive effects of dominance and epistasis are clearly labelled in such a way as to make it clear that they are only part of the total effect of gene interactions. e) Unlike Wright, Fisher did not, at least in his published works, put any emphasis on epistasis as a major factor in evolution. It is necessary to read GTNS quite carefully (or at least to look at all the chapters!) to find the references I have gathered together here. It is an empirical matter whether epistasis plays the central role that Wright gave it. Or it might have an important role that neither Wright nor Fisher had thought of, as suggested in Kondrashov's theory of sex. I have not dealt here with another aspect of Fisher's views, namely his rejection of the importance in evolution of large single mutations. I have no doubt that Fisher believed that evolution occurred mainly through the selection of a large number of genes with individually small effects. I have not discussed this because (a) it was not a point of disagreement between Fisher and Wright, and (b) it does not seem relevant to the issue of epistasis. As far as I can see, large mutations are no more or less likely to have epistatic effects than small ones. Addendum After writing the above, I came across a further reference to epistasis in Fisher's correspondence. Writing to Leonard Darwin in 1928, Fisher said 'I am inclining to the idea that the main work of evolution lies in the discovery by trial of perhaps rare combinations of its existing variants, which work better than the commoner combinations. A slight increase in the number of individuals bearing such a favourable combination will then set up selection in favour of all the genes in the combination, with marked evolutionary results. Many of these genes would have been previously rare mutant types (not necessarily rare mutations) unfavourable to survival. I think of the species not as dragged along laboriously by selection like a barge in treacle, but as responding extremely sensitively whenever a perceptible selective difference is established. All simple characters, like body size, must be always very near the optimum, so much so that the average body sizes of two alternative genes must be balanced on either side of the optimum, selection always tending to eliminate the rarer because it is further from the optimum...' (Correspondence p.88). In his Introduction to the correspondence, J. H. Bennett draws attention to this letter, and remarks that 'It is interesting, and perhaps needs emphasizing, that both Fisher and Wright considered systems of interacting genes to be of critical importance in evolution. A fundamental difference in their views of the evolutionary process concerned the means by which interaction systems could be exploited' (p.47) While I agree with Bennett that Fisher took some account of 'interaction systems' , in other words epistasis in the broad sense, this letter of 1928 seems a good deal more positive on the subject than anything I have noticed in his published works. I take this opportunity to say that Bennett's Introduction is one of the most useful things yet written on Fisher's work and ideas, and deserves repeated reading. Note 1 Consider the simplest case of a haploid organism with a quantitative trait determined by genes at two loci. I assume complete genetic determination. Let the alleles in the population be A and a at one locus, and B and b at the other, each with a frequency of 50% in the population. Under random mating the four genotypes AB, Ab, aB and ab will therefore all have the frequency 25%. (In a diploid there would be nine genotypes to consider, and the possible complication of dominance, which is why I have chosen the haploid case.) Let us suppose that the measurements of the trait for the four genotypes are as follows, where c and d are any numerical values: AB........c + d Ab........c aB........c ab.........c I have chosen these values to dramatise the situation. Intuitively, one would say that all of the variation in the trait was due to the epistatic interaction of A and B, since all other genotypes than AB have the identical value c. So let us see how the variance comes out under the standard method. The mean value of the trait in the population is evidently .75c + .25(c + d) = c + .25d. The mean values for each gene considered separately, measured by the average value of the individuals who possess that gene, are: A........ .5(c + d) + .5c = c + .5d a......... c B........ .5(c + d) + .5c = c + .5d b........ c Expressed as deviations from the population mean, c + .25d, these values come out as: A........ + .25d a......... - .25d B........ + .25d b........ - .25d These are known as the 'average effects' of the genes in question. The so-called 'breeding value' of a genotype is simply the sum of the average effects of its component genes, so for the four genotypes we have the breeding values: AB.......... + .5d Ab.......... 0 aB.......... 0 ab.......... - .5d It may be noted that the combination ab has a substantial (negative) breeding value, even though there is, intuitively, no interaction between a and b. This reflects the fact that the interaction of A and B pulls up the population mean, and therefore affects the deviation values of other alleles and genotypes. The combination ab falls as far below the resulting mean as the combination AB rises above it. The symmetry is of course a consequence of the symmetry of the chosen assumptions about gene frequencies, etc. The breeding values are already deviations from the population mean, so for the variance of breeding values (the so-called additive genetic variance) we have: .25(.5d)^2 + .25(0)^2 + .25(0)^2 + .25(.5d)^2 = .125d^2. It is already apparent that although the variance is intuitively entirely due to epistasis, the 'additive' variance is not zero. For comparison, we can measure the total variance of the values of the genotypes. The deviation values are as follows: AB.......... c + d - (c + .25d) = .75d Ab, aB, and ab.......... c - (c + .25d) = - .25d Taking account of the proportions of the genotypes in the population we therefore have the variance of genotypic values as follows: .25(.75d)^2 + .75(- .25d)^2 = .1875d^2 Subtracting the 'additive' variance from the total genotypic variance we find only .0625d^2 left for the 'epistatic' variance. So even where we have rigged the example to give a strong influence to epistasis, 2/3 of the resulting variance is 'additive', and only 1/3 'epistatic'! Note 2: I think that by 'genetic changes' in this sentence Fisher means not just mutations, but any gene substitution, such as may occur through the normal processes of sexual reproduction. So, for example, if at a single locus the combination aa is replaced by the combination Aa, there will be a certain measurable effect of the change. If the effect of substituting two As is twice the effect of substituting just one A, the effect is additive. Otherwise the locus shows some degree of dominance. References: D. S. Falconer: Introduction to Quantitative Genetics, 3rd. edn., 1989 R. A Fisher: The Genetical Theory of Natural Selection, 1930. I have given page references to the revised Dover edition of 1958, but the quoted passages are all unchanged from the first edition. For scholarly purposes the best edition is now the Variorum edition of 1999, edited by Henry Bennett. Fisher's papers are cited from the online copies available from the archives at Adelaide (see link on sidebar) Natural Selection, Heredity and Eugenics: Including selected correspondence of R. A. Fisher with Leonard Darwin and others, edited by J. H. Bennett (1983). Much of the correspondence is also available online from the archives at Adelaide. Epistasis and the Evolutionary Process, ed. J. B. Wolf, E. D. Brodie, and M. J. Wade. 2000 William B. Provine: Sewall Wright and Evolutionary Biology, 1986. (Paperback edn. 1989) Labels: Burbridge, Population genetics
Thursday, July 10, 2008
In Scientific American. If you've been following this site, it's old hat to you, but still.
Via ALDaily. Labels: Population genetics
Thursday, July 03, 2008
Continuing my series of notes on Sewall Wright's population genetics, I come to the subject of migration. This is important in understanding the differences between Wright and R. A. Fisher on the role of genetic drift in evolution. Fisher and Wright both agreed that genetic drift would be too weak a process to be of evolutionary significance in large populations (above, say, 10,000 in effective size) . [Note 1] Equally, they agreed that it would be important in small populations, provided these remained sufficiently isolated over sufficiently long periods of time. Their disagreement was over the probability that the necessary degree of isolation would occur. This depends largely on the rate of migration between populations.
Fisher's views on the subject can be pieced together from scattered remarks, as I attempted here. It seems that from an early stage - at least from his 1921 review of the 'Hagedoorn Effect' - Fisher regarded small isolated populations as unimportant in evolution. If they stayed isolated for long, they would go extinct from occasional adverse conditions (epidemic disease, drought, etc). If they did not stay isolated, the flow of migrants from outside (whether in a steady small trickle, or occasional larger floods) would be sufficient to prevent their gene frequencies from drifting far from those of the general population of their species. But so far as I know, Fisher never made any formal quantitative estimate of the amount of migration necessary to offset genetic drift. Sewall Wright, on the other hand, did make such estimates, and developed them in published works from 1931 onwards. It is known that a first draft of Wright's major 1931 paper on 'Evolution in Mendelian Populations') was written as long ago as 1925. In this he already took the view that genetic drift in small semi-isolated populations was an important evolutionary factor. This might suggest that by that time he had already considered the role of migration in depth. The draft of 1925 has not survived (Provine p. 237), but it seems that in fact it did not yet contain a detailed treatment of migration. The evidence for this is from Wright's correspondence with Fisher in 1929. Wright told Fisher that 'since I wrote [in August 1929, sending a copy of his draft] I have been trying to get a clearer idea of the effect of diffusion [i.e. migration] and I see, at least, that isolation in districts must be much more nearly complete than I realized at first, to permit random fixation of strains' [Provine p.256]. This conclusion is presented more formally in 'Evolution in Mendelian Populations' (at ESP pp.127-9). Here Wright develops an equation for the distribution of gene frequencies which incorporates a term for m, the rate of migration into a small semi-isolated population from a larger population with different gene frequencies. The exact meaning of this equation is difficult to interpret [see Note 2], but Wright's own conclusion is that 'Where m [the migration rate] is less than 1/2N [with N being the effective size of the receiving population] there is a tendency toward chance fixation of one or the other allelomorph [i.e. one of the alleles at a locus where there are two alleles in the population]. Greater migration prevents such fixation. How little interchange appears necessary to hold a large population together may be seen from the consideration that m = 1/2N means an interchange of only one individual every other generation, regardless of the size of the subgroup'. This conclusion has been widely restated in the population genetics literature. Unfortunately I do not know of any clear and mathematically elementary proof. (John Maynard Smith [p. 158-60] presents a proof using only basic algebra, but it combines the treatment of migration and mutation, and involves various simplifying assumptions and approximations. There are also some confusing misprints or slips of the pen.) It may be surprising that the rate of migration sufficient to prevent populations drifting apart can be stated as a constant number of migrants, regardless of the size of the population. D. S. Falconer comments that 'This conclusion, which may at first seem paradoxical, may be understood by noting that a smaller population needs a higher rate of immigration than a larger one to be held at the same state of dispersion' [Falconer p.79]. We may put this point slightly more formally by noting that the effect of migration in offsetting drift may be expected to be proportional to the rate of migration. The rate can be expressed as n/N, where n is the number of migrants and N is the effective size of the receiving population. Since the effect of genetic drift has previously been shown to be proportional to 1/2N, we can therefore expect the migration rate required to neutralise drift to be n/N = k/2N, where k is some constant factor of proportionality. But it follows that in equilibrium we will have n = k/2, where k is a constant. Of course, this does not tell us the size of k, but it is plausible that it is of the order of 1, as is proved by Wright and others using more rigorous methods. The conclusion that only around 1 migrant every other generation is sufficient to prevent sub-populations drifting apart might seem fatal to Wright's belief in the importance of genetic drift. As shown in his correspondence with Fisher, Wright does initially seem to have had his confidence shaken. But Wright (like Fisher) was not one to give up a cherished theory without a struggle. Immediately following the quoted passage from 'Evolution in Mendelian Populations', Wright continues: 'However, this estimate must be qualified by the consideration that the effective N [the population size] of the formula is in general much smaller than the actual size of the population or even than the breeding stock, and by the further consideration that qm ['m' is a subscript, indicating the frequency of the allele among the migrants] of the formula refers to the gene frequency of actual migrants and that a further factor must be included if qm is to refer to the species as a whole. Taking both of these into account, it would appear that an interchange of the order of thousands of individuals per generation between neighboring subgroups of a widely distributed species might well be insufficient to prevent a considerable random drifting apart in their genetic compositions' (ESP p.128). Wright's first point, that effective N may be lower than the apparent size of the population, is either confused or confusing, since Wright has just proved that N, the effective size of the receiving population, is irrelevant to the number of immigrants required to neutralise drift. Perhaps Wright is thinking of the effective number of migrants, rather than of the receiving population, in which case the number who succeed in contributing to the gene pool may indeed be less than the total number. The second point is valid, but not well explained. Wright's formula contains a term mqm (with the second m a subscript), where qm is the frequency of the relevant allele among the migrants. But the underlying assumption is that this is the same as in the species generally. Wright's point (made more explicitly in later papers) is that the allele frequencies in neighbouring populations are likely to be more similar than in the species generally, so that mqm will actually be less than is assumed in the derivation of the result. To adjust for this we might stipulate that the 'effective' number of migrants is smaller than the actual number, even of those who successfully breed, just as the 'effective' population size may be smaller than the actual size. This approach is clearer in later papers, for example at ESP p.236: 'Cross breeding is, however, most likely to be with neighboring populations which differ but little in value of q. In this case the coefficient m is only a small fraction of the actual amount of change [i.e. the actual observed rate of migration]'. With this adjustment of mqm, the number of actual migrants required to neutralise drift might indeed be many more than 1 per generation. This is valid as far at it goes, but it depends on the assumption that allele frequencies in neighbouring populations are likely to be relatively similar. This is perfectly plausible, but only because we tacitly assume that migration between neighbouring subpopulations is, or recently has been, sufficient to offset genetic drift. Wright therefore seems perilously close to sawing off the branch he is sitting on. Certainly, if the allele frequencies do drift 'considerably' apart (to use Wright's word in 'Evolution in Mendelian Populations'), the assumption of similar frequencies ceases to apply, and we can no longer rely on it. A further consideration is that on an evolutionary time scale (i.e. hundreds or thousands of generations) occasional larger influxes of migrants are almost bound to occur, and undo all the slow work of genetic drift. Even if an allele is lost or fixed in a subpopulation, it can be reintroduced at any time by migration from outside, so long as it persists somewhere in the species. Wright continued to study the effect of migration after 1931, with his fullest treatment in the paper 'Isolation by Distance' in 1943 (ESP pp.401-425). Here Wright examines three different models for migration: the Island Model, in which migrants are derived at random from a number of semi-isolated subpopulations of the species, and therefore on average have the gene frequencies of the species as a whole; isolation by distance in a two-dimensional continuum, where the probability of cross-breeding is proportional to the distance between the birthplaces of the breeding individuals; and isolation by distance in a linear range such as a river-bank. Wright's conclusions from the Island Model are not very different from those in his 1931 paper based on the cruder assumption of random migration throughout the species. The conclusions from two-dimensional isolation by distance are only slightly more favourable. As he summarises it in 1943: 'It is apparent that there is a great deal of local differentiation if the random breeding unit is as small as 10, even within a territory the diameter of which is only ten times that of the unit. If the unit has an effective size of 100, differentiation becomes important only at much greater relative distances. If the effective size is 1000, there is only slight differentiation at enormous distances. If it is as large as 10,000 the situation is substantially the same as if there were panmixia [random mating] throughout any conceivable range' (ESP p.411). Only for the more special linear-range model is there substantial differentiation due to drift in populations of moderate size. Wright's theoretical conclusions might seem to imply that genetic drift in subpopulations would seldom be a major factor in evolution. It seems to require rather special circumstances to be effective: either very small populations, populations sparsely scattered with long distances between them, populations with a narrow linear range, or organisms that are very immobile at all stages of their life cycle. Wright nevertheless continued to insist throughout his career that drift in subpopulations was an important, if not essential, feature of evolution. The uncharitable view of this would be that Wright was simply stubborn. Having taken up his position on the importance of this factor, before having considered in depth the effects of migration, he was determined to defend it. come what may. (There would be a parallel here with the equally stubborn position of Fisher on the evolution of dominance.) A more charitable view would be that Wright was trying to find an explanation of something that was generally accepted by biologists when he began his career: namely, that the observable differences between subspecies, and even between species, are usually selectively neutral. Wright himself stresses this point in 'Evolution in Mendelian Populations': 'It appears, however, that the actual differences among natural geographical races and subspecies are to a large extent of the nonadaptive sort expected from random drifting apart. An interesting example, apparently nonadaptive, is the racial distribution of the 3 allelomorphs which determine human blood groups' (ESP p.128). In the years and decades following 'Evolution in Mendelian Populations', the opinion of biologists turned away from the consensus view in 1931 (really no more than a superficial assumption) that subspecific differences are selectively neutral. Much of the relevant research was carried out by the students and collaborators of Wright and Fisher themselves, notably E. B. Ford in England and Theodosius Dobzhansky in the USA. The general outcome was that even apparently minor subspecific differences often had some selective value. Human blood groups, for example, were found to be correlated with resistance to different diseases, though it remains unclear whether all such differences have a selective basis. The importance of genetic drift in subpopulations is of course an empirical matter. It is quite possible that some species are 'Wrightian' and some are 'Fisherian' in this respect. The observed amount of genetic diversity between subpopulations is usually quite modest (Maynard Smith p.160-161], suggesting that migration between them is usually sufficient to prevent them drifting far apart . There are theoretical reasons for expecting that 'Fisherian' species would be in a majority. Most species have adaptations for dispersal at some stage of their life. Plants, for example, have adaptations for spreading their seeds. Among animals, the juveniles of one or both sexes often disperse from their region of birth to find mates or territories. With a few exceptions, organisms that just stick to one spot are doomed to extinction within a fairly short period of evolutionary time, since the conditions of life seldom stay fixed for many generations. Even in species with relatively stable environments, there are theoretical reasons for expecting that a mixture of mobility and immobility would be adaptive (W. D. Hamilton, Narrow Roads of Gene Land, vol. 1, chapter 11). But it remains possible that 'Wrightian' processes are important in some cases. A particularly interesting case is the modern human species itself. After the dispersal of modern humans out of Africa, it is likely that human populations for most of the last 100,000 years were small and scattered, with little migration between different continental groups. These are good conditions for Wrightian genetic drift. Whether the observed differences in gene frequencies between continental populations are due to drift or selection remains an active area of research [see Jobling et al., passim]. Note 1. Neither Wright nor Fisher were very interested in genetic drift among genetic variants that are selectively entirely neutral, as expounded in Kimura's theory of neutral evolution at the molecular level. Fisher died before Kimura published his theory. Wright lived long enough to take account of it, and found it plausible enough with regard to neutral mutations of nucleotides, but considered it of no evolutionary interest (see Provine p.469-77). Note 2. As I understand it, Wright's conception of the distribution of gene frequencies is broadly is follows. We assume that two populations have evolved separately, and are fixed for different alleles at one or more loci. (For simplicity it is assumed that there are no more than two alleles at each locus.) The two populations are then combined and interbreed freely. Assuming that the populations are of equal size, the frequencies of the alleles at each locus in the combined population will initially all be 50%. The combined population then evolves in isolation. As a result of random genetic drift, the allele frequencies will tend to drift away from 50%. Over a large number of loci (or over a large number of hypothetical populations) we can ask, what is the probability that an allele will have any particular frequency after any specified number of generations? The total of such probabilities over all possible allele frequencies, from 0 to 1, will of course add up to 1, and will have an approximately smooth (continuous) distribution, which (on the given assumptions) will be symmetrical around a frequency of 50%. Initially the probability distribution will be clumped closely around 50%, but as time goes on it will spread out. Eventually, some alleles will begin to be lost or fixed, with a probability of 1/2N per generation. Wright now assumes that beyond a certain number of generations the shape of the probability distribution of frequencies for the remaining alleles will be approximately constant, apart from the continuing occasional loss and fixation of alleles, which will affect all the remaining alleles equally. The problem is to find this constant distribution under various assumptions about mutation, migration, and selection. Much of Wright's work in the 1930s was devoted to this problem. I cannot claim to have followed Wright's derivations in detail, as his explanations are obscure even by his usual standards. The problem is not just that the mathematics is advanced (though it does involve more calculus than in most of Wright's work) but that he makes various simplifying assumptions and approximations which are not self-evidently justified. I can only take it on trust that the conclusions are correct, and that if they were not (as Dobzhansky put it) 'some mathematician would have found it out'. References: [Provine] William B. Provine: Sewall Wright and Evolutionary Biology, 1986. [ESP] Sewall Wright: Evolution: Selected Papers, edited and with Introductory Materials by William B. Provine, 1986. D. S. Falconer: Introduction to Quantitative Genetics, 3rd edn., 1989. M. Jobling, M. Hurles, and C. Tyler-Smith: Human Evolutionary Genetics, 2004. John Maynard Smith: Evolutionary Genetics, 1989. Labels: Burbridge, Population genetics
Thursday, June 12, 2008
At other weblog a review of Jacob's Legacy: A Genetic View of Jewish History. Nothing new for readers of this weblog, but a respectable introduction to various topics which might surprise and interest many people.
Labels: Population genetics
Friday, June 06, 2008
Continuing my series of notes on the work of Sewall Wright, I come to the question of population size. This is important in Wright's formulation of population genetics and his evolutionary theory generally. One of the major differences between Wright and R. A. Fisher is that Fisher believed that, in general, evolutionary processes could be treated as if they took place in a very large random-mating population. He did not believe, contrary to some caricatures, that species were literally random-mating across their entire range (which is obviously false), but rather that there was usually enough migration between different parts of that range that for most purposes the departures from random mating did not matter. Wright, on the other hand, believed that in many cases local populations were sufficiently isolated from each other that they could be treated as populations evolving separately. This difference of views had a major impact on Wright's and Fisher's assessment of the relative importance of selection and genetic drift.
In his treatment of genetic drift Wright showed that in the absence of mutation and migration, genetic diversity, as measured by the proportion of heterozygotes in the population, will decline at a rate of 1/2N per generation, where N is the relevant population size. The larger the size, the slower the loss of diversity. This raises the question what is the 'relevant' size of N. As Wright explained in his great 1931 paper 'Evolution in Mendelian Populations', 'The conception is that of two random samples of gametes, N sperms and N eggs, drawn from the total gametes produced by the generation in question (N/2 males and N/2 females each with a double representation from each series of allelomorphs). Obviously N applies only to the breeding population and not to the total number of individuals of all ages' (p.111, 'Evolution: Selected Papers' (ESP). Unless otherwise stated, all citations are from this source.) Wright immediately goes on to say that this idealised model of the population is often an oversimplification. The effective size of the population is often different from the current actual number of breeding adults. If the effective size is smaller than the apparent size (the current number of breeding adults), genetic drift will be faster than expected. We may say that the effective size of the population is the size of an idealised population, meeting the criteria outlined in the quotation from p.111 given above, which would give rise to genetic drift at the same rate as actually observed. I am not sure that Wright ever formally defines effective size, but the definition I have suggested seems to be implied in various references, e.g. ESP pp.111, 157, 251, 354. Wright repeatedly specifies three factors which tend to reduce the effective size of the population below its apparent size: 1) different numbers of breeding males and females (ESP, pp.112, 251, 299, 354, 370). The effective population size is closer to that of the rarer sex. 2) where variance in reproductive success greater than that assumed in the idealised model (ESP pp. 112, 251, 300, 354, 270), genetic drift will be faster. 3) Occasional or cyclical reductions in population size (ESP pp.112, 157, 251, 300, 354, 370). The effect of (non-selective) reductions in population size is to take a random sample out of the gene pool. Such samples will have a variance in gene frequencies proportional to 1/n, where n is the size of the sample. The smaller the number n, the larger the variance due to 'sampling error'. If n is small relative to N (the usual population size), the effect is equivalent to concentrating many generations of slow genetic drift into a single event. In the absence of mutation and selection the effect is irreversible. A subsequent expansion of population, however large, does not reverse the loss of genetic diversity. (But note that if there is mutation and selection, an expansion of population gives an opportunity for rare advantageous mutations to appear and be selected. An expansion of population is also often associated with a relaxation of natural selection, which means that slightly disadvantageous mutations, which would normally be weeded out, may survive. This could help shift the population across a 'valley' in the adaptive landscape, if such things exist). These three factors all tend to reduce the effective population size below the current observed number of adult males and females. Wright repeatedly claims that the effective size is usually less than the apparent size, for example, 'The effective size (N) of the theory may, however, differ much from the apparent size, being usually much less' (ESP p.251). So far as I know, Wright only once mentions a factor that might increase the effective number above the apparent level: on ESP p.300 he mentions that the variance in reproductive success could be less than in the idealised model, in which case the effective population number could be up to twice the apparent size. But he comments that this improbable except in planned breeding experiments. So far so good. But so far as I am aware, Wright never mentions another factor which may raise the effective population size above the current number of breeding adults. This is where there is a large reserve of juvenile or dormant individuals with the ability to replace the current adults in the event of a population reduction. Such a reserve population would contain a greater amount of genetic diversity than the reduced number of current adults. This is probably a minor factor in the case of vertebrate animals, but could be important among some small invertebrates, where the number of eggs or larvae may be many times the current 'crop' of adults. It is even more important in the case of plants. Most species of plants produce resistant seeds, bulbs, etc, which are orders of magnitude more numerous than the mature plants. In some cases they can survive for years or decades in a dormant state. The genetic effect of sharp reductions in adult population numbers (e.g. due to drought) may therefore be much less among plants than among animals. This oversight vitiated one of Wright's own major empirical studies (see Provine p.485). Another major complication is migration. Wright's idealised model of genetic drift assumes that the population is completely self-contained, that is, reproductively isolated from other populations. If the population is an entire biological species, this is true by definition, since a biological species is defined by reproductive isolation. But if the population is a subdivision of a species, there is in principle the possibility that genes will enter the population from outside. My next note will examine how Wright dealt with this complication. William B. Provine: Sewall Wright and Evolutionary Biology, 1986. Sewall Wright: Evolution: Selected Papers, edited and with Introductory Materials by William B. Provine, 1986. Labels: Burbridge, Population genetics
Thursday, June 05, 2008
Gene Flow and Natural Selection in Oceanic Human Populations, Inferred from Genome-wide SNP Typing (H/T Dienekes):
It is suggested that the major prehistoric human colonizations of Oceania occurred twice, namely, about 50,000 and 4,000 years ago. The first settlers are considered as ancestors of indigenous people in New Guinea and Australia. The second settlers are Austronesian-speaking people who dispersed by voyaging in the Pacific Ocean. In this study, we performed genome-wide SNP typing on an indigenous Melanesian (Papuan) population, Gidra, and a Polynesian population, Tongans, by using the Affymetrix 500K assay. The SNP data were analyzed together with the data of the HapMap samples provided by Affymetrix. In agreement with previous studies, our phylogenetic analysis indicated that indigenous Melanesians are genetically closer to Asians than to Africans and European Americans. Population structure analyses revealed that the Tongan population is genetically originated from Asians at 70% and indigenous Melanesians at 30%, which thus supports the so-called "Slow train" model. We also applied the SNP data to genome-wide scans for positive selection by examining haplotypic variation, and identified many candidates of locally selected genes. Providing a clue to understand human adaptation to environments, our approach based on evolutionary genetics must contribute to revealing unknown gene functions as well as functional differences between alleles. Conversely, this approach can also shed some light onto the invisible phenotypic differences between populations. The stuff about candidates for selection: Our scans suggested no private mutation to exist on the Tongan autosomes that had reached fixation. However, there remain alternative possibilities that old-standing alleles have reached fixation by local selective pressures and that newly generated advantageous mutations have gained a high frequency but have not yet reached fixation. The block showing the lowest RM value (0.076) in the test of TGN vs EAS using method 1 was located at 92788024-92838919 on chromosome 12...which is at 41 kb distance from the CRADD gene...It is worth noting that an approximately 500 kb deletion around this gene in mouse has been reported to cause a high growth mutant that shows a proportional increase in tissue and organ size without obesity...Another candidate for the selected region in which an old-standing allele reached fixation was VLDLR...which is involved in triglyceride and fatty acid metabolism...In addition, overlapping signatures in both methods 1 and 2...were observed in the gene region of EXT2, which is a causal gene of the type II form of multiple exostoses and it plays a crucial role in bone formation...These genes can be candidates that are associated with the large fat, muscle, and bone masses of Polynesians. A recent paper examining the interpopulation differentiation of the type II diabetes-associated genes has suggested that a susceptible allele of PPARGC1A may play a role in the large difference in the prevalence of the disease between Polynesians and neighboring populations...However, our scans did not identify any signiture of positive selection on the gene region of PPARGC1A. Labels: Population genetics
Tuesday, June 03, 2008
In a previous post on current views on the human colonization of the world, I alluded two issues: whether modern humans displaced all archaics, and the precise demographic models under which that occurred. I placed more emphasis on the first, but was taken to task in the comments--apparently no one has issues with some version of the out-of-Africa story (ie. archaics contributed little genetic material to modern humans, if any), but there are some issues with the demographic models.
One paper pointed to is the Lohmueller et al. study on the high frequency of nonsynonymous polymorphisms in Europeans as compared to African-Americans. The authors do simulations under a variety of demographic scenarios, but rely heavily on a demography in which Europeans experienced a mild long-term bottleneck starting ~8000 generations (~160K years) ago, while the African populations instead experienced population growth. For those keeping track at home, humans aren't estimated to have left Africa until about 2000-4000 generations (40-80K years) ago. So these models rely on two populations having different demographies during a period of time before they split, an impressive feat indeed. So alright, some demographic histories aren't exactly the most believable. That said, all bottlenecks are not created equal. The fact remains that as you move away from Africa, each population contains a subset of the diversity of the ones the precede it--this is indicative of each population being founded by a subset of those preceding individuals. And allele frequency spectra, when measured in different populations (see the figure here), are inconsistent with constant population size in Europe and East Asia, and imply instead a bottlenck, stronger in E. Asia than in Europe, in recent demographic history. Any reasonable model has to take these observations into account. Labels: Population genetics
Thursday, May 29, 2008
John Hawks, in a post on scientists who dispute the acceleration hypothesis (acceleration deniers?), makes reference to "the Stanford school of genetic orthodoxy". So what is this?
Essentially, he's referring to the current paradigm (I'm as much of a fan of hyperbole as anyone else, but paradigm is clearly the more appropriate word here) in the field of population genetics about the peopling of the world. The story goes like this: a small set of individuals from an ancestral population in Africa moved somewhere in the Middle East, and grew. Then from there, a small set of individuals moved nearby in each direction and settled. Ditto for those populations, and so on. These "serial bottlenecks" kept occurring until the entire world was populated, replacing the individuals that were there before them. The observation that solidified this paradigm comes from this paper, which showed an impressive negative correlation between distance from East Africa and genetic diversity, consistent with each population containing a subset of the diversity of the populations it came from. Since then, that sort of approach has been used in a number of similar applications, including this nice one on the peopling of the Americas. Further support for this paradigm comes from more recent work modeling human demography--it's simply not true that this out-of-Africa hypothesis is enforced like an orthodoxy. See, for example this paper entitled "Statistical evaluation of alternative models of human evolution" (lest you think that alternative models of human evolution aren't being evaluated), which concludes for a single origin of humans in Africa. This doesn't test the "serial bottleneck" model, but does address the multiregional hypothesis, which I think is the major point for Hawks. Or consider a more recent paper, which attempts (with moderate success) to infer the colonization history of the world. The results favor out-of-Africa, as well as serial bottlenecks (though theses bottleneck, it must be noted, were essentially built into their model). Now, new data may alter some of these models somewhat--David Reich and other claim here (in a News and Views article) that they see evidence for multiple waves of migration from Africa in PCA analysis, though it remains to be seen how those results hold up. I'm not sure what Hawks thinks of these papers--for all I know, they're making the multiregional hypothesis into a statistical straw man that is easily demolished, but the point remains that the consolidation of these observations into a paradigm is not entirely without reason. The statistical methods and genetic data are available to challenge it, and skeptics (I know many) are more than welcome to try their hand. Labels: Population genetics
Positive selection on EDAR, why East Asians & Native Americans have thick hair
posted by
Razib @ 5/29/2008 01:36:00 AM
Positive Selection in East Asians for an EDAR Allele that Enhances NF-κB Activation:
Genome-wide scans for positive selection in humans provide a promising approach to establish links between genetic variants and adaptive phenotypes. From this approach, lists of hundreds of candidate genomic regions for positive selection have been assembled. These candidate regions are expected to contain variants that contribute to adaptive phenotypes, but few of these regions have been associated with phenotypic effects. Here we present evidence that a derived nonsynonymous substitution (370A) in EDAR, a gene involved in ectodermal development, was driven to high frequency in East Asia by positive selection prior to 10,000 years ago. With an in vitro transfection assay, we demonstrate that 370A enhances NF-κB activity. Our results suggest that 370A is a positively selected functional genetic variant that underlies an adaptive human phenotype. We've blogged about EDAR before; Could it be hair form?, EDAR controls hair thickness and EDAR and hair thickness. The story here is simple, before the populations ancestral to the Native Americans had left eastern Asia a mutation on the EDAR gene swept nearly to fixation among these populations. The derived SNP in particular is correlated with the thicker hair typical of East Asians and Native Americans. In other populations (Europeans, Africans, West and South Asians as well as Papuans and Melanesians) the SNP is in an ancestral state. The main twist in this study is that they used a molecular genetic technique to show that this derived state seems to upregulate the activity of NF-κB transcription factor. For the record, I'm really skeptical that this selective sweep occurred because the human populations of late Ice Age eastern Asia developed a really strong attraction to thick luxuriant hair with full body. The paper is Open Access, read the whole thing. Since the most interesting figure is either too small or too large, I've resized it appropriately and placed it below the fold.  Labels: Population genetics
Tuesday, May 20, 2008
Several of my previous notes have touched on the subject of Sewall Wright's F-statistics. The best known of these is FST, which is very widely used as a measure of the genetic divergence between sub-populations of a species. My aim in this note is to trace the evolution of the F-statistics in Wright's work.
Why F? A preliminary question is one of terminology. What, if anything, does the letter 'F' stand for? One plausible answer is that it stands for 'fixation', since among other things the F-statistics can be used to measure the rate at which alleles tend to be 'fixed'. Wright himself in his later writings sometimes refers to F as an 'index of fixation'. Plausible though this may be, it does not seem to be the origin of Wright's use of the letter F. This first appeared in his series of papers on 'Systems of Mating' in 1921, where he uses the letter F (in its lower-case form 'f') as a symbol for the 'correlation between uniting gametes' and as a measure of inbreeding. Although the word 'fixation' does occur in these papers, Wright does not say that 'f' stands for 'fixation'. The banal truth seems to be that by the time Wright needed a symbol to represent the correlation between uniting gametes, the letters a to e had already been allocated to other purposes, so that f was the first available letter in the alphabet. F as correlation between uniting gametes Wright's primary use of F (or f) is to designate the correlation between uniting gametes. The general idea of a correlation between gametes is now somewhat unfamiliar. If there are varying types of gametes in the population, uniting gametes may be said to be positively correlated if the same types tend to be paired together at mating, or negatively correlated if dissimilar types are paired. If the different alleles at a locus in the population are given notional numerical values, such as 0 and 1, a correlation coefficient for the correlation between pairs of uniting gametes can be calculated in the usual way. (For a fuller explanation see my post on Wright's measurement of kinship.) The resulting correlation coefficient is F. Heterozygosis and the correlation between gametes Also in 1921 Wright points out that the correlation between uniting gametes is connected with the proportion of heterozygotes in the population. Whether an individual is heterozygous at a locus is determined by the gametes (egg and sperm) of its parents which unite to form a zygote at fertilization. If they are identical at that locus, the offspring is homozygous, otherwise it is heterozygous. The proportion of heterozygotes (the level of heterozygosis) among the offspring, over and above the level expected with random mating, can be calculated from the correlation between uniting gametes, and vice versa. In SM1 Wright calculates that the percentage of heterozygosis is (1/2)(1 - f), where f is the correlation between uniting gametes. (This is stated without full proof, but I have checked it, calculating the correlation by the method of notional values.) This formula is only valid for the special case where there are two alleles with equal proportions of 1/2 in the population, but Wright soon (in 1922) generalised it to the case of two alleles with proportions of p and q = (1 - p), in which case the formula is 2pq(1 - f). He also began to use upper-case F, rather than f, as his preferred notation. F as a measure of inbreeding in a population A positive correlation between uniting gametes can arise in two ways (apart from mere sampling error): by assortative mating between similar phenotypes, or by mating between genetic relatives, in other words by inbreeding. Wright deals with both inbreeding and assortative mating, but gives more attention to inbreeding. If assortative mating is excluded, then F can be used as a measure of the average degree of inbreeding in a population. If the correlation between gametes is due solely to inbreeding, then the formula 2pq(1 - F) for the percentage of heterozygosis in a population can be given a simple interpretation in terms of Malecot's concept of Identity by Descent. The two genes at a locus in an individual are either Identical by Descent (IBD) from a common ancestor, or they are, by assumption, drawn randomly from the gene pool. In the first case they are certainly identical. In the second case, applying the familiar Hardy-Weinberg formula, they have a probability of (1 - 2pq) of being identical. Therefore if we interpret F as the probability that the two genes are IBD, on average for the population, the total probability that they are identical is F + (1 - F)(1 - 2pq) = 1 - 2pq(1 - F). Subtracting this from 1 to get the probability of heterozygosity we get the required formula 2pq(1 - F). F and the inbreeding of individuals The degree of inbreeding in a class of individuals (e.g. all offspring of matings between siblings) can be derived from an analysis of the way in which they are bred. The coefficient of inbreeding then measures the correlation between any pair of alleles at the same locus in an individual belonging to that class. The level of inbreeding in an offspring can be derived from the correlation between the uniting gametes of its parents, which in turn can be derived from the correlation between the parents themselves, in accordance with Wright's method of path analysis. The full method would involve considerations of dominance, heritability, and so on, but the coefficient of inbreeding is usually derived using a simplified method devised by Wright himself and expounded in several papers of the early 1920s (see especially paper 2 in ESP). In the simplest case, for the offspring of half-siblings who are not themselves inbred, Wright's formula gives a coefficient of inbreeding of 1/8. This is the same as the figure derived by the methods of Malecot for the probability in this case that the two genes at a locus in the offspring are identical by descent. In Malecot's approach this result is derived from explicit assumptions about probabilities. It is assumed that each gene in an offspring has a probability of 1/2 of coming from either parent, and - very importantly - that there is an independent probability of 1/2 that the same gene is inherited by any other offspring of the same parent. This is an assumption which is usually empirically correct (with certain exceptions such as sex chromosomes), but it is not logically necessary. For example, if surviving offspring came in pairs, each member of which received genes from complementary chromosomes in the parent, such pairs of offspring would have a lower correlation with each other than the usual calculations would suggest. It is therefore worth asking what features of Wright's approach take the place of the explicit probability assumptions in Malecot's system. The first key assumption, that each gene in an offspring has a probability of 1/2 of coming from either parent, is explicitly stated as a biological assumption (with the exception of sex-linked genes) in Wright's derivation of the path coefficient between offspring and parent. The other key assumption, that there is an independent probability of 1/2 that the same gene is inherited by any other offspring, does not seem to be explicitly stated. In SM1 Wright only directly calculates the correlation between parent and offspring. All other correlations, such as those between siblings, are derived indirectly from the parent-offspring correlation by the method of path analysis. The assumption of independent probabilities for each offspring seems to be built into the general assumptions of path analysis. In a late discussion of the principles of path analysis Wright emphasised that 'The validity of the system requires that any variable that enters into the system as a common factor back of two or more dependent variables, or as an intermediary in a chain, vary as a whole. If one part of a composite variable.... is more significant in one relation than in another, the treatment of the variable as if it were a unit may lead to grossly erroneous results' (EGP vol. 1 p.300). Fortunately, the assumption appears to be consistent with the usual pattern of genetic inheritance. Apart from special cases such as sex-linked genes, or MZ twins, it seems that each surviving offspring has an equal and independent probability of receiving any given allele from the same parent. This is despite the fact that during the formation of gametes the precursor-cells of the gametes are formed in pairs with complementary alleles from different chromosomes in the parent. In the case of eggs, only one of the proto-eggs formed from the same parental cell usually survives. In the case of sperms, so many sperms are produced in total that the chance of two sperms derived from the same parental cell both ending up in surviving offspring is negligible. F as a measure of inbreeding relative to a foundation stock One of Wright's original motives in devising his F statistics was to measure the effect of continued inbreeding over a number of generations. In agricultural (and laboratory) practice it is common for animals to be bred systematically over long periods using close relatives, e.g. mating sisters with brothers, or daughters with their fathers. With such practices the level of inbreeding among the offspring rises over the generations, and the level of heterozygosis declines. Wright's F-statistics provide a convenient method of measuring this process, superior to the previous ad hoc methods. The result of a number of generations of inbreeding within an inbred line can be summarised in the average F within that line, relative to the foundation stock (the population from which the inbred line is derived). The cumulative decline of heterozygosis since the inception of the line can then be calculated using the formula 2pq(1 - F). But this should raise questions about the precise meaning of F in such a case. F is in principle always a correlation coefficient, and could if necessary be expressed in terms of the Pearson product-moment formula. This requires the mean and standard deviation of the relevant statistical population to be specified. But what is the mean in the present case? The correlation is said to be 'relative to the foundation stock', so this appears to be the relevant statistical population, but the foundation stock no longer exists, and the correlated pairs are not part of it. So what is going on? Is F a legitimate correlation coefficient at all when more than one generation is involved? This puzzled me until I paid proper attention to page 169 of SM5. This gives the key to the mystery. Rather than just considering the correlation within a single inbred line, we must consider an indefinitely large (actual or hypothetical) ensemble of lines, all separately inbred according to the same system (e.g. sibling mating) for the same number of generations, and all derived from the same 'foundation stock'. The mean gene frequencies for the entire ensemble (or a large random sample thereof) should then be the same as in the foundation stock (in the absence of selection and mutation), but will vary within each particular inbred line according to the chance variations resulting from the reproductive process. F will therefore measure the average correlation within each such line as compared with the values of the foundation stock. Such a correlation coefficient will usually be hypothetical, since no such ensemble actually exists, but in principle it has a clear meaning consistent with the general method of correlation. The story so far The uses of F (or f) identified so far were all first described in Wright's ground-breaking 'Systems of Mating' in 1921. The different uses therefore cannot be put in a chronological sequence. Logically, however, the sequence is as follows: a) F as the correlation between uniting gametes. This is always the fundamental conception. b) F as a measure of average inbreeding in a population. In this sense it is closely connected to the level of heterozygosis. c) F as a measure of inbreeding in an individual. In this sense it is closely connected to the measurement of relatedness. d) F as a measure of continued inbreeding in a line relative to a foundation stock - see the last paragraph. F in natural populations As developed by Wright in 1921, the concept of F was heavily influenced by the circumstances of agricultural stock breeding, where mating is carried out in accordance with some deliberate plan. (Wright was employed in agricultural research for the US Department of Agriculture at the time - see Provine, chapter 4). The next major step was Wright's application of F to the measurement of genetic drift in natural random-mating populations. It is clear from Provine's biography that Wright first took this step around 1925, but the results were not fully published until the major paper on 'Evolution in Mendelian Populations' in 1931. I have discussed genetic drift in a previous post, and will not repeat that discussion here. The essential point is that in any finite population, over the course of time, there will be a tendency, purely by chance, for some lines of ancestry to be relatively successful, while others dwindle and eventually die out. The result is that, in the absence of selection or mutation, fewer alleles will account for a larger proportion of genes in the population, and the level of heterozygosis will decline. As a result of genetic drift, F tends to increase at a rate of approximately 1/2N per generation, where N is the size (strictly, the 'effective' size) of the random mating population. But F is still in principle the correlation between uniting gametes. Since the correlation between uniting gametes within a random mating population is zero, how can there be an increasing value of F? The answer is again that F is a correlation relative to the baseline of a 'foundation stock'. Wright does not, so far as I know, explain what exactly this means in the case of a natural random mating population, but I think we can understand it by analogy with the case of inbred agricultural breeding lines. We are to imagine that from a specified generation onwards a population is allowed to evolve by random genetic drift in a large number of hypothetical different ways. Within each of the resulting hypothetical descendent populations there will be a correlation between uniting gametes relative to the entire ensemble of hypothetical outcomes. The average of these correlations is constantly increasing. It is conceivable that in some cases the actual observed value of F - the correlation between uniting gametes within an actual population relative to that in the foundation stock - would be negative, but the expected average F is always positive. F in subdivided populations If a number of subgroups of a population breed within themselves in full or partial isolation from each other, the gene frequencies within them will tend to diverge from each other as a result of selection or genetic drift. Within each such subgroup, individuals will tend to be more similar to each other than to individuals randomly selected from other subgroups or from the entire population. Within the groups, individuals will therefore be positively correlated with each other relative to the entire population. Wright developed a system of F-statistics to analyse the structure of subdivided populations. This is one of his major contributions to population genetics after the fundamental paper EMP of 1931. The best-known of the F-statistics is FST, where S and T should ideally be subscripts, and stand for 'subpopulation' and 'total population'. The expression FST is possibly first used in a paper of 1950 (ESP p.585), but the underlying concept was first developed in a paper of 1943 on 'Isolation by Distance'. (I will cite this from the reprint in ESP, but it may be available online here. I downloaded it successfully once, but on another occasion got an error message.) Wright considers a population subdivided into a number of subpopulations of equal size, within which mating is random, and with two alleles at a locus. He shows, by a relatively simple but ingenious proof (ESP p.403), that in this case the correlation between uniting gametes within each subpopulation, relative to the total, is equivalent to Vp/pq, where Vp is the variance of the gene frequencies of the subpopulations (i.e. the mean square of their deviations from the frequency in the total population), and p and q are the frequencies in the total population. In 1943 this correlation is simply called F, but it is in fact the measure later known as FST. Wright recommends that the square root of F could usefully be taken as a measure of the genetic divergence between populations. (Of course, the rank order will be the same whether we take F itself or its square root as the measure.) It may also be noted that Vp/pq cannot be negative, as both the numerator and denominator are necessarily positive or at least zero. In general, a correlation coefficient may be either positive or negative, but in this case F measures the correlation due to the average differences between the gene frequencies of subpopulations, regardless of sign, and these cannot be less than zero. In the same 1943 paper, and in subsequent papers of the 1940s, Wright developed methods for dealing with correlations within hierarchically subdivided populations, where mating within each division may or may not be random. His terminology varied somewhat, but by 1950 he seems to have settled on the following (with IT, IS, and ST as subscripts): FIT: inbreeding coefficient of individuals relative to the total population FIS: inbreeding coefficient of individuals relative to the subpopulation FST: correlation between random gametes drawn from the subpopulation relative to the total population. (If mating is in fact not random within the subpopulation, this is a hypothetical correlation.) Wright shows that these measures are related by the equation FST = (FIT - FIS)/(1 - FIS). (For a relatively simple proof see EGP vol. 2 p.294-5, but note that the left square bracket in Equation 12.14 on that page is in the wrong place: it should be immediately before the first occurrence of qT.) It may be seen that if FIS is zero, in other words if mating within subpopulations is random, then FST = FIT. This is as it should be, since in this case the only source of correlation between individuals is the division of the population into subpopulations. FST then accounts for the entirety of the correlation within the total population, which is FIT. Wright's F-statistics are still widely used or alluded to, but are seldom understood in their original sense as correlation coefficients. Inbreeding within individuals is now usually explained by means of Malecot's Identity by Descent, while FST is usually explained in a way more appropriate to Masatoshi Nei's GST. Wright's work was however clearly the inspiration and foundation for the work of these later geneticists. A few cautions about the use of FST may be useful. a) Wright originally intended FST to be calculated as an average over a large number of subpopulations. In theory, it would be possible to calculate it for as few as two subpopulations, in which case, if they are of equal size, FST is d^2/pq, where d is the deviation of the subpopulation frequencies from the frequency in the total population. So far as I know, Wright himself never used it in this way. b) FST is calculated from gene frequencies on a locus-by-locus basis. It may well vary from one locus to another. To get an indication of the extent of evolutionary divergence between subpopulations, it is desirable to take the average FST over a large number of loci. c) FST is not simply proportional to the length of time or number of generations that two subpopulations have been diverging. Other factors such as the amount of migration between them and the size of the populations are also relevant. Small populations diverge by genetic drift far more quickly than large ones. d) Wright intended FST mainly to be used for genes that are not subject to significant natural selection. Genes that are under selection may diverge either more or less in different subpopulations than an average FST would suggest. References: William B. Provine: Sewall Wright and Evolutionary Biology, 1986. Sewall Wright: Evolution: Selected Papers, edited and with Introductory Materials by William B. Provine, 1986. (ESP) Sewall Wright: Evolution and the genetics of populations, 4 vols., 1968-1978. (EGP) Labels: Burbridge, Population genetics
Thursday, May 08, 2008
Continuing my series of notes on the work of Sewall Wright, this one deals with the subject of genetic drift. I had originally planned to call this note 'Inbreeding and the decline of genetic variance', but anyone interested in the matters covered here, and searching for them on the internet, is far more likely to search for 'genetic drift'. This is one of the subjects most closely associated with Wright, to the extent that genetic drift was formerly often known as the 'Sewall Wright Effect'. My main aim is to help people follow Wright's own derivation of his key results, and to clarify the relationship between genetic drift and inbreeding.
I will refer mainly to the papers reprinted in the collection Evolution: Selected Papers, (ESP) and especially the monumental 1931 paper on 'Evolution in Mendelian Populations', which is available online here. Anyone interested in Wright should also read William B. Provine's biography of him. If in these notes I occasionally make critical remarks on Provine, it should not detract from the general excellence of his book. See the References for details. In an infinitely large population, in the absence of selection and mutation, the proportions of different gene types (alleles) in the population will remain unchanged indefinitely. But real populations are never infinitely large, and gene frequencies will fluctuate to some extent by chance. As Wright put it in 1931, 'Merely by chance one or the other of the allelomorphs [alleles] may be expected to increase its frequency in a given generation and in time the proportions may drift a long way from the initial values' (ESP, p.107.) The general nature of drift can be illustrated by the hackneyed example of coin tossing. If we simultaneously toss a number of 'fair' coins, and repeat the trial a large number of times, then the average proportion of heads, by the definition of a fair coin, will be 1/2, and the average number of heads per trial will be N/2, where N is the number of coins in a trial. More generally, suppose the probability of heads for each coin is always p, where p is any fraction between 0 and 1. The long term average number of heads per trial will then be Np. But on any particular trial, purely by chance, the number of heads is likely to deviate from the average. It can be shown that the variance of the number of heads per trial is Npq, where q = 1 - p. [Note 1] If we are interested in the proportion of heads per trial (the number of heads divided by N), it can be shown that the variance of the proportion is pq/N. [Note 2] On each trial, the proportion of coins is therefore likely to deviate from the long term average by a quantity related to pq/N. Departing now from the real behaviour of coins, let us suppose that the value of p on each trial is determined by the proportion of heads in the previous trial. The proportion of heads will then drift up and down in a 'random walk' pattern, with the size of the 'steps' being inversely related to the size of N. If N is very large, each step will be small, but if N is small the steps may be relatively large. If, by chance, the proportion of heads in a trial ever reaches 1 or 0, then p for all future trials will also be 0 or 1, and heads (or tails) will be permanently 'fixed'. This is very likely to happen sooner or later. Genes are not coins, so the analogy is not perfect. In a population of genes, the replication of each gene is not a simple matter of 'heads or tails', as each gene may have 0, 1, 2 or more descendants. Also, while the number of coins is assumed to be fixed at N, a biological population is seldom absolutely fixed in size. Nevertheless, there are important similarities. In the absence of selection, it is a matter of chance whether or not a particular gene enters an egg or sperm and then survives to reproduce again in the next generation. Suppose that there are two alleles, A and B, at each locus, with the frequencies p and q in the population. In the absence of selection and mutation, these will also be the expected frequencies in the next generation. In a population of N diploid individuals, there are 2N genes in the population at each locus. In a stable population there will still be 2N genes in the next generation. We can schematically represent reproduction as a 'trial' consisting of 2N events, each involving the random choice of a gene to enter the new generation, with probabilities of p and q for the 'outcomes' A and B at each choice. The probabilities of obtaining the various possible combinations of A's and B's are then given by the expansion of the binomial (p + q)^2N. Wright himself uses this model of the process on several occasions, e.g. ESP p.289. While this may seem a very artificial way of viewing reproduction, it is not as unrealistic as it seems. Suppose that N diploid individuals each have the same number of offspring, the number being large, and certainly large enough to ensure that there are at least 2N copies of each allele among the population of offspring. Then select N of the offspring as 'survivors', completely at random, which is analogous to survival in a resource-limited population without natural selection. The probability of the various possible gene frequencies will then be approximately as in the schematic model (with the complication that in a finite population of offspring the probability of selecting an offspring with a given allele will be affected by the number already selected, e.g. if nearly all the alleles of a given type have, by chance, already been selected, the probability of selecting another one will be much reduced). Nothing has so far been said about inbreeding. Moreover, the processes just described would apply not only to sexually reproducing organisms but also to asexually reproducing organisms and genetic elements, such as mitochondria and Y chromosomes, where the possibility of inbreeding does not arise. But in Wright's treatment of the subject, references to inbreeding are frequent, and the rate of genetic drift is derived by an argument which seems to depend on the existence of inbreeding. For example, on p.165 of ESP he says: 'If the population is not indefinitely large, another factor must be taken into account: the effects of accidents of sampling among those that survive and become parents in each generation and among the germ cells of these, in other words, the effects of inbreeding'. Such statements are likely to give the impression that inbreeding is fundamental to the process of genetic drift. How can this be? The explanation is that in a sexually reproducing population a convenient measure of genetic drift is the changing proportion of homozygotes, and the existence of homozygotes is related to inbreeding. If a given allele has ultimately arisen from a single mutation, then homozygous copies of that allele can only occur in the same individual if that individual is descended from the same ancestor by at least two paths, which is by definition inbreeding. Even if the allele has more than one origin, the level of inbreeding in the population will affect the level of homozygosis. But as the example of asexual organisms shows, there is no necessary connection between genetic drift and inbreeding. R. A. Fisher, in his different approach to the subject, does not (I think) ever refer to inbreeding. Confusing the two things would be like confusing the study of heat with the study of thermometers. It may therefore be wondered why Sewall Wright took his particular approach. The answer may be partly that his mathematical training was less advanced than Fisher's, so that he was obliged to use less mathematically sophisticated methods. This has the advantage that his work on the subject is in principle accessible to a wider range of readers. Moreover, on one important point Wright's methods got the correct result where Fisher, through neglecting a quantity which turned out not to be negligible, got the wrong result by a factor of 2 (as Wright never tired of pointing out). But I think the main reason for Wright's approach was that he first investigated genetic drift in the context of agricultural breeding, where livestock are often closely inbred. In this context one of the main concerns is to quantify the loss of genetic variation in each particular inbred strain. It was therefore natural for Wright to approach the subject by measuring the loss of heterozygosis associated with inbreeding. When he later turned to consider genetic drift in natural populations, where mating is approximately random, he continued to use the methods he had already devised for the study of inbreeding in agriculture. (I will not now explore the precise meaning of Wright's coefficients of inbreeding (the famous F-statistics) which I hope to deal with in another note.) Wright's most important finding was that heterozygosis (the proportion of heterozygotes in the population) tends to decline at a rate of 1/2N per generation, where N is the diploid population size. (This assumes that males and females each have a population size of N/2.) Most textbooks give a simplified version of Wright's derivation of this result. Wright's own treatment, in EMP, is difficult to follow, and in view of its importance I have provided a guide in Note 3 below. Even the simplified textbook versions are not always very clear, and I do not know of any wholly satisfactory account. Key assumptions are often not clearly stated or justified. Two relatively good accounts are those of Falconer and Maynard Smith (see Refs.) I will outline a derivation based mainly on Falconer (with some modifications). Let us assume there is a population of N diploid individuals. Generations are separate. There is no mutation or natural selection in the period under consideration. The n'th generation is designated Gn, the previous generation by Gn-1, the following generation by Gn+1, and so on. The probability that the two genes at the same locus in an individual of Gn are identical is designated CIn, where CI stands for 'coefficient of inbreeding'. (For my approach here it is not necessary to specify whether the genes are identical 'by descent'.) The probability that two randomly selected genes at the same locus in two different individuals of Gn are identical is designated CKn, where CK stands for 'coefficient of kinship'. For the simplest case, consider a population of hermaphrodites which are capable of self-fertilisation and mate completely at random, including with themselves. (This would be approximately true of some marine invertebrates which release gametes into the water.) From the assumptions of random mating and non-selection it follows that any individual in Gn is equally likely, with probability 2/N, to be a parent of any individual in Gn+1 (since in a stable population each individual will have on average have 2 out of the N surviving offspring). It does not follow that, if we select at random an individual in Gn+1, and then select another, there is a probability of 2/N that the second individual will have the same father (or mother) as the first. For example, if each individual in Gn produced exactly 2 surviving offspring, the probability that a second randomly selected individual in Gn+1 had the same father (or mother) as the first would only be 1/(N-1). To get a probability of 2/N we require an additional assumption, which is technically satisfied by specifying that the number of offspring for individuals follows a Poisson distribution. (This assumption is mentioned by Maynard Smith but not by Falconer.) With these assumptions, it follows that CIn equals CKn. In the case of CIn, we select a gene at random in Gn, and then inquire whether the other gene at the same locus in that individual is identical. In the case of CKn, we select a gene at random in Gn, and then inquire whether another randomly selected gene at the same locus in a different randomly selected individual is identical to the first gene. But in both cases each gene is a copy of a gene taken absolutely at random from all the genes in Gn-1. The probabilities of identity are therefore the same, and CIn therefore equals CKn. By the same argument it follows that any two randomly selected distinct genes at a locus in Gn have the same probability of being identical, whether they are in the same or different individuals. If we call this probability CDn, we have CDn = CIn = CKn, for any value of n. But CIn can be broken down into two component probabilities. With probability 1/2N, the two genes at a locus in the same individual are copies of the very same gene in Gn-1, in which case they are certainly identical. In all other cases, therefore with probability 1-1/2N, they are copies of two distinct genes in Gn-1, in which case there is a probability CDn-1 that they are identical. But CDn-1 = CIn-1 (since the equality CDn = CIn applies for any value of n). The total probability CIn therefore comes to CIn = 1/2N + (1 - 1/2N)CIn-1. The coefficient of inbreeding in one generation is therefore derivable from the coefficient in the previous generation by a formula involving the addition of 1/2N. It can further be shown, with a little algebraic manipulation, that heterozygosis tends to decline by a factor of (1 - 1/2N) per generation (see Falconer p.64-5 for a proof). If self-fertilisation is excluded, two genes in the same individual cannot be copies of the very same gene in the previous generation, so the analysis needs to be pushed further back. If mating between different individuals is completely random, including siblings, then CIn = CKn-1. If mating between siblings is excluded, but otherwise random, CIn = CKn-2, and so on. But it is always possible to express the 'coefficient of inbreeding' in one generation in terms of the coefficients in previous generations, and heterozygosis always tends to decline by a factor of (1 - 1/2N) per generation (assuming equal numbers of males and females). The above argument, like Wright's own, measures the progress of genetic drift by the decline of heterozygosis and the associated increase in the coefficient of inbreeding. It should however be clear that this is not essential. If we wanted to study genetic drift in asexual haploid replicators, such as Y chromosomes, it would be possible to modify the derivation to use only coefficients of kinship, rather than inbreeding. More fundamentally, the process of genetic drift depends not on inbreeding but on the existence of variance in reproductive success. Some genes have no descendants, some have only one, and some have more than one. Over the course of time, more and more lines of descent die out, and the surviving genes are collectively descended from fewer and fewer original ancestors. Ina sexually reproducing population this also leads to increased levels of inbreeding, in a broad sense. If there were no such variance in reproductive success - if every gene had exactly the same number of surviving 'offspring' - there would be no genetic drift. Among diploids, the variance in replication of individual genes is due to two factors: the variance in the number of surviving offspring, and the random allocation of genes to gametes in the process of meiosis. Even if every diploid individual had exactly the same number of surviving offspring, there would still be variance in the replication of individual genes for the second reason. As for the variance in the number of offspring, the assumption of a Poisson distribution is probably not unreasonable in many species, but there could be departures from it in both directions (i.e. either greater or smaller variance). There might also be different variance in the two sexes. For example, among animals like Elephant Seals, the variance among females might be rather small, because all females have a low but steady rate of reproduction, whereas among males the variance would be much higher, as many males have no offspring at all, while a few have a large number. Wright takes account of some of these factors in his discussions of 'effective population size', This note has only dealt with a few aspects of Wright's work on genetic drift. I have tried to identify the underlying assumptions and (in Note 3) to clarify Wright's most important derivation. None of this says anything one way or the other about the actual importance of genetic drift in evolution. What should be clear is that genetic drift is a weak force except in very small populations, since its effect is inversely proportional to population size. In large populations it would be overpowered by modest rates of selection or migration. (The other factor to consider is mutation, but except in large populations this is an even weaker force than drift, as mutation rates are typically of the order of only 1/100,000 per generation.) I hope to deal with some of these issues in further notes. Note 1: Suppose we toss a single coin K times, where K is a large number. If the probability of heads is p, the total number of heads will be Kp and the average number of heads per toss will be Kp/K = p. But on each particular trial (the toss of a single coin) there can only be 1 or 0 heads, so we will have Kp trials with the deviation value (1 - p), and K(1 - p) trials with the deviation value (0 - p) = - p. Using the abbreviation q for (1 - p), the variance of the number of heads for trials consisting of a single coin toss is therefore [Kpq^2 + Kqp^2]/K = pq^2 + qp^2 = pq(q + p) = pq. It may seem odd to speak of the variance of the number of heads in trials where there is only one coin per trial, but in principle it is legitimate, and it enables us easily to derive the variance of the number of heads where the trials involve N coins. Since the variance of the sum of a number of independent numerical values equals the sum of the variances of the values individually, the variance of the number of heads in N independent coin tosses, each with variance pq, is simply Npq. Note 2: The average proportion of heads per trial of N coin tosses, each with probability p, is in the long term p. If X is the number of heads in any particular trial of N coins (where X is a variable), the deviation values of the proportions will be of the form X/N - p = (X - Np)/N, and the variance of the proportions in K trials will be S[(X - Np)/N]^2]/K. But S[(X - Np)/]^2]/K is the variance of the number of heads, which has been proved equal to Npq, so the variance of the proportion is Npq/N^2 = pq/N. Note 3: This is a commentary on pages 108-110 of ESP, which reprints pages 107-109 of the original paper EMP (the near identity of pagination is just a coincidence). I will mainly be concerned with page 109 of ESP, where Wright derives his fundamental results for the decline of heterozygosis. In following the derivation it is necessary to refer back frequently to the definitions at the bottom of page 108. Wright assumes that the sexes are separate (so there is no self-fertilisation) but that mating is otherwise completely random, including between siblings. He assumes that there are Nm breeding males and Nf breeding females. With random mating, he states that the proportion of matings between full siblings is 1/NmNf. This evidently assumes that there is a probability of 1/Nm that two mates have the same father, and an independent probability of 1/Nf that they have the same mother (note that m and f stand for male and female, not mother and father). This is actually a strong assumption, which ought to be clearly stated. It assumes (a) that the number of offspring of individuals follows a Poisson distribution (or something similar) and (b) that parents have male and female offspring in the same proportions as in the population generally. This is not necessarily true: for example if some parents had a strong bias towards producing male or female offspring, the probability of mating between siblings would be reduced. (Wright does discuss some of these considerations in the section on 'The Population Number' at pp.111-12 of ESP.) Wright then gives the proportion of matings between half siblings, and between all less closely related individuals. These depend on the same assumptions as for full siblings. He then gives a formula for M, the correlation between mates in the current generation. Note that the formula is of the form a'^2b'^2[Z], where Z is a complicated expression in square brackets. From the definitions on p.108 we have a'^2b'^2 = [1/2(1 + F')][(1 + F'')/2], so we have M = [1/2(1 + F')][(1 + F'')/2][Z]. The expression Z can be derived by Wright's method of path analysis. The first component of Z deals with the case of mating between full siblings. If we label the siblings A and B, and their parents C and D, we have two 'direct' paths, ACB and ADB, and two 'indirect' paths, ACDB and ADCB, which involve the correlation M' between mates in the previous generation. Hence the coefficient (2 + 2M') for the first component. For half siblings A and B, there is one shared parent C and two non-shared parents D and E, so there is one direct path, ACB, and the three indirect paths ADCB, ADEB, and ACEB, giving the coefficient (1 + 3M'). For unrelated mates A and B, with the non-shared parents C, D, E and G (to avoid using F, which is already in use), we have no direct paths and four indirect paths, ACGB, ACEB, ADEB, and ADGB, giving the coefficient 4M'. Next Wright derives an expression for F, the correlation between uniting gametes in the current generation. Here we must note from p.108 that F = b^2M, and b^2 = (1 + F')/2. Using the expression M = [1/2(1 + F')][(1 + F'')/2][Z], we therefore have F = [(1 + F')/2][1/2(1 + F')][(1 + F'')/2][Z] = [(1 + F'')/8][Z]. With a little manipulation, and using the full expression for Z, this can be put in the form F = (1 + F'')[Nm + Nf - M'Nm - M'Nf + 4F'NmNf]/8NmNf . But now we should note that M' is the correlation between mates in the previous generation. We can therefore adapt the equation F = b^2M to get the corresponding equation for the previous generation, i.e. F' = b'^2M'. But b'^2 = (1 + F'')/2, so F' = [(1 + F'')/2]M', and therefore M' = 2F'/(1 + F''). Substituting 2F'/(1 + F'') for M' in the equation F = (1 + F'')[Nm + Nf - M'Nm - M'Nf + 4F'NmNf]/8NmNf, it follows by some grinding but essentially routine algebra that F = Q, where Q is the expression on the right of the second equation on page 109. Then using the definition of P, P', etc, in terms of F, F', etc, the third equation also follows by routine algebra. This leaves the final death-defying leap to the fourth equation. This is not helped by the puzzling statement that we can equate P/P' to P/P''. This would imply that the proportional change per generation was not just constant but zero, and P/P'' must surely be a misprint for P'/P''. (The fact that this horrible error is not corrected or commented on in the ESP reprint leaves me wondering how closely Provine, as editor, has followed the details of Wright's text.) But even with this correction, it is far from obvious how Wright derives his fourth equation. I had given up hope of solving it until I was reading volume 2 of EGP, and found a discussion of the simpler case of random mating hermaphrodites, which fills in a few gaps in the derivation (see EGP vol 2, p.194-5). First, it confirms the suspicion that P/P'' should be P'/P''. Second it shows (or at least hints) how the problem can be reduced to a quadratic equation. Taking these hints, we can apply them to the fourth equation on p.109. First, rearrange and simplify the third equation to get P - P'[1 - (Nm + Nf)/4NmNf] - P''(Nm - Nf)/8NmNf = 0. Then divide through by P'' to get P/P'' - (P'/P'')[1 - (Nm + Nf)/4NmNf] - (Nm - Nf)/8NmNf = 0. But by assumption P/P' = P'/P'', so P/P'' = (P'/P'')^2 = (P/P')^2. We can therefore treat the equation as a quadratic of the form ax^2 + bx + c = 0, with x = P/P'. This can be solved by the standard method to get (as the larger of the two roots) P/P' = (1/2)[1 - (Nm + Nf)/4NmNf)] + (1/2)[root(1 + [(Nm + Nf)/4NmNf]^2)]. This is nearly Wright's fourth equation. For the final step, we take deltaP to mean P - P', so that - deltaP/P' = - (P/P' - 1). We therefore need only subtract 1 from the expression (1/2)[1 - (Nm + Nf)/4NmNf)] + (1/2)[root(1 + [(Nm + Nf)/4NmNf]^2)], and then reverse the sign, to get Wright's fourth equation. After this tortuous derivation, the discussion on page 110 of ESP is relatively plain sailing. The only slight puzzle is how Wright gets the approximation at the top of the page. I deduce that he uses the fact that when a is a small fraction, root(1 + a) is approximately equal to 1 + a/2. Taking [(Nm + Nf)/4NmNf]^2 as a, and grinding through the algebra, Wright's approximation can then be verified. Overall, as often with Wright's work, I am torn between admiration for his ingenuity and frustration at his obscurity. References: D. S. Falconer: Introduction to Quantitative Genetics, 3rd edn., 1989. (The 4th edn., by Falconer and Mackay (1995) appears to be the same so far as its treatment of genetic drift is concerned.) John Maynard Smith: Evolutionary Genetics, 1989. William B. Provine: Sewall Wright and Evolutionary Biology, 1986. Sewall Wright: Evolution: Selected Papers, edited and with Introductory Materials by William B. Provine, 1986. Sewall Wright: 'Evolution in Mendelian Populations', Genetics, 16, 1931, pp.97-159. (Reprinted at pp.98-160 of ESP.) Sewall Wright: Evolution and the genetics of populations, 4 vols., 1968-1978. Labels: Burbridge, Population genetics
Monday, April 21, 2008
 The caption: The first column shows the theoretical expected PC maps for a class of models in which genetic similarity decays with geographic distance (see text for details). The second column shows PC maps for population genetic data simulated with no range expansions, but constant homogeneous migration rate, in a two-dimensional habitat. The columns marked Asia, Europe and Africa are redrawn from the originals of ref. 3 [this reference is to Cavalli-Sforza's The History and Geography of Human Genes]. Each map is marked by which PC it represents. The order of maps in each of the last three columns was chosen to correspond with the shapes in the first two columns. What does this mean? The authors say it best in the abstract: Nearly 30 years ago, Cavalli-Sforza et al. pioneered the use of principal component analysis (PCA) in population genetics and used PCA to produce maps summarizing human genetic variation across continental regions. They interpreted gradient and wave patterns in these maps as signatures of specific migration events. These interpretations have been controversial, but influential, and the use of PCA has become widespread in analysis of population genetics data. However, the behavior of PCA for genetic data showing continuous spatial variation, such as might exist within human continental groups, has been less well characterized. Here, we find that gradients and waves observed in Cavalli-Sforza et al.'s maps resemble sinusoidal mathematical artifacts that arise generally when PCA is applied to spatial data, implying that the patterns do not necessarily reflect specific migration events. Labels: Population genetics
Friday, April 11, 2008
Most people with an interest in genetics will be aware that Sewall Wright made major contributions to the theory of kinship or relatedness. Fewer people will have any direct knowledge of his work on the subject, and those who do consult his writings may find them difficult. The present note is intended to help those who want to tackle Wright at first hand. See also this evaluation by the geneticist W. G. Hill.
Most of Wright's key ideas on the subject were first presented in a 5-part paper on 'Systems of Mating' (SM) in 1921. All 5 parts can be found on the internet with a little searching. SM1, which is the most fundamental, is here, and SM5, which contains a relatively un-technical summary, is here. Rather than go straight to Wright's own approach, I will begin by comparing and contrasting it with that of the French geneticist Gustave Malecot, based on the concept of Identity by Descent. Malecot first introduced his methods around 1940, and since then they have supplanted Wright's approach, to the extent that Wright's own methods have been almost forgotten. What is presented in textbooks as due to Wright is often in reality due to Malecot. The two approaches do have some similarities, and in simple cases they lead to the same quantitative results, but there are also some important differences. Malecot and Identity by Descent In Malecot's system two genes at the same locus, in the same or different individuals, are defined as Identical by Descent (IBD) if they are both descended from the very same individual ancestral gene, without either of them undergoing mutation in the interim. The relatedness between two individuals can be measured, roughly speaking, by calculating the probability that two genes at the same locus in the two individuals are IBD. To do this it is necessary first to identify all the distinct paths of descent connecting the two individuals through a common ancestor, and then to calculate the probability that the same gene will have descended to both individuals from that ancestor along any given path. Since all such paths of descent are mutually exclusive (though portions of them may overlap), the resulting probabilities can be added together to give the total probability that a given gene in the two individuals is IBD. To take a simple case, consider two individuals (full siblings) who have both parents in common. I assume that the parents are not related to each other or inbred. If we select a (diploid autosomal) gene at random from one sibling, there is a probability of one-half that it comes from the mother, and, if it does, a probability of one-half that the same gene has descended from the mother to the other sibling. This gives a compound probability of one-quarter that the second sibling has received a gene from the mother that is IBD to the selected gene in the first sibling. There is likewise a probability of one-quarter that the second sibling has received an IBD copy from the father. The total probability is therefore one-half, which is often called the Coefficient of Relationship or Relatedness between full siblings. If the parents are themselves related or inbred (i.e. descended from one of their own ancestors by more than one possible path), additional paths of descent need to be taken into account. Since there are two genes at the relevant locus in the second sibling, there is a probability of one-quarter (one-half times one-half) that a particular one of these genes, chosen at random, is IBD to the selected gene in the first sibling. This is usually known as their Coefficient of Kinship. If a male and female with a non-zero Coefficient of Kinship mate together, there is a non-zero probability that any offspring will inherit two genes that are IBD to each other. This is usually known as the offspring's Coefficient of Inbreeding, and a little consideration shows that it is equal to the Coefficient of Kinship of the parents. A point left vague in some accounts is how far back the paths of ancestry can or should be traced. There would be little point in tracing them back so far that the gene would probably have mutated along the way to one or both descendants, but with a mutation rate of only about 1 in 100,000 per generation this is not a major constraint. In practice, ancestry is seldom traced back beyond five or six generations, as the probability of Identity by Descent along any given path going beyond than this is very small (less than 1 in 1,000), and the aggregate probability along all such paths will usually be much the same for all individuals in the same population. Wright and the Correlation between Relatives None of this is directly due to Sewall Wright. He does uses path diagrams similar to those of Malecot (who was inspired by Wright's work), but the quantities measured along the paths are not probabilities of Identity by Descent but path coefficients. As discussed in my note on Wright's method of Path Analysis, the correlation between two variables can be derived from the path coefficients along the paths connecting them. The measures of relationship between two individuals in Wright's system are always in principle correlation coefficients. In simple cases (no inbreeding, no dominance, no assortative mating, and so on) they are quantitatively the same as Malecot's measures, but in principle they are quite different. Three important differences should be emphasised: a) like all correlation coefficients, Wright's measures of relationship are valid only relative to a specified statistical population. The coefficient of relationship between two individuals may well vary according to the specified population; e.g. it may be different if the specified population is an ethnic group to which the individuals belong as compared with a population comprising several ethnic groups. b) unlike probabilities, which are always positive, a correlation coefficient can be either positive or negative. In fact, although Wright seldom discusses negative relationships, within any specified population they are in principle as common as positive relationships. c) relative to any specified population, the correlation between two randomly selected individuals from that population is zero (apart from sampling error). This point has sometimes been overlooked, for example in discussions of Hamilton's Rule. The 'r' in Hamilton's Rule should be a regression coefficient rather than a correlation coefficient (as Hamilton realised around 1970 - see Narrow Roads of Gene Land, vol. 1, p.179), but the same principle applies: the regression of one randomly selected individual on another randomly selected individual, relative to the population from which they are randomly selected, is approximately zero. Hamilton's Rule therefore predicts that altruistic behaviour will not be directed randomly towards all members of the relevant population, though it may be difficult to decide which population is 'relevant' for the purpose. I emphasise these points partly because Wright himself does not. They are implicit in the use of correlation coefficients, but Wright seldom explicitly mentions them. An exception is in SM5, where Wright points out that the correlation between relatives within an inbred line will be small although relative to the wider population it is large. Some more general statements are made in Wright's late work on Evolution and the Genetics of Populations (EGP). In volume 2 of that work (1969) he says that 'In a panmictic [randomly mating] population, there is no correlation between homologous genes of uniting gametes relative to the gene frequencies in the whole population. On splitting up into small lines which breed within themselves, a correlation between uniting gametes is to be expected.... The relativity referred to above has sometimes been overlooked or misinterpreted. A correlation coefficient is, of course, always relative. It is a property of the population as well as the two variables....' (pp.175-77.) Wright goes on to discuss Malecot's method of Identity by Descent. He accepts that it is a useful technique and often leads to the same results as his own, but argues that his own approach is more general and in particular that his own concept of relationship allows for negative values. Wright is often vague about the population in which the correlations are to be measured, leaving this to be inferred from the context. Sometimes the relevant population is the entire generation to which the correlated individuals belong, sometimes it is a defined sub-population, but sometimes it seems to be a 'foundation stock' from which they are descended. This is problematic, as it seems to require a correlation between individuals relative to the means and standard deviations in a population to which they do not themselves belong. I will discuss this further in dealing with Wright's work on inbreeding and genetic diversity. Correlations between notional values Wright was not the first person to work on the correlation between relatives. Unknown to Wright, R. A. Fisher had already treated the subject at length, by different methods, in 1918. In fact, the subject goes back at least to 1904, when Karl Pearson considered the correlations to be expected on the hypothesis of Mendelian dominant inheritance. He found that (on certain simplified assumptions) the correlation between parent and offspring would be only one-third, rather than the correlation of about one-half usually found in empirical data on human traits. Pearson considered this a serious objection to the generality of the Mendelian theory. One of the aims of Fisher's 1918 paper was to show that, when complications such as assortative mating were taken into account, the data were consistent with widespread Mendelian dominance. The idea of a correlation between relatives is intelligible enough when the correlation involves continuous phenotypic traits such as height, but it is more obscure when the traits are purely qualitative, or when the correlation is not between phenotypes but between gametes or genotypes. If there are varying types of gametes or genotypes (e.g. different alleles at a locus) in the population, they may be said to be positively associated if the same types tend to occur together, more often than would be expected by chance, in the same individual or in certain pairs of individuals. There are several useful measures of the 'association' of qualitative variables (see any edition of G. U. Yule's Introduction to the Theory of Statistics). However, Wright (like his predecessors) preferred to use the Pearson product-moment correlation coefficient. To obtain a Pearson correlation coefficient in the case of purely qualitative variables, such as differences between alleles, it is necessary to give the correlated items notional algebraic or numerical values. Since these are to some extent arbitrary, it might be feared that this would introduce an arbitrary element into the results, but in the cases of interest the arbitrary values cancel out and leave the correlation coefficient itself unaffected. The procedure can be illustrated by the problem of dominance, which is treated by Wright in SM1, page 117-8. If we assign the homozygotes AA and aa the arbitrary values 1 and 0 respectively, in the case of complete dominance of A, the heterozygote Aa will have the value 1, while in the case of zero dominance it will have the value 1/2. Each individual in the population will therefore have a pair of numerical values, under the assumptions of dominance and non-dominance respectively. For homozygotes the two values will be the same but for heterozygotes they will be different. If the frequencies of the various genotypes in the population are specified, the means and standard deviations of the numerical values can be calculated, and the covariance and the correlation coefficient between the pairs of values can then be derived in the usual way. The correlation coefficient will be unaffected if one or both variables are systematically multiplied by or added to a constant (see Notes on Correlation, Part 2). But this entails that we would get the same correlation if we chose any other set of arbitrary values as alternatives to 0 and 1, provided the value of the heterozygote in the absence of dominance is half-way between that of the homozygotes. We can therefore obtain a quite general result for the correlation between the values of genotypes with and without dominance. (Of course, correlations could be calculated in a similar way on different assumptions about dominance, e.g. for partial dominance.) It can be shown by this method that Wright's results at the bottom of page 117 are correct, though I do not see how Wright derived his particular formulae, which are far from obvious. [As I have mentioned elsewhere, the equation p = root-uv appears to be a printing error or slip of the pen, as under Hardy-Weinberg equilibrium it should be p = 2root-uv. In fact, I now find that this error was listed in the printed Corrigenda to the relevant volume of Genetics but has not been corrected in the pdf copy.] Systems of Mating I I will conclude this note with some comments on Wright's most important paper on the subject: the first in the series on Systems of Mating (SM1). Here Wright uses his method of path analysis to derive the correlation between relatives. In principle the ultimate result is a correlation between phenotypes, which should take account of all environmental and genetic influences, including dominance, epistasis, assortative mating, and shared environment (if any). While the method of path analysis has some advantages for this purpose, which Wright emphasised, it also has some disadvantages. The variability among individuals is partly due to the chance effects of genetic recombination and segregation. It is therefore necessary for the path diagrams to contain an independent variable designated as 'chance' (see the diagram in SM1, p.116), which may be formally justified but still looks odd. More importantly, the method of path analysis assumes that the effects of causal influences can be simply added together. In genetics this is not always the case, as the effects of epistasis and dominance are not purely additive. Wright therefore excludes epistasis from his model 'for the present' (p.117). He does attempt to incorporate an adjustment for the effects of dominance, but this is not entirely successful. For the time being I will assume that the method is confined to the additive effects of genes. It is not always clear what is the relevant population for the purposes of the correlations, especially as more than one generation of individuals are often involved in the correlations. Wright seems to assume (see the beginning of SM4) that in the absence of selection the proportions of different alleles in the total population will be constant, but in a finite population this cannot be strictly true, as there will be fluctuation due to genetic drift. Perhaps Wright is assuming for the purpose that the population can be regarded as indefinitely large. In this case it is legitimate to assume that gene frequencies in the absence of selection are constant. More seriously, it is not clear whether the intended reference population is the current population of each generation, the 'foundation stock' from which they are descended, or some combination of the two. Wright's reference to 'random mating' at the top of page 119 of SM1 would not make much sense if the intended reference population is the current one (of the parents), since f' would then always be zero. Each path of descent is built up from the links between parent and offspring, so this relationship is especially important. In Wright's analysis (page 118-20) the direct relationship between parent and offspring can be analysed as a path with the following steps: parent's phenotype - parent's genotype - gamete (egg or sperm) - offspring's genotype - offspring's phenotype. (If the offspring's two parents have a non-zero correlation, an indirect path via the other parent also needs to be considered.) The path coefficients along the direct path from parent to offspring can be represented in the form hbah, where h represents the correlations between the phenotypes and genotypes of the parent and offspring (which may be different). The correlation coefficient can be considered a measure of broad heritability, that is, the extent to which the individual's phenotype is determined by the genotype. Its square, h^2, measures the proportion of phenotypic variance accounted for by genetic variance. This is historically the origin of the familiar use of h^2 to represent heritability. It should however be noted that Wright's usage is not quite the same as the modern one. In modern usage h^2 usually stands for narrow or additive heritability, measured by the extent to which the offspring predictably resemble the parents. Wright's h^2 is closer to the modern concept of broad heritability, as it measures the extent to which the phenotype of an individual is determined by its genotype. The key equation (p.116) is h^2 + d^2 + e^2 = 1, where h stands for all aspects of genetic heredity, and e and d stand for predictable effects of the environment and random fluctuations in development. The coefficients a and b are the path coefficients representing, respectively, the contribution of the gamete (egg or sperm) to the variance in the genotype of the offspring, and the contribution of the parental genotype to the variance in the gametes. As none of these entities have a measurable phenotypic value, it is necessary to assume that they have arbitrary algebraic or numerical values, in the way discussed above. Wright's derivation of the values of a and b (SM1, pp.118-19) is particularly important, and needs to be carefully studied. Unfortunately it is not easy to follow. I would offer two tips. First, it is essential to refer frequently to the path diagram on page 116, without which the derivation would be unintelligible. Second, Wright does not explain why pG.H'' = rG.H'', which is crucial to the validity of the proof. I think it follows from the fact that the only causal path from the parental genotype to the gamete is the direct path pG.H''. [Added: having written this, I am pleased to find that Wright gives this explanation in another article.] It should be noted that if the parents are unrelated and not inbred, a and b are both equal to root-1/2, so the product ab along the path from parent to offspring in this case equals one-half, as in Malecot's method. It may perhaps be felt that Wright's derivation of the path coefficient b is a trick with smoke and mirrors. It is mathematically valid, but Wright's claim that 'in a sense, it is legitimate to reverse the arrows....' invites the response that in another sense it is not legitimate, since there is no causal influence from the gametes back to the gametocyte. This part of the proof therefore goes against the spirit if not the mathematical letter of path analysis. At the top of page 120 Wright explains, very terseley, how correlations between relatives can be derived from the path coefficients. Again, it should be noted that in simple cases, and with perfect additive heritability, the results are the same as Malecot's. Wright then attempts to take account of dominance. As noted above, on page 117-8 of SM1 Wright gives formulae for the correlation between genotypic values with and without dominance. In the standard case of random mating the correlation comes out at root-1/1+p, where p is the proportion of heterozygotes in the population. To adjust the correlations between relatives to allow for dominance, Wright multiplies them by 1/1+p. He does not explain the logic behind this, but I think it is that each of the two correlated relatives has a genotypic value without dominance, which is the basis for the original correlation, and that these values can each be multiplied by root-1/1+p to give a typical adjusted correlation between the values with dominance. The effect is to reduce the correlation between the individuals by the factor 1/1+p. It may perhaps be wondered why only the two individuals at each end of the chain, and not the intermediate individuals, have their values adjusted. I think the explanation is that dominance is essentially an effect on phenotypes rather than genotypes, and in calculating the correlation between the individuals at the ends of the chain we need not take account of dominance effects on intermediate phenotypes any more than we need take account of environmental effects on them, since these do not affect the path coefficients along the chain. Unfortunately Wright discovered, after reading Fisher's 1918 paper, that except in the case of half-siblings his own treatment of dominance effects was invalid, and in a footnote to his famous 1931 paper on 'Evolution in Mendelian Populations' he withdrew it. His original method therefore never satisfactorily covered epistasis and dominance. He later attempted to incorporate a revised treatment of dominance in his method of path analysis, but the result was very complicated. [See EGP vol 2., p435-6.] In this area Fisher's Analysis of Variance has been more generally used. The method of path diagrams remains very useful for the analysis of relationships, but the paths are now usually interpreted in Malecot's fashion as probabilities of Identity by Descent, and not as correlations. The Problem of Negative and Zero Correlations I emphasised earlier that in Wright's system the correlations between relatives, and therefore the measures of relatedness, can be zero or even negative. Yet it seems that Wright's actual procedures for measuring relatedness, by tracing path coefficients back through common ancestors, can only produce positive figures. For example, suppose that on average two randomly chosen members of a population have a degree of relatedness, measured by Identity of Descent within, say, the last thousand years, equivalent to that of full first cousins, i.e. a Malecot Coefficient of Relationship of one-eighth. On the face of it, if we trace back the paths of descent using Wright's methods, and work out the path coefficients, assuming complete additive heritability, the result will be a correlation of one-eighth, numerically equivalent to the Malecot coefficient. But the correlation coefficient between randomly selected members of a population, relative to that population as a whole, must be approximately zero. We therefore seem to have a contradiction. It took me a while to see how this paradox can be resolved. I think the main explanation [see Note] is that in the usual applications of Wright's methods there is a tacit assumption that only the paths leading through common ancestors need be taken into account. All other paths can be regarded merely as background noise. For example, if we trace the paths between two full first cousins, we need only take into account the paths leading through the two grandparents they have in common, and not the other four grandparents, unless some of these lead back to other common ancestors in the fairly recent past. Ordinarily this is a reasonable approach, but it breaks down if it is is applied to the kind of case referred to in the last paragraph. If we trace back the entire ancestry of two randomly chosen individuals, for some large number of generations, the ancestors will have a mixture of positively and negative correlations between them. The positive and negative correlations will (approximately) cancel out. In a complete path analysis all these correlations would need to be taken into account, even if they do not involve a direct path through a common ancestor. When properly interpreted, Wright's methods therefore do not lead to a contradiction. I had originally planned to go on to consider the extension of Wright's measures of kinship to the relations between populations, such as his well-known FST statistic. But the post is already long, so I will reserve the subject for another time. Note: I say the main explanation , because the effect of common ancestry itself may also be reduced when we take account of negative correlations. For example, in the case of cousins with two common grandparents, these two grandparents may be negatively correlated, in which case the indirect path running through both of them would have a negative value. Or a common ancestor might have a negative coefficient of inbreeding (i.e. be less inbred than average for the population), which would reduce the path coefficient from parental genotype to gamete. But as far as I can see, these factors would never be sufficient to offset the positive correlations due to common ancestry entirely. It is therefore also necessary to take account of negative correlations between non-common ancestors. Labels: Burbridge, Genetics, Population genetics
Saturday, March 15, 2008
A long time ago I said I was planning a series of posts on the work of Sewall Wright. I am finally getting round to it.
I originally planned to write notes on the following topics: 1. The measurement of kinship. 2. Inbreeding and the decline of genetic variance. 3. Population size and migration. 4. The adaptive landscape. 5. The shifting balance theory of evolution. I still hope to cover these topics, but I will begin with a few notes on Wright's method of Path Analysis..... Path Analysis is Wright's main contribution to statistical theory. It is one of several methods of multivariate analysis developed between 1900 and 1930, after the basic theory of multivariate correlation and regression had been established by Karl Pearson and others in the 1890s. Other types of multivariate analysis include Factor Analysis, pioneered by the psychologist Charles Spearman in 1904; Principal Component Analysis, developed by H. Hotelling in the 1920s but foreshadowed by Karl Pearson in 1901; and Analysis of Variance, due mainly to R. A. Fisher from 1918 onwards. A bibliography of Wright's main work on Path Analysis is available here. The three most useful items are: 1. Correlation and causation (1921) 2. The theory of path coefficients: reply to Niles's criticism (1922) 3. The method of path coefficients (1934) Items 1 and 3 are available as pdf downloads linked to the online bibliography. Item 2 is not, but it is available here. As I mentioned in a previous post, a page is missing from the pdf file of item 1, but fortunately the most important part of the missing page (the definition of path coefficients) is quoted verbatim in item 2. The distinctive feature of Wright's path analysis is that it introduces questions of causation into the treatment of correlation and regression between variables. Every statistics textbook makes a ritual statement that 'correlation does not imply causation', but in practice there very often is a causal relationship between correlated variables. Path Analysis provides a systematic means of investigating such relationships. As Wright several times emphasised, it does not provide a method of discovering or proving causal relationships, but if these are known or hypothesised to exist on other grounds, Path Analysis can (in principle) help quantify their relative importance. The following comments are in no way intended as a substitute for reading Wright's own studies, which are essential. I am only aiming to provide supplementary explanations on points which Wright deals with very briefly, and sometimes obscurely. In particular, I want to clarify the relationship between Path Analysis and multivariate correlation and regression. Wright's own attitude on this seems to have changed over time. It seems that initially he was dissatisfied with what he thought of as paradoxes in the existing methods, and wanted to provide a substantially different approach. But in the course of his work he discovered that his own system was more closely related to conventional multiple regression than he had realised, and increasingly he emphasised this relationship. In Path Analysis the investigator first devises a model, shown in a path diagram, representing the assumed direction of causal relationships among a number of variables. There will be one or more dependent variables, and one or more independent variables which are assumed to influence the former. Some variables may be intermediate links in a chain of causation. The independent variables may be either correlated or uncorrelated with each other. Each segment of a path in the diagram is assigned a path coefficient which quantitatively measures the strength of the causal influence along that segment. The fundamental problems in understanding Path Analysis are: what exactly are these path coefficients? And how are they to be quantified? I will return to these questions shortly. Assuming for the moment that all the path coefficients are known, the correlations between the variables can be derived from the path coefficients by a few simple rules. Briefly, the correlation between any two variables is the sum of the products of the path coefficients along each distinct path (or chain of paths) joining the two variables. For this purpose a correlation between two independent variables can be counted as a path between them. The relative importance of the causal influence of an independent variable on any given dependent variable can be measured by the square of the path coefficient between them, which Wright calls a 'coefficient of determination' (possibly the first use of this term). The rules for operating with path coefficients are explained by Wright reasonably clearly in 'Correlation and causation' and later papers. [Note 1] The real difficulty is to understand the nature of the path coefficients themselves. Wright's verbal explanation is that 'the direct influence along a given path can be measured by the standard deviation remaining in the effect after all other possible paths of influence are eliminated, while variation of the causes back of the given path is kept as great as ever, regardless of their relations to the other variables which have been made constant.' This is defined as 'the standard deviation due to' the independent variable in question. The path coefficient itself is then defined as the ratio of this standard deviation to the total standard deviation of the dependent variable. This definition is not ideally clear, especially for cases where the independent variables are correlated with each other. Various objections were made in a critique of Wright's theory by Henry Niles. In his 'Reply to Niles' Wright admits that 'the operations suggested by the verbal definitions could not be literally carried out in extreme cases, and the definition is therefore imperfect'. Wright points out, however, that the path coefficient can always be calculated by the methods described in his 1921 paper. In the later paper on 'The method of path coefficients' Wright offers a variant on his original definition which is perhaps a little clearer: 'Each [path coefficient] obviously measures the fraction of the standard deviation of the dependent variable (with the appropriate sign) for which the designated factor is directly responsible, in the sense of the fraction which would be found if this factor varies to the same extent as in the observed data while all others .... are constant'. The problem with both formulations, as Wright was aware, is that in the case of correlated independent variables they seem to require a counterfactual assumption. If all variables other than the dependent and independent variables of interest are held constant, but one or more of those other variables are correlated with both of the variables of interest, then both of the latter variables will have their variability reduced. By insisting that the causative variable of interest retains its full variability, Wright is therefore assuming a counterfactual condition. In order to keep the variability of the causative variable unchanged, Wright says 'the definition of [the standard deviation in X due to M] implies that not only is [the other independent variable] made constant but that there is such a readjustment among the more remote causes .... that [the standard deviation of M] is unchanged ('Correlation and Causation', p.566). What Wright meant by 'readjustment' is unclear to me and, so far as I know, Wright never attempted to explain it. The causal relationships are what they are, and any 'readjustment' sounds like an artificial if not improper procedure. Rather than make further efforts to decipher Wright's formulations, I think it will be more useful to approach the problem from first principles, drawing on the general theory of correlation and regression as set out in my Notes on Correlation, Parts 1, 2, and 3. I hope to show that Wright's path coefficients can in fact be derived in a way which avoids the problems of his verbal formulations. I will assume linearity of all relationships. (Wright also in general assumes linearity, but does briefly consider the effects of departures from linearity.) It is presupposed, of course, that items represented by one variable are associated in some way with the items represented by the other variables, e.g. that the height of fathers is associated with the height of sons. The general idea behind Wright's definition is that variation in one (independent) variable has an effect in producing variation in another (dependent) variable. Since we are assuming linearity, the size of the effect should be simply proportional to the size of the cause. This naturally suggests a connection with statistical regression. The regression of one variable on another measures the average size of the deviation in the dependent variable as a proportion of the associated deviation in the independent variable. In the case of a causal influence, it is therefore reasonable to say that a certain amount of variation in one variable is caused by or 'due to' its regression on the other. The effects caused in this way will have a calculable standard deviation, which can be taken as a measure of the total size of the causal influence. Case 1 Let us begin with the simplest possible case. Suppose there is one dependent variable, X, and one independent variable, Y. I assume, as usual, that the variables are measured as deviations from their means, in appropriate units (not necessarily the same for both variables). Let the regression coefficient of X on Y be designated bxy. We are assuming that each unit of variation in the items of Y has a simple proportional effect on the corresponding items in X. The proportion must then be equal to bxy, since this is a measure of the proportional mean deviation in X associated with a given deviation in Y. For example, if bxy = .6, then for each deviation of 1 unit in Y there will on average be a deviation of .6 units in X. In general this need not be a causal relationship, but in the present case we are assuming that it is, and that the deviation in X is an effect 'due to' the deviation in Y. The total amount of variation in X that is due to variation in Y will of course depend on the total amount of variation in Y as well as on the regression coefficient. If we designate the standard deviation of Y as sy, the standard deviation in X that can be attributed to the causal influence of Y will be bxy.sy. [Note 2] If the total standard deviation of X is sx, the proportion of the standard deviation of X that is due to Y will therefore be bxy.sy/sx. But this equal to the correlation coefficient between X and Y. We therefore find that in this simple case the path coefficient between X and Y equals the correlation coefficient between them. Case 2 Turning to a slightly more complex case, let us suppose that Y influences X via an intermediate variable Z, and that Y is uncorrelated with any other variables in the system. Each unit deviation in Y will produce a deviation of bzy in Z, and in turn each unit deviation in Z will produce a deviation of bxz in X. The indirect influence of Y on X through Z will therefore be equal to the product bzy.bxz. Since by assumption there is no other path of influence of Y on X, the product byz.bzx will measure the total influence of each unit deviation of Y on Z. The standard deviation in X due to Y will be byz.bz.sy, which as a proportion of the total standard deviation in X is bzy.bxz.sy/sx. On a little examination it can be seen that this is equal to ryz.rxz, which we may call the compound path coefficient between X and Y. But by the arguments of the previous paragraph, the path coefficient between Z and X will be rxz and that between Y and Z will be ryz. The product of the path coefficients between Y and Z and Z and X is therefore ryz.rxz, which is the same as the compound path coefficient between X and Y. It may also be noted that if the sole influence of Y on X is via Z, the partial correlation coefficient between X and Y given Z should be zero, which implies rxy = ryz.rxz. The compound path coefficient between X and Y is therefore the same as rxy, the bivariate correlation between them. Case 3 The last conclusion can also be applied to the case of a single independent variable Z which affects two dependent variables X and Y. If Z is the only reason for correlation between X and Y, the partial correlation coefficient between X and Y given Z will be zero, which implies rxy = ryz.rxz. But ryz and rxz are also the path coefficients between Y and Z and Z and X, so the compound path coefficients between X and Y is the same as the correlation between them. Case 4 Suppose now that we have two dependent variables, X and Y, and two independent variables, A and B, which are uncorrelated with each other. This gives us two 'paths' between X and Y. Each of these paths can be considered as an example of case 3, so that they will each give an estimate for the correlation between X and Y. The problem is, how can the two estimates be combined? Since A and B are uncorrelated, a plausible guess is that the two estimates should simply be added together. This can be proved more rigorously using the formulae for partial correlation, as is done by Wright ('Correlation and Causation', p.565). The argument can easily be extended to cases with more than two independent variables. The result is that if all the independent variables are uncorrelated with each other, the correlation between two variables is equal to the sum of the products of the correlations along all paths connecting the two variables. Case 5 We have so far assumed that the independent variables are all uncorrelated with each other. Things get more complicated when two or more of the independent variables are correlated (including the case where two 'intermediate' variables lead back to the same independent variable, and are therefore correlated with each other). If we have dependent variables X and Y, and correlated independent variables A and C, the total correlations between X (or Y) and A will be partly attributable to A's correlation with C. [I am avoiding using B to designate variables, as I use it to designate partial regression coefficients.] If we simply added the correlations resulting from the paths X-A-Y and X-C-Y, as in case 4, the correlation between X and Y would be inflated by double-counting, and could well be greater than 1 or less than -1, which is impossible. These considerations suggest that the correlations between a dependent variable and the independent variables cannot in themselves give us the required path coefficients. But this does not tell us what the path coefficients should be, or even guarantee that any suitable measure for the purpose exists. Drawing on the theory of multiple regression and correlation, as developed in Notes Part 3, an alternative measure does suggest itself. It was pointed out there that the partial regression coefficient of X on Y, given Z, measures the independent contribution of Y to the best estimate of X, when Z is held constant. Surprisingly, the partial regression coefficient can serve a dual purpose. When multiplied by the full deviation of the relevant independent variable, it contributes to the best estimate of the value of the dependent variable as given by a multiple regression equation. When multiplied by the residual deviation of the relevant independent variable, after subtracting the estimate derived from the regression on the other independent variable, it gives the best estimate of the residual deviation of the dependent variable. It is not intuitively obvious that the same coefficient can serve these two different purposes, but it is demonstrably the case. Wright's concern about the restricted variability of the independent variable, and the need to 'readjust the more remote causes', therefore seems unnecessary. If we take the partial regression coefficient Bxa.c, (see Notes Part 3 for this notation) and multiply it by the full deviation value of A, this should itself be a suitable measure of the independent causal influence of A on X, taking account of C. The standard deviation of the effect of A on X will then be (Bxa.c)sa, which as a proportion of the total standard deviation in X will be (Bxa.c)sa/sx. But this is equivalent to the Beta weight of X on A, given C. (See Notes Part 3.) The suggested value for the path coefficient is therefore equal to the relevant Beta weight. If the variables are measured in units of their own standard deviations, as Wright recommends for most purposes, the partial regression coefficients and Beta weights will coincide. This is the same as Wright's result, but reached via the theory of multiple regression. By Wright's own account, he did not originally take this approach, and was surprised when late in his investigation of the problem he realised the close connection between path coefficients and multiple regression. (See 'Reply to Niles', p.242.) I would suggest that it would be better to explain Path Analysis from the outset as a 'causalised' version of multiple regression. The other main question in Path Analysis is how to quantify the path coefficients. If all the correlations between the variables in the system are known (or hypothesised), then the path coefficients can be calculated by using in reverse the rules which enable the correlations to be derived from the path coefficients. (This will sometimes require simultaneous equations, but there should be enough equations to determine the unknowns.) If there are gaps in the available information, these may often be filled by imposing the condition that the 'coefficients of determination' for each variable must, if the scheme of causation is complete, collectively account for the total variance of the variable. Wright also often makes use of the principle that the correlation of a variable with itself is 1. Overall, Wright's method of Path Analysis is a very impressive achievement. It is interesting to note that two of the major methods of multivariate analysis devised in the 20th century were the work of people who were only amateurs in statistics (the other example being Spearman's Factor Analysis). Despite the scale of Wright's achievement, Path Analysis never seems to have received the same general acceptance as Fisher's Analysis of Variance. For example, it is seldom covered in general textbooks on statistical methods. It seems to have had occasional phases of fashionability in particular fields, notably in sociology, without ever quite becoming part of standard statistical practice. (Incidentally, Wright himself criticised some of the uses it was put to in the social sciences, which can hardly have encouraged would-be practitioners of the method.) Probably one reason for its unpopularity is that Wright's method requires the use of diagrams. Perhaps more important in modern times, it resists reduction to off-the-shelf computerisation. It is impossible to do Path Analysis without a human brain. But it may also be wondered whether Path Analysis has quite justified Wright's hope that it would help clarify causal relationships. Wright himself used it mainly for the narrower purpose of calculating genetic relatedness, where the nature and direction of causal influences is unambiguous. This is seldom the case in other fields. (And even in this field his methods have largely been superseded by Malecot's concept of Identity by Descent, which uses diagrams which look like an application of Path Analysis but are conceptually quite different.) It seems also that Wright was originally motivated by a belief that the existing methods of multiple regression and correlation were inadequate or paradoxical, and needed to be supplemented. But in the process of working out his method, he discovered that it was more closely related to multiple regression than he had realised at the outset. The 'added value' of Path Analysis as compared with other methods may therefore not always justify the extra effort involved in mastering and applying the technique. Postscript: Since writing this I have found a useful explanation and evaluation of Path Analysis in an article by O. D. Duncan, 'Path Analysis: Sociological Examples', American Journal of Sociology, 72, 1966, 1-16. Another, more technical, account is given by K. C. Land in 'Principles of Path Analysis', Sociological Methodology, 1, 1969, 3-37. Both articles are available on JSTOR for those with access. Note 1: One relatively obscure point is Wright's discussion of the correlation of a variable with itself, which must equal 1. Although Wright discusses this case on several occasions, I do not think he ever gives a path diagram for it, or explains how it would be drawn. I think the best way of doing it would be to insert the self-correlated variable in the diagram twice, perhaps labelled X(1) and X(2). Note 2: For any given deviation value of Y, the associated deviation value of X will be bxy.Y. The total of the deviations due to Y will be S(bxy.Y), with the summation taken over all values of Y. Since SY is a sum of deviation values, S(bxy.Y) equals zero, but the sum of squares, S(bxy.Y)^2, will in general be non-zero. The standard deviation in X due to Y will be root-[S((bxy.Y)^2)/N]. But root-[S((bxy.Y)^2)/N] = bxy.[(root-SY^2)/N]. The expression in square brackets is the standard deviation of Y, so abbreviating this as sy we have shown that the standard deviation in X due to Y is equal to bxy.sy. Labels: Burbridge, Population genetics
Saturday, February 23, 2008
A recent article by D. S. and E. O. Wilson [1] has been acclaimed by some as reviving the fortunes of group selection. It must for a time have been available on the web (since I downloaded a pdf of the published version a month or so ago), but the closest thing I can find at present is this slightly different version submitted to (and presumably rejected by) Science in 2006. [Added: I should perhaps have mentioned that the two Wilsons are not related. No kin selection here!]
As gnxp's resident critic of group selection I feel an obligation to say something about the article, but I find the task dispiriting. Much of the Wilsons' article is a re-working of issues which have been debated many times before. (See e.g. my discussion here.) The debate has been largely about the most useful way of describing and classifying the phenomena, rather than about the biological facts. Hostility to group selectionism is provoked in part by the tendency of its advocates to claim for group selection a range of phenomena that other biologists regard as more usefully described in terms of inclusive fitness (kin selection). This hostility will not be allayed by such prominent assertions as: During evolution by natural selection, a heritable trait that increases the fitness of others in the group (or the group as a whole) at the expense of the individual possessing the trait will decline in frequency within the group. If the 'group' contains local concentrations of relatives (as it very often will), or if the trait preferentially affects relatives, this assertion is simply not correct. Did the Wilsons not notice this, or were they deliberately loading the dice against interpretations in terms of kin selection? Another potential confusion of the issues comes later in the article, where the Wilsons discuss insect eusociality. They argue strongly that between-colony selection is important in the evolution of eusocial insects, for example in traits such as nest construction. But whoever doubted it? Once eusociality (specialisation of reproduction) has been established, of course genetic variation and selection will often be between different colonies. The difficult question is how eusociality itself becomes established. The important insights into this have come from inclusive fitness theory, not group selectionism. (See for example chapter 11 of [2].) Rather than spend more time on arid and abstract theoretical issues, I think it will be more rewarding to focus on a single empirical case, which the Wilsons themselves offer as a good example of the benefits of a multi-level approach. It can therefore serve as a test case of the benefits of that approach. The example I have chosen is the Wrinkly Spreader... As the Wilsons describe this case, the "wrinkly spreader" (WS) strain of Pseudomonas fluorescens evolves in response to anoxic conditions in unmixed liquid medium, by producing a cellulosic polymer that forms a mat on the surface. The polymer is expensive to produce, which means that non-producing 'cheaters' have the highest relative fitness within the group. As they spread, the mat deteriorates and eventually sinks to the bottom. WS is maintained in the total population by between-group selection, despite its selective disadvantage within groups, exactly as envisioned by multi-level selection theory. I have followed up the Wilsons' reference for this case, and then some other citations. [Refs. 3, 4, and 5] The facts of the WS case (stripped of theoretical baggage) seem to be as follows. Pseudomonas fluorescens is a rod-shaped flagellated aerobic bacterium. It is found widely in the soil and in fresh water. In nature it is normally found as a single free-moving cell. In laboratory cultures, on the other hand, it often develops mutant strains which stick together rather than living singly. One of these is the Wrinkly Spreader strain, so-called because on slides of nutrient jelly it spreads out in sheets with a distinctive wrinkly appearance. In open containers (e.g. test tubes) of nutrient fluid the WS bacteria form a mat on the surface. Within about 10 days the mat becomes too heavy and sinks to the bottom. If the supply of nutrient is adequate, the process may be repeated, with new WS mats forming and eventually sinking. Rainey and colleagues have studied the genetics of the WS strain.[3, 4 and 5] They have found that WS bacteria produce an excess of a cellulosic polymer which causes them to stick to each other and to surfaces. A side-effect of this is that they form a scum at the liquid-air interface (I presume this is a surface-tension effect, but the precise mechanism does not matter.) The production of the polymer uses scarce resources, so WS bacteria reproduce more slowly than non-WS bacteria in the same circumstances. However, this is offset by the advantage of being able to colonise the surface layer, with its better access to oxygen. The description so far assumes that the mats on the surface contain only WS bacteria, usually derived from a single mutant individual. WS bacteria within the mat may however mutate in various ways which stop them overproducing the polymer, so that they revert to the ancestral phenotype. These mutants reproduce more quickly than the WS strain. They therefore tend to spread within the mats. But this weakens the structural integrity of the mats, which causes them to break up and sink more rapidly than the pure WS mats. So what has this to do with group selection? What are the 'groups', and where is the 'selection'? I think it will help to divide the cycle into two stages: before and after the emergence of non-WS mutants within the mats. At the beginning of the process, there are only single bacteria. Some of these mutate to the WS form, and literally stick together. Within the broth culture as a whole, WS mutants have lower fitness than the ancestral form, but the mutation gives them characteristics which enable them to predominate in a particular part of the ecosystem, i.e. the surface layer. Rainey et al. describe this as a form of 'cooperation', in which 'cooperation is costly to individuals, but beneficial to the group'. They note that the WS individuals are closely related (since they are descended from the same mutant individual) and describe the trait as spreading by 'kin selection'. This seems to me an unnecessary interpretation. The WS individuals in the surface layer are not sacrificing any fitness for the benefit of other individuals: they are simply using resources in a way that enables them to occupy this part of the environment. In a heterogeneous environment it can be misleading to average fitness over the entire range of sub-environments. For analogy, suppose a species of sheep ranges over a variety of altitudes. At higher altitudes the climate is colder, and the sheep need thicker fleece to live there in the winter. Sheep with mutations causing them to grow thicker fleece may have lower fitness than the average sheep, because it is costly to grow thick fleece, but at high altitudes the thick-fleeced variant may predominate because it is better adapted to that particular environment. Similarly, the WS strain is better-adapted to the surface layer. It is merely a coincidence that the adaptation involves the formation of 'groups'. We could imagine that instead of producing a polymer, and sticking together, the mutants produced little bubbles of gas which enabled them to float at the surface. In this case, no-one would dream of describing the process as either kin or group selection. There is a more plausible case for appealing to group selection in the later stage of the process, when non-WS individuals have emerged within the WS mats. These individuals obtain the advantage of living in the surface layer without paying the cost. It is therefore reasonable to describe them as 'cheaters' or 'defectors'. They reproduce more rapidly, for a while, but in the longer term destroy the mats, to the detriment of all. According to the Wilsons, 'WS is maintained in the total population by between-group selection, despite its selective disadvantage within groups, exactly as envisioned by multi-level selection theory.' This is one possible interpretation of the facts, but it seems to me to go beyond the evidence presented by Rainey et al. We should note (as the Wilsons do not) that all surface mats collapse within a few days, whether or not they contain defectors. The regeneration of surface mats then depends on the establishment of a new population of WS individuals at the surface. These could emerge either by new mutations from the ancestral form, or from fragments of the collapsing WS mats. (It is not clear from the papers I have seen which of these usually occurs.) Either way, the Wilsons' description is incomplete. It implies that some WS 'groups' (the ones without defectors) survive indefinitely, while others fail. This is not the case. Even if a description in terms of group selection is formally valid, it does not (in my opinion) add much of value to the understanding of the phenomena. And if this is one of the best examples of group selection that its advocates can find, one cannot have much confidence in the others. (And indeed, some of the others, like the Wilsons' reference to the territorial behaviour of female lions, seem even worse. How can anyone sensibly discuss this without mentioning that the lionesses of a pride are usually closely related? [6, p. 37]) This is not to say that an account in terms of group selection will never provide useful insights into evolutionary processes. The evolution of disease organisms such as Myxomatosis seems to be one very plausible example. But the Wilsons' article does not persuade me that group selection, as distinct from inclusive fitness, is more than a minor wrinkle on the face of evolutionary theory. References: [1] D. S. and E. O. Wilson: 'Rethinking the Theoretical Foundation of Sociobiology', Quarterly Review of Biology, December 2007, vol. 82. No.4, 327-348. [2] J. Maynard Smith and E. Szathmary: The Origins of Life: from the birth of life to the origins of language, 1999 [3] P. B. and K. Rainey: 'Evolution of cooperation and conflict in experimental bacterial populations', Nature, 425, 2003, 72-4. [4 P. B. and K. Rainey: 'Adaptive radiation in a heterogeneous environment', Nature, 394, 1998, 69-72. [5] A. J. Spiers et al.: 'Adaptive divergence in experimental populations of Pseudomonas fluorescens. I: Genetic and phenotypic bases of Wrinkly Spreader fitness', Genetics, 161, 2002, 33-46. [6] G. B. Schaller: The Serengeti Lion, 1972. Labels: Burbridge, Genetics, Population genetics
Monday, February 04, 2008
I and others at this site have written much about recent human evolution, with a particular emphasis on papers that have used large-scale genotyping data on individuals from diverse populations to make inferences about regions of the genome that appear to be under natural selection. The sources of information used by these papers vary, and the logical chain from the observation to the inference of selection might be difficult for a non-specialist to follow.
So it's nice to be able to clearly state the logic behind a new paper scanning the genome for evidence of the action of natural selection: if an allele is at really high frequency in one population and really low frequency in another, that's interesting. To go into a slight bit more detail, the authors use the HapMap, a database of genotypes at >3 million SNPs individuals of East Asian, African, and European descent, and calculate Fst, a measure of how different allele frequencies are between the three broad continental groups. They hypothesize that, assuming population differentiation is driven by natural selection and not genetic drift, the most extreme SNPs should then be enriched for genic regions (as opposed to non-genic regions) and non-synonymous SNPs (as opposed to synonymous SNPs).  On the right is the moneymaker, showing exactly that--high Fst SNPs (ie. towards the right of the graphs) are enriched for both genic and non-synonymous SNPs. Interestingly, SNPs in the 5' untranslated region of genes are also highly differentiated, suggesting perhaps some role for gene regulation through microRNAs in recent human adaptations.  The authors compile a list of the genes most highly differentiated between the three human populations included in their study (also on the right), including many of the known suspects, including EDAR and SLC24A5. To me, the striking thing is the huge list of genes of unknown function--it's always humbling to realize how little is known about human biology. Humbling and of course exciting--someone's going to figure out what these genes do, and this study suggests at least some of the them play large roles in determining what makes human populations so diverse. Something to watch for... Labels: Genetics, Population genetics
Thursday, January 31, 2008
It's like shark week, only better! Whet your appetite with "High-Resolution Mapping of Crossovers Reveals Extensive Variation in Fine-Scale Recombination Patterns Among Humans", then top it off with "Sequence Variants in the RNF212 Gene Associate with Genomewide Recombination Rate". Enjoy!
Labels: Association, Genetics, Population genetics
Sunday, January 20, 2008
From here:
 Each point is an individual, and the axes are the first two principal components of "genetic space". Colors correspond to individuals of different European ancestry. Each point is an individual, and the axes are the first two principal components of "genetic space". Colors correspond to individuals of different European ancestry.Labels: Population genetics
Monday, January 14, 2008
Back in the days before I'd ever read any probability or population genetics, I imagine I considered, as many laymen still do, evolution as a sort of deterministic march towards some optimum. I still remember being amazed at the simple equations that show how much stochasticity is involved; how random chance and historical accident can shape the fate of genetic variants. But are there cases where the layman's instinct is correct, where we can say that evolution was deterministic? Obviously, in some sense this is impossible to prove; one can't simply rewind the clock a thousand times and watch the outcomes. But there are natural experiments that I think shed some light on the subject.
The advent of dairy cultures in various human populations around the world provides one such natural experiment. I'm writing about this because of a recent study identifying yet another allele leading to lactose tolerance, this time in a Saudi Arabian population that drinks sheep's milk. A previous study, regular readers may remember, identified three other polymorphisms leading to the phenotype in Sub-Saharan pastoralists. Along with the "European" allele, this brings the total of probable lactose-tolerance-causing mutations segregating in humans to five. Let's make some assumptions: lactose tolerance is perfectly dominant, has a selection coefficient of around 0.1, and all these mutations will continue to fixation (this last one would be almost certainly true if the selection coefficient were constant--all the alleles have escaped the stochastic phases of their trajectories--but is an open question. What is the fitness advantage today of lactose tolerance? Surely this is testable). With these assumptions, one predicts that lactose tolerance has arisen around 25 times since it became advantageous. Given that we're talking about less than ten thousand years since dairy farming, that's quite remarkable. The relevant parameter here is the mutational target size--if lactose tolerance could only be caused by a change at one particular base pair in humans, it would never have arisen independently so many times. But with a mutational target so large, and a selection coefficient so strong, it becomes inevitable that any culture that developed dairy farming would eventually develop lactose tolerance. But it still seems amazing to me that it happened so quickly! Labels: Genetics, Human Evolution, Population genetics
Saturday, December 22, 2007
As background to a couple previous posts where I made somewhat technical comments about simulations in population genetics, I was in the middle of writing a rather lengthy primer on coalescent theory. Then I saw that RPM has an old post pointing to some of the same material I was planning on hitting. So instead I'll just say read his post and the links therein. I may get around to finishing what I was writing (there's a bit of math that most people don't care to see, so maybe not), but you can essentially boil it down to RPM's last point:
Without a null model based on the coalescent, there is no way to statistically test hypotheses that are based on DNA data, regarding things like population structure.Or natural selection. Labels: Population genetics
Thursday, October 25, 2007
Back when this blog was young and its was age measured in months, not years, "godless capitalist" (gc) would debate Paul Orwin and Charles Murtaugh, especially on the issue of QTLs which affect normal variation in IQ. When gc made the case for possible genetic engineering of one's offspring to have higher IQs Murtaugh was aghast. His basic logic seemed to be that the QTLs which contribute to normal variation in IQ are of small effect, so there are many, and who knows what sorts of problems might be caused by "switching" dozens of genes from state A to B? Genes are often of course pleiotropic, and Murtaugh's assumption seemed to be that changing the genetic architecture in such a profound way might not be a good thing in the genetic background of the typical human. We're a species with a very high rate of spontaneous abortion, perhaps as much as 3/4 of fertilizations do not come to term. Much of this is likely due to chromosomal abnormalities, but there are likely other factors as well, so let's take Murtaugh's objection seriously for a minute.
What sort of superior child do most parents which frank eugenic inclinations want? Wouldn't you want your son to be both tall and extremely intelligent? For example, a male who is 1 standard deviation taller than the norm and 2 standard deviations more intelligent would be at a relatively advantage in life. But the chances of having a tall Mensa level IQ son is not high for most humans, and even if you assume some dependence of the deviation of one trait conditioned upon other, that dependence is likely still relatively weak. Finally, both of these are quantitative traits where the average effect from a given gene seems small in their contribution to normal human variation. The right flavor of HMGA2 gives you 1 extra centimeter, but that really isn't that much, and this is likely a QTL of very large effect for this trait (height). For intelligence the prospects may even be weaker. To engineer a very tall and intelligent son if you are of normal intelligence & height (the typical future consumers) would require alterations on many loci, and this is where Murtaugh might pipe up with cautionary tales. But then I thought of something: there are other traits where most of the variation seems associated with a few loci of large effect. Europeans' light skin is in large part due to SLC24A5, SLC45A2, TYR and OCA2. 4-6 loci probably account for around 90% of the variation. What about eye color? OCA2 is responsible for 3/4 of the variation, with TYR rounding out much of the balance. Skin color, eye color, even hair color; these are gross outward phenotypes controlled by a few loci of large effect! The loci are of such large effect I think that South Asian couples of middle complexion who want lighter skinned offspring can now feasibly engage in selective abortions to "load the die" so that their offspring are the "optimal" combination of their genes. We have the information and the technology. Then I began thinking, do people really care about total genome content in relation to their offspring? We've floated the possibility of switching a few hundred loci to shift the expected phenotypic value in the offspring, but the Murtaugh objection looms in the background. But we already have genetic backgrounds which have been "field tested" for viability and health in highly intelligent people. Why not just use them and fiddle around with the loci which control superficial physical appearance! What I'm saying here is that instead of taking the genetic material from one's own biological offspring and fiddling with hundreds of loci to shift the quantitative value of traits of interest such as height and IQ, why not create a clone of a tall and very intelligent person, and switch a few dozen loci so as to sculpt that individual so that it can pass as your natural offspring? Imagine that a Japanese couple hosts a tall Swedish exchange student who is both a stellar scholar and athlete, and is moderately tall to boot. Additionally, this individual has a very agreeable personality. The son they always wanted! Perhaps they can get that son. They could clone the student, and then make changes to complexion, hair form, eye color, nasal form and include in Asian traits such as the epicanthic fold. Eye color, hair color and skin color are known to some degree now, perhaps a dozen genes could do most of the trick. But what about nasal form? I don't honestly know. Epicanthic fold? Again, I don't know. I suspect that some of these traits are subject to QTLs of larger effect than height or intelligence. One would have to do the cost vs. benefit. Now, some of you might ask, "but why would people want to have offspring who are predominantly not descended from them?" Perhaps that is an issue for many or most people. Honestly though, I think if you could make a child resemble the midpoint of both parental phenotypes in terms of complexion and facial features the intellectual (conscious) knowledge would quickly be overruled by the reflexive (proximate) cognitive processes which would identify the physical resemblance and induce the normal emotional response (the main objection is that I do think that personality ticks are highly heritable, so perhaps some parents would start to treat their offspring as incongruous impostures who exhibit the right look, but with strange mannerisms). This goes to human psychology, it is a complicated area and there is some evidence that humans exhibit essentialisms which may transcend morphology. That being said, in this case I believe not all loci are created equal. If the "important" loci (those which contribute to visual parent-child resemblance) are identical by descent & state from the putative parents I think that many would enter into the tradeoff of alien genome content for the sake of building a "better baby." Anyway, just a thought I had on the way to the Post Office (I'm not shitting you!). Note: Even if the Murtaugh objection does not hold, it might be cheaper to do what I'm talking about. I don't really take the objection that much to heart, humans mix & match genes across genetic backgrounds all the time when we mate. The key would be to get the exogenous material in early during development so any problems would lead to a spontaneous abortion. Obviously playing with the genetic architecture after the child had been delivered might be more problematic. Also, though purchasing the rights to someone's genome for your offspring might be expense, I don't see how it would be that much more expensive than eggs purchased for fertility clinics are today. Of course, the types of parents I'm talking about are probably going to be in line for androids too. Let your imagination fly. Labels: Population genetics
Friday, October 19, 2007
 Some readers may recall something of a discussion on these pages between myself and Larry Moran regarding the relative importance of natural selection and drift in phenotypic evolution. My refrain was "it's an empirical question", so I'll point to two recent reviews that touch on the growing body of data that can be used to address the question. Some readers may recall something of a discussion on these pages between myself and Larry Moran regarding the relative importance of natural selection and drift in phenotypic evolution. My refrain was "it's an empirical question", so I'll point to two recent reviews that touch on the growing body of data that can be used to address the question. The first is titled, conveniently enough, "Which evolutionary processes influence natural genetic variation for phenotypic traits?". The authors, of course, can't really answer the question, but they point to a number of studies examining specific traits and how natural selection has influenced their evolution. The picture is from a striking example of adaptive variation in coat color in mice. Another example that particularly caught my eye was that of variation in flower color in Linanthus. Those of you familiar with classic population genetics will recall that Linanthus was one of Sewall Wright's preferred examples of neutral phenotypic variation driven by isolation [pdf]. He was, as it turns out, probably wrong. Molecular data has the power to answer a lot of these questions, or at least allow them to be posed in a more testable manner. The second review focuses on the species that is becoming/has become the modern "model organism" for studies of selection-- humans. It's a very thorough summary of the recent scans for selection in the human genome, and anyone looking to get up to speed on the topic should read it. Selection in pervasive in the genome, and perhaps the only way to understand how it acts is through statistical analysis of genome sequence. The authors make this explicit, with an interesting nod to the oft-cited Lewontin and Gould spandrels paper. There are those who argue that functional evidence is essential for defining a region of the genome as being under selection, however, the deductive logic between selection and phenotype only goes in one direction-- that is, a region identified as being under selection using statistical methods is necessarily functional (with a certain false positive rate), but, as a modern fan of the spandrels paper might write, evidence of function does not necessarily imply selection. Human evolution has become something of a trendy topic, but as is often the case, it's trendy for a reason-- there is extensive data on genotype, phenotype, and environment coming available on our species, and this will allow us to tackle some of the longest standing debates in evolutionary biology. They are, after all, empirical questions. Labels: Evolution, Genetics, Population genetics
Wednesday, October 17, 2007
In Genome-wide detection and characterization of positive selection in human populations there's an interesting part which intrigues me:
The EDAR polymorphism is notable because it is highly differentiated between the Asian and other continental populations...and also within Asian populations (in the top 1% of SNPs differentiated between the Japanese and Chinese HapMap samples). Genotyping of the EDAR polymorphism in the CEPH...global diversity panel...shows that it is at high but varying frequency throughout Asia and the Americas (for example, 100% in Pima Indians and in parts of China, and 73% in Japan)...Studying populations like the Japanese, in which the allele is still segregating, may provide clues to its biological significance. 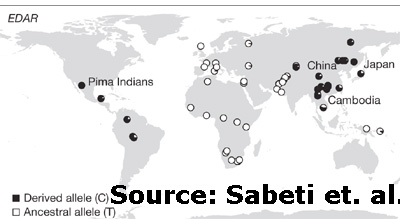 What's going on? My blind and fact-free guess is this polymorphism has something to do with hair form. Eye-balling the map I see that Cambodians are balanced for ancestral and derived, and they're the Southeast Asian population which is "Mongoloid" that stereotypically has the curliest hair. As for the ~73% value in Japan, that makes sense if you accept the finding that Japanese are hybrid population between Yayoi rice farmers from the East Asian mainland and Jomon natives to a ratio of 3:1, with the latter exhibiting the ancestral allele and the former the derived. The Jomon were probably a collection of people of whom the Ainu of Hokkaido are/were the last distinct remnants in the historical period. The Ainu of course have less stereotypically East Asian features despite their genetic relatedness to other groups in Northeast Asia. One of their characteristics is a tendency toward wavy hair. What's going on? My blind and fact-free guess is this polymorphism has something to do with hair form. Eye-balling the map I see that Cambodians are balanced for ancestral and derived, and they're the Southeast Asian population which is "Mongoloid" that stereotypically has the curliest hair. As for the ~73% value in Japan, that makes sense if you accept the finding that Japanese are hybrid population between Yayoi rice farmers from the East Asian mainland and Jomon natives to a ratio of 3:1, with the latter exhibiting the ancestral allele and the former the derived. The Jomon were probably a collection of people of whom the Ainu of Hokkaido are/were the last distinct remnants in the historical period. The Ainu of course have less stereotypically East Asian features despite their genetic relatedness to other groups in Northeast Asia. One of their characteristics is a tendency toward wavy hair.(note that this doesn't mean that I think there was selection for thick very straight hair. I assume it is likely a byproduct effect) Labels: Population genetics
The Samaritans: it's endogamy, not cousin-marriage (per se)
posted by
Razib @ 10/17/2007 01:14:00 PM
There's an article up about Samaritans. The community is small, down to 350, and traditionally endogamous. That's a problem:
To explain his decision, he points to his own family. When he was a young man, High Priest Elazar's father decreed that he should marry his cousin. It was a mistake, he says now. Two of his three sons were born deaf and mute. Two others died. Mr. Cohen is his only healthy child. But note, this isn't just because the Samaritans are marrying first cousins. Rather, generations of endogamy has cranked up the coefficient of relationship so that deleterious alleles are now extant at an extremely high frequency. In the United States first cousins who marry are generally related because two of the parents are siblings. The other two parents are unrelated. When considering the possibility of the appearance of a rare deleterious recessive disease you only need to focus on one side of your family tree, you're safe not putting too much effort into the unrelated portion because you assume that they carry different rare alleles. This isn't true for the Samaritans, they're closely related every which direction. In any case, inbreeding reduces the effective population size and so cranks up the ability of random genetic drift to fix deleterious alleles. Consanguinity among obligately endogamous societies is a different order of inbreeding than what you might know from in the West. Though cousin marriage is not unknown (e.g., Charles Darwin), but isn't scaffolded by amplifying social customs (i.e., inbreeding vs. inbreedinggeneration n). Also, note that one generation of outbreeding can mask the deleterious alleles immediately. Nevertheless, many subsequent generations will of course still be subject to the recessive diseases of the Samaritans (though at a lower frequency) because one assumes that people of substantial Samaritan ancestry will still assortatively mate. And so they will bring together the deleterious alleles again. H/T Ikram. Labels: Population genetics
Monday, October 01, 2007
Below is a graph of the derived allele frequency spectrum in the three HapMap populations (from here). Many papers have been written about this spectrum, statistics have been derived around it, arguments have gone on about its interpretation, and now...we can simply look at it. Data is a wonderful thing.
 ADDENDUM: I should probably give a little explanation of the graph. Razib has added the names to the population labels, and the dotted line gives the expected allele frequency spectrum (given their two-chromosome ascertainment strategy, in case you're wondering why it's a straight line and not theta/i) under the assumption of a constant population size. The shift towards rare alleles in the Yoruba indicates a population expansion in recent history, and the shift towards common variants indicates a population bottleneck (or a longer-term small population size) in the European and Asian populations. Labels: Population genetics
Saturday, September 22, 2007
In the middle of an otherwise boring New Yorker article about where to buy coats for the coming winter, I came across this passage, describing the author's (possibly tongue-in-cheek) search to understand why she seems to feel cold more acutely than other people:
I called Dr. Andrej Romanovsky... to ask how the body detects cold. According to Romanovsky, the going theory is that a newly discovered receptor (TRPM8, if you were wondering [I was!]) reacts to low temperatures. This same molecule also reacts to menthol, which accounts for the compound's cool feel on the skin. So why is it that certain people whine more than others when the temperature drops? "I don't think anybody studies what you want them to study, " Romanovsky told me.Not true, Dr. Romanovsky! Sometimes people study exactly what you want them to study. I googled my way to this study, entitled "Genetic predictors for acute experimental cold and heat pain sensitivity in humans": Background: The genetic contribution to pain sensitivity underlies a complex composite of parallel pain pathways, multiple mechanisms, and diverse inter-individual pain experiences and expectations.Ok, these associations are highly questionable (anyone want to fund a large genome-wide association study of cold tolerance to put the question to rest?), but still, there are scientists asking these sorts of questions. I also checked out a couple of the genes in Haplotter-- selection for cold tolerance was likely very strong as humans moved north out of Africa. There are some perplexing signals-- TRPM8 shows some evidence for selection, but in the Yoruba (Nigeria: probably not exerting a selection pressure for increased cold tolerance). TRPV1 (a receptor involved in heat tolerance) shows a huge signal in the Yoruba as well; this makes more sense. Nothing too exciting, I just was amused that my furious googling was inspired by an article about coats in the "style issue" of the New Yorker. And contrary to Dr. Romanovsky's claim, understanding why people feel cold differently is very much an active area of research (and well within the reach of current technology). Labels: Genetics, Population genetics
Wednesday, September 19, 2007
Nicholas Wade of the New York Times is, without a doubt, one of the best science reporters in America. Apart from his writing, which is of course excellent, he shows an impressively deep knowledge of his chosen subject (genetics)-- enough to write an excellent book on the topic and to effectively communicate subtle aspects of research (when he mentioned statistical power in a recent article, I may have choked up a little bit. It was really that beautiful).
So if you were, say, writing an article criticizing the coverage of genetics in the media, Wade should be absolutely the last person on the list of people to mention. However, a new article in Nature Reviews Genetics takes him to task for one of his uses of he word "race". Needless to say, I think it's absurd. From the article: An example of the constant slippage of race terms is provided by Nicholas Wade, who was a strong journalistic propagator of Neil Risch's claim that there are five major human races that are defined by genetic clusters, specifically, Africans, Caucasians, Asians, Pacific Islanders, and Native Americans. However, when reporting on recent diabetes research, Wade includes as his list of races, "African-Americans, Latinos, American Indians, and Asian-Americans." The social grouping we call Hispanics is not one of Risch et al.' s categories, and it does not share a stable, historically deep genetic cluster.First, perhaps I'm being overly sensitive about tone here, but on first reading this passage seemed to make Risch and Wade sound, I don't know...a little sinister. The "claim" being "propagated" by Wade is the simple fact that there is some clustering of genetic diversity according to broad geographic regions. Risch has long advocated (convincingly, in my opinion) that this genetic diversity not be ignored in medicine. Perhaps the public is interested in hearing about this research. Second, the list of "races" given by the author is a little silly. Risch has never made some kind of statement about which genetic clusters are "races" and which are not. In fact, I'm guessing the author of this paper hasn't read much of Risch's work. In a 2002 paper, he does indeed write, referring to a number of studies on the genetics of race: Effectively, these population genetic studies have recapitulated the classical definition of races based on continental ancestry - namely African, Caucasian (Europe and Middle East), Asian, Pacific Islander (for example, Australian, New Guinean and Melanesian), and Native American.But these clusters are not the only way to apportion genetic diversity, of course. Race is, to a certain extent, a social construct. How much genetic clustering do current social groupings (including the dreaded word "Hispanic") show? A good question, and luckily one Risch answered in a 2005 paper: Subjects identified themselves as belonging to one of four major racial/ethnic groups (white, African American, East Asian, and Hispanic) and were recruited from 15 different geographic locales within the United States and Taiwan. Genetic cluster analysis of the microsatellite markers produced four major clusters, which showed near-perfect correspondence with the four self-reported race/ethnicity categories. Of 3,636 subjects of varying race/ethnicity, only 5 (0.14%) showed genetic cluster membership different from their self-identified race/ethnicity.So if one is using the word "race" as defined by the options available when you check a box on a government form, races do indeed show some extent of genetic clustering. And for the record, here's the Wade quote that so exemplifies nefarious use of the word "race": While Type 2 diabetes is more common in African-Americans, Latinos, American Indians, and Asian-Americans, Dr. Stefansson said more studies were needed to see whether there were significant differences in the variant gene's distribution among races.Sounds pretty reasonable to me. Labels: Population genetics
Monday, September 17, 2007
Alex Palazzo gives a nice summary of a recent paper (open access) on adaptation in non-coding elements in mammals. The paper was mentioned briefly by Razib here.
Labels: Population genetics
On this site, there is often speculation about population differences in various phenotypes, and the role of genetics and natural selection in said differences. Hypotheses are lovely and all, but luckily there are publicly available resources that anyone can access and browse to determine whether their hypothesis has any empirical support. In this post, I provide a basic introduction to those resources. I note here that, given the rapid progression of knowledge in the area, this is likely to remain state-of-the-art for, oh, a couple months, tops.
I. Allele frequency resources  To start, let's say you have a hypothesis about the role of gene X in phenotype Y. If populations have different distributions of Y, you might also expect them to have different distributions of alleles of X, no? Seems reasonable. Unfortunately, there's no resource of population allele frequencies available (though one might expect this to change in the near future). The best things available now are the HapMap (which has genome-wide allele frequency information on four populations-- a western European population, the Yoruba from Nigeria, the Han Chinese, and a Japanese population from Tokyo) and ALFRED (a mishmash of allele frequency data compiled from various small studies). To see what these databases can do for us, let's take an example: perhaps you have heard of this trait called lactose tolerance, and a gene called lactase (LCT). The two SNPs (single nucleotide polymorphisms) that are putatively causal for lactose tolerance (ie. that allows one to digest lactose in adulthood) are located ~14000-20000 base pairs upstream from LCT, in an intron of a gene called MCM6. Let's check ALFRED to see if anyone has assembled allele frequency data on these SNPs. From the front page, I enter MCM6 in the quick search area (note I don't enter LCT, since the causal SNPs are actually in MCM6), and follow the link to the page for MCM6. The two SNPs I'm looking for are "intron 13 (C/T)" and "intron 9 (G/A)". If I click on, for example, the intron 9 SNP, I get to the entry for that SNP, where I can generate a map like the one on the right, or peruse the frequencies in table form. As seems reasonable, the T allele is common in Europeans and some Central Asian populations, but nearly absent elsewhere.  Of course, most SNPs aren't going to be in this database (I actually generally don't use ALFRED at all--any new SNP you're interested in isn't going to be in it), so let's do something similar with the HapMap. To do that, we note the intron 13 SNP is named rs4988235 (you can see this in ALFRED, but usually you won't need to--almost all SNPs are now referred to in all databases and papers by their rs number, which is standardized way of referring to SNPs). From the HapMap homepage, I click on the link to the genome browser (either one will do), and enter "SNP:rs4988235" in the "Landmark or Region" field. This brings me to the area, and one of the tracks of the browser gives the allele frequencies, as seen on the right. Again, Europeans (labeled CEU) have high frequency of the causal allele, which is absent elsewhere. II. Selection resources  So alleles controlling the expression of LCT show population frequencies in line with explaining the differences in the distribution of lactose tolerance worldwide (to a rough extent). Now, could those alleles be under natural selection? To test this, we turn to Haplotter, a database of summary statistics designed to test for recent positive selection. The underlying data is from the HapMap, so only three populations are available (here, the Chinese and Japanese are condensed into a single Asian population). The summary statistics calculated are iHS, D, H, and FST. I don't intend to give a full exposition of what each of these statistics is, but briefly, iHS is a summary statistic of the haplotype structure surrouning a region, which has power to detect selective sweeps that are incomplete, D and H are summary statistics of the frequency spectrum that have power to detect sweeps that are complete/nearly complete, and FST is a measure of allele frequency differentiation between populations. So let's take a look at LCT (in this case, since the statistics are calculated on a region, we could look either at LCT or MCM6). From the Haplotter home, I enter "LCT" in the "Query by gene" area, which brings up a number of plots. The relevant statistic here is iHS, as the alleles we're interested in are still polymorphic (see the figures above). On the right, you see the iHS plot for the region. Clearly, the European population (the blue line) has extraordinarily elevated values, and the Yoruban and Asian composite populations do not. This could be interpreted/has been interpreted to demonstrate a very strong selection on the ability to digest lactose in our recent history. Like I said, these resources will likely be obsolete soon, but for now they're fun places to browse and test various hypotheses with. So take your favorite gene, look for selection on it in Haplotter, check the allele frequency differences in the HapMap, and hey, don't be afraid to tell us what you find. Addendum from Razib: The comment thread below is also going to be an "open thread." You can see it to the top right in the sidebar as Find any genes?. If you think you've found something interesting through these resources, post it there! There are only a finite number of eyes looking at these heaps of data (or brains writing lines of code to analyze them), so there's no downside in adding some more.... Labels: Genetics, Population genetics
Wednesday, September 05, 2007
Almost a year ago, Svante Paabo's group published an article reporting a million base pairs of DNA isolated, in principle, from Neandertal bone. The results were striking, in that Neandertals appeared much closer, genetically, to humans than one might expect. Well, Nature News has an article this week about a paper in PLoS Genetics arguing that the reason for this could actually be quite parsimonious: contamination from modern humans. From the news report:
Svante Paabo, senior author of the Nature paper, concedes that his group at the Max Planck Institute for Evolutionary Anthropology in Leipzig, Germany, had problems with contamination. These prompted him to change laboratory procedures and to add controls late in 2006, after the paper was published. "I agree with [Wall's] analysis," Paabo says. "Their observations are formally correct."The paper estimates the amount of contamination at about 80%, which is pretty atrocious. The irony here, of course, is that Paabo was one of the people who made sequencing ancient DNA feasible again after fiascoes like reports of "dinosaur DNA"-- the "dinosaur" sequences ended up matching up pretty well with some of the lab members, and it appears Paabo has made the same mistake here. Fortunately, this is likely only to be a minor setback--the other group working on the DNA seems to have avoided the contamination problems, and presumably Paabo's most recent work will be more careful about it. Labels: Neandertals, Population genetics
Wednesday, August 22, 2007
Baltic neighbours face alcohol crisis:
The Estonian government plans to raise taxes on alcohol by 30% next year as the small Baltic nation of 1.3 million is struggling with a drink problem.... In related news, Evidence of positive selection on a class I ADH locus:
What's going on here? As a great man once said, maybe it's agriculture? Though seriously, I doubt that protection against alcoholism here is a major issue. So why is it being selected? Who knows. It seems likely that ADH1B is somehow involved in metabolization of various biochemicals which might have fitness implications. What are these populations consuming? And what aren't the other populations consuming? Or, perhaps they're consuming similar things (at least biochemically), but other (e.g., Near Eastern) populations have different selected alleles or functionally relevant loci which result in no great selection on the ADH1B allele in question. Labels: Behavior Genetics, Population genetics
Tuesday, August 21, 2007
 There's a nice review in the most recent Trends in Genetics on the use of spatially explicit models in human population genetics. As everyone knows, classic population genetic theory generally makes very restrictive assumptions about the amount of structure in a population-- that is, that there is none. Or maybe a couple populations that exchange migrants. These are all nice assumptions for making the math less hairy, but the recent influx of data (largely generated for medical genetic purposes) on populations from around the globe has revived an interest in modeling variation in a more flexible manner. Along with every person comes their approximate latitude and longitude-- how does genetic data vary on those axes? There's a nice review in the most recent Trends in Genetics on the use of spatially explicit models in human population genetics. As everyone knows, classic population genetic theory generally makes very restrictive assumptions about the amount of structure in a population-- that is, that there is none. Or maybe a couple populations that exchange migrants. These are all nice assumptions for making the math less hairy, but the recent influx of data (largely generated for medical genetic purposes) on populations from around the globe has revived an interest in modeling variation in a more flexible manner. Along with every person comes their approximate latitude and longitude-- how does genetic data vary on those axes? The review is a nice summary of recent work in the area, which has shown that a progressive two-dimensional stepping stone model is, for the moment, a decent approximation for human variation (the bottom part of the figure shows parts of the world shaded according to heterozygosity. The largest values are in Africa, where humans originated, and gradually go down, through the serial bottleneck, the further you go from the origin). But this field is ripe for new models and theory. And exploring new models, of course, leads to overturning old ones. Labels: Genetics, Population genetics
Thursday, August 09, 2007
Neat article on the introgression of an allele for switching the red seeds of rice to white from the japonica to the indica subspecies. Basically the mutant arose in the japonica subspecies, "jumped" to the indica, and fixed. You can read the paper for why people prefer white to red varieties, but the important point that the authors offer is that a) rice is highly inbred and b) there are fertility barriers between the two varieties. That implies that the selective advantage was so great that people worked hard to hybridize the two even though it was something of an unnatural act.
Labels: Population genetics
At my other blog I have a long post reviewing the new paper on lactase persistence in Eurasia. The authors conclude that the allele which confers most of the latcase persistence in Eurasia arose among "Caucasian" populations. The question is whether the authors meant Caucasian in the 1930s physical anthropological sense (i.e., Caucasoid-Mongoloid-Negroid), or in the more precise sense of peoples from the Caucasus. Here is the portion of the paper which might "clear" this up:
We also monitored the prevalence pattern of the less common LNP [lactase non-persistence -ed.] H87 haplotype that, on the basis of the MJ network, represents the immediate allelic haplotype on which the LP H98 mutation occurred. The highest frequencies of H87 alleles were observed among Daghestan Nogais (8%) and Hazara (7%). This allele was detected in Daghestan Nogais, Hazara, Baluch, Sindi, Brahui, Makrani Baluch, Iranians, Basques, individuals from Utah, and Finns (eastern region). From this distribution of H87, we were able to propose that the ancestral population in which the LP T-13910 H98 mutation occurred is of Caucasian origin. The Daghestani Nogais are a Turkic group in the Caucasus. None of the rest are technically Caucasian groups. Here are the populations that exhibit H87 with the percentages and N's:
The N's aren't as big as you'd like (I know, this is like saying "I'm not as rich as I wish I were!"). H87 is a haplotype one mutational set away from H98, the modal variant associated with lactase persistence throughout Eurasia. The haplotype two mutational steps away from H98 (see the chart on my other blog), H84, has high frequencies throughout Eurasia, but its center of gravity is shifted toward the east (i.e., France has a far lower proportion than China). I think that this implies that H98 and the dominant LP genetic profile arose somewhere in the heart of Eurasia, probably the north-central regions. Now, one thing that I am curious about are the non-modal alleles, some of which seem to be independent mutational events from a different genetic background than H84/H87. As noted before these variants are: 1) Very new (on the order of 2,000 instead of 8,000 years ago for the most recent common ancestor). 2) Rather rare. Here are the percentages in the populations which exhibit the haplotypes associated with the more recent mutational event. I've also included to the right the percentage in the older cluster, and finally the N's:
What to say here? First, the highest frequencies are found in populations along the Urals. Iranians also seem to have high frequencies of the newer alleles. I am curious about the relative balance between the older and newer alleles in several of the higher frequency populations. If the older variant exists why would the newer one rise in frequency over the past few thousand years? If the older variant exists why did it not sweep to fixation? If the selection pressure was too weak (or various balancing forces maintained polymorphism) to fix the older variant why did the newer mutational event begin to rise in frequency in the first place? Here are some thoughts: 1) LP is weird. It has to come with some cost, probably metabolic. With the domestication of cattle any costs were overridden by the benefits of adult milk consumption. Perhaps the new mutational event has associated functional elements around T-13910 which make them a better solution? Perhaps there are regulatory elements which mask some of the negative correlated responses due to this mutation? 2) The populations which have the highest proportion of LP (northwest Europe) don't seem to exhibit the new variants. What gives? The selection pressure is obviously strong for anything that confers LP. We know that some African and Middle Eastern populations have other LP conferring SNPs besides T-13910, but the major groups above already had that, and, they were likely to be near the source of the rise of frequency of the mutant in the first place (judging by the distribution of H84/H87). Perhaps there is selection pressure for LP around the Urals (extant diary culture), but there are other forces which prevent its increase (maintain polymorphism). So the new mutant and associated haplotype might be a response to (counter) pressure #2. Pressure #2 might not be operative in western Eurasia so it is just another neutral allele because it doesn't have any fitness boost. 3) It seems suspicious to me that it seems likely that both clusters arose in central Eurasia. It isn't like there are more cosmic rays or enormous populations churning out mutations here. My own suspicion would have been that central Eurasia would just have a diversity of descendants from the original mutant from H87, but that doesn't seem like what's going on. A de novo mutational event occurred. Don't know what to make of that. There's other things lurking the background. Labels: Population genetics
Wednesday, August 01, 2007
Recent Genetic Selection in the Ancestral Admixture of Puerto Ricans:
Recent studies have used dense markers to examine the human genome in ancestrally homogeneous populations for hallmarks of selection. No genomewide studies have focused on recently admixed groups-populations that have experienced admixing among continentally divided ancestral populations within the past 200-500 years. New World admixed populations are unique in that they represent the sudden confluence of geographically diverged genomes with novel environmental challenges. Here, we present a novel approach for studying selection by examining the genomewide distribution of ancestry in the genetically admixed Puerto Ricans. We find strong statistical evidence of recent selection in three chromosomal regions, including the human leukocyte antigen region on chromosome 6p, chromosome 8q, and chromosome 11q. Two of these regions harbor genes for olfactory receptors. Interestingly, all three regions exhibit deficiencies in the European-ancestry proportion. The settlement of the New World in the Iberian colonies is characterized by two broad dynamics. First, the mass die offs of many populations due to the introduction of Eurasian pathogens. Second, the hybridization of indigenous female lineages with European male ones (and later African ones). Until recently it was assumed that the Puerto Rican population was dihybrid, that is, Africans and Europeans. But new data suggests a substantial indigenous maternal contribution. Labels: Population genetics
Sunday, July 29, 2007
Razib recently mentioned a paper on a polymorphism regulating memory in Drosophila. As I often do when studies like these are published, I determined the human homologue of the gene in question (PRKG1, in this case), and checked out the plots of summary statistics available online. Sure enough, there are peaks in the significance of iHS, Tajima's D, and Fay and Wu's H in the area (all signs of recent selection), though strikingly these peaks are only evident in the Asian population. Hm.
Labels: Population genetics
Wednesday, July 18, 2007
New Pritchard paper, Adaptive evolution of conserved non-coding elements in mammals
posted by
Razib @ 7/18/2007 10:10:00 AM
Jonathan Pritchard has a new provisional paper, Adaptive evolution of conserved non-coding elements in mammals, in PLOS Genetics:
Conserved non-coding elements (CNCs) are an abundant feature of vertebrate genomes. Some CNCs have been shown to act as cis-regulatory modules but the function of most CNCs remains unclear. To study the evolution of CNCs we have developed a statistical method called the 'shared rates test' (SRT) to identify CNCs that show significant variation in substitution rates across branches of a phylogenetic tree. We report an application of this method to alignments of 98,910 CNCs from the human, chimpanzee, dog, mouse and rat genomes. We find that 68% of CNCs evolve according to a null model where, for each CNC, a single parameter models the level of constraint acting throughout the phylogeny linking these five species. The remaining 32% of CNCs show departures from the basic model including speed-ups and slow-downs on particular branches and occasionally multiple rate-changes on different branches. We find that a subset of the significant CNCs have evolved significantly faster than the local neutral rate on a particular branch, providing strong evidence for adaptive evolution in these CNCs. The distribution of these signals on the phylogeny suggests that adaptive evolution of CNCs occurs in occasional short bursts of evolution. Our analyses suggest a large set of promising targets for future functional studies of adaptation. Interestingly, there another paper another paper out in PNAS which speaks to the possibility of non-coding genomic regions in humans having functional significance. Labels: Population genetics
Tuesday, July 03, 2007
Larry Moran has a response to my post on adaptation. I say my piece in the comments on that post, and RPM has some further thoughts:
The modern selectionist does not invoke adatationist explanations for every evolutionary change. But he does not, by default, say "drift did it", either. Instead, he requires evidence for whichever conclusion he reaches. Maybe he's not really a selectionist; maybe he's just a population geneticist who understands how to detect selection.This is the beauty of these here internets-- every time you start talking out your ass, there are enough people watching that most of the time someone will call you on it[1]. If I ever make a bone-headed remark about biochemistry, I certainly hope Larry Moran shows up and corrects me in the comments. [1] I should be clear-- I'm not being facetious at all. Labels: Evolution, Population genetics
Friday, June 29, 2007
The Genographic Project Public Participation Mitochondrial DNA Database. This is Spencer Wells' baby. Only mtDNA, and focused more on the methods though they didn't find Neandertal lineages.
Labels: Population genetics
Wednesday, June 06, 2007
Results from the most ambitious (and expensive) set of genome-wide association studies for common diseases were published today in Nature (open access! You can read it for free!). Funded by the Welcome Trust in the UK, a "dream team" of clinical geneticists and statisticians assembled a common set of 3000 controls to compare genetically to around 2000 cases each of Type I diabetes, Type II diabetes, arthritis, cardiovascular disease, Crohn's disease, bipolar disorder, and hypertension.
This study is being trumpeted as a major success, and to some extent, it is-- for all diseases except hypertension, at least one strong signal and many weaker signals were identified. As correlational studies are largely hypothesis-generating, some of these will lead to major discoveries about the pathology of disease. In Crohn's disease, for example, the consortium has found a couple loci involved in autophagy and the elimination of intracellular bacteria. They also confirm the association of another locus involved in autophagy. It's easier for people working on a disease to focus on pathways that are already known to be involved in the disease (for example, there's a known autoimmune component to Crohn's disease); it often takes this kind of top-down study to jolt people out of complacency. The consortium has also make publicly available an impressive suite of software, along with new algorithms for genotype calling and mutlti-locus association, incorporating information from the HapMap. These tools are certainly at the cutting edge, and represent major advances in their own right. On the other hand, one can't help but notice that the loci identify contribute only a fraction of the known genetic component of these diseases. This is a proof of principle-- the base has been laid; it's now feasable to scale these sorts of case-control studies up to tens of thousands of individuals. But is that really the most effective way at getting at the genetic basis of these diseases? Perhaps not. A final comment-- I noted in the comments of a previous post that the big data sets used for population genetics these days are generated for medical reasons. There's a ton of population genetic information here, which the authors are likely going to make more use of the future. They do give us a glimpse, though-- they note a number of genomic regions that show marked geographic variability within the UK (and note they limit themselves to self-identified "white Europeans"): Thirteen genomic regions showing strong geographical variation are listed in Table 1, and Supplementary Fig. 7 shows the way in which their allele frequencies vary geographically. The predominant pattern is variation along a NW/SE axis. The most likely cause for these marked geographical differences is natural selection, most plausibly in populations ancestral to those now in the UK. Variation due to selection has previously been implicated at LCT (lactase) and major histocompatibility complex (MHC), and within-UK differentiation at 4p14 has been found independently, but others seem to be new findings. All but three of the regions contain known genes. Aside from evolutionary interest, genes showing evidence of natural selection are particularly interesting for the biology of traits such as infectious diseases; possible targets for selection include NADSYN1 (NAD synthetase 1) at 11q13, which could have a role in prevention of pellagra, as well as TLR1 (toll-like receptor 1) at 4p14, for which a role in the biology of tuberculosis and leprosy has been suggested. Labels: Association, Genetics, Population genetics
Thursday, May 10, 2007
Reading an agressively-stated scientific opinion is an acquired taste-- in published work, academics prefer to subtly hint that their colleague is ass, rather than just saying it directly like we do here on the internets. But when one is used to the dry writing of the scientific research articles, those subtle (or sometimes not so subtle) digs come to be rather enjoyable.
Which is why I enjoyed this piece by Michael Lynch [pdf], just published in PNAS. Dr. Lynch has long been an advocate for taking population genetics forces into account when studying genome evolution and innovation, and here he makes his case: Although the basic theoretical foundation for understanding the mechanisms of evolution, the field of population genetics, has long been in place, the central significance of this framework is still occasionally questioned, as exemplified in this quote from Carroll (4), "Since the Modern Synthesis, most expositions of the evolutionary process have focused on microevolutionary mechanisms. Millions of biology students have been taught the view (from population genetics) that 'evolution is change in gene frequencies.' Isn't that an inspiring theme? This view forces the explanation toward mathematics and abstract descriptions of genes, and away from butterflies and zebras. . . The evolution of form is the main drama of life's story, both as found in the fossil record and in the diversity of living species. So, let's teach that story. Instead of 'change in gene frequencies,' let's try 'evolution of form is change in development'." Even ignoring the fact that most species are unicellular and differentiated mainly by metabolic features, this statement illustrates two fundamental misunderstandings. Evolutionary biology is not a story-telling exercise, and the goal of population genetics is not to be inspiring, but to be explanatory.His argument is that many of the features of the eukaryotic cell, often assumed to be products of adaptations, may be largely the result of deleterious fixations due to a much smaller eukaryotic effective population size. It remains unclear how these features-- introns, large genomes, some aspects of gene regulation-- came to arise given their apparent costs. According to Lynch, population genetics provides a simple framework for testing neutral versus adaptive hypothesis on this subject (he favors neutral explanations). This has been largely ignored due to, well, the fact that math is hard: The field of population genetics is technically demanding, and it is well known that most biologists abhor all things mathematical. However, the details do matter in the field of evolutionary biology.Overall, he presents a sort of neutral theory of genome evolution, or at least the beginnings of one. And I must admit I'm intrigued by this possibility that "a long-term synergism may exist between nonadaptive evolution at the DNA level and adaptive evolution on the phenotypic level". Some possibile examples of this: one of the current roles of the nuclear membrane is to segregate the actions of transcription from those of translation so that introns can be spliced out before a protein is made. It's an interesting hypothesis, then, that the nuclear membrane itself (one of the defining hallmarks of a eukaryotic cell) evolved in response to the existence of introns. Lynch cites another paper arguing that the nonsense-mediated decay pathway could also have evolved to prevent the translation of transcripts resulting from splicing errors. Finally, I've also heard much speculation that many of the regulatory mechanisms we take for granted-- methylation, histone modifications, etc.-- could have evolved to silence selfish DNA elements before taking on the broader roles they play today. Sewall Wright put much emphasis on the role of genetic drift in allowing the evolutionary process to cross regions of low fitess to find other adaptive peaks. Maybe early population geneticists really did discover everything worth knowing about evolution. Labels: Evolution, Population genetics
Monday, May 07, 2007
A recent paper on the relative number of genes that have undergone positive selection in chimps and humans recieved quite a bit of press (see Razib's comments here, here, and here). The title is quite provocative ("More genes underwent positive selection in chimpanzee evolution than in human evolution"), so I finally gave it a read. Frankly, if you haven't read it already, don't waste your time.
Let's grant the authors their starting position-- that there is a "common belief" that more genes have undergone positive selection in the human lineage than in the chimpanzee lineage (I would argue that this belief isn't all that widespead, though ultimately the reasons for the intiation of the study are irrelevant). In theory, addressing the veracity of this claim is easy-- make a list of the genes that have undergone positive selection along the human lineage, make a list of the genes that have undergone positive selection along the chimp lineage, and start counting. The devil, of course, is in the details. Due to the fact that not every selected gene will leave a detectable signature, the major assumption of the authors' analysis, then, is that the fraction of detected selected genes along the human lineage is the same as the fraction of detected selected genes along the chimp lineage. That is, if the number of genes that have undergone positive selection in both lineages is the same, but 75% are detected in chimps and only 50% are detected in humans, one might erroneously conclude that more genes have undergone selection in chimps than in humans, while in truth the number of selected genes is the same. This, I will argue, is precisely the mistake made in this paper. Let's take a look at how the authors identified genes that have undergone positive selection. The basis of the test is essentially the ratio of non-synonymous to synonymous changes in a given gene along a given lineage (non-synonymous changes alter the amino acid sequence of a protein and are presumed to be functional, while synonymous changes do not changes the sequence of a protein and provide a sort of background substitution rate). So if there is an excess of non-synonymous changes (a ratio > 1), one might conclude that the gene has been subject to positive selection. The power of this test to dectect selection is contingent on finding an excess of amino acid-changing substitutions in a lineage. So what could alter said power? First, it's clear that a single selected site will alter the ratio only slightly, two selected sites will alter it a little more, three even more, etc. So the more selective fixations that occur in a gene, the more power the test will have to conclude for selection. On the other hand, take the number of synonymous substitutions-- if there are more of these, the levels of "noise" are elevated relative the levels of "signal", and there is lower power to conclude for selection. There is a major difference between historical human and chimpanzee populations that alters the power of the test in the two lineages; indeed, the authors mention this difference without really grasping why it discounts their conclusions. That difference is population size. Humans have historically had a smaller effective population size than chimpanzees and, as the authors note, natural selection is more efficient in a larger population. Thus, advantageous alleles can be pushed to fixation with greater probability, while neutral or deleterious alleles are fixed at a lower rate. So smaller populations should have overall higher levels of substitution (assuming positively selected changes are a minority of all fixations). This is exactly what is seen in the data-- humans have 30,083 synonymous fixations and 19,000 non-synonymous fixations, while the numbers for chimp are 29,644 and 17,701, respectively. These changes in the rates of allele fixations should lead to a weaker signal of selection in humans, and thus less power to detect it. It's no surprise, then, that the authors find less selected genes in humans than in chimps. Even if the number of selected genes were exactly the same, the relatively stronger signal of selection in chimps should produce exactly the same result. Perhaps the authors want to argue that fewer amino acid changes have been fixed by positive selection in humans than in chimps; this is what population genetics theory predicts, and may be true. However, to extrapolate from a number of amino acid changes to a number of genes is problematic; a single adaptive change in a gene could have major phenotypic consequences without being detected with the sorts of tests employed in this study. Labels: Evolution, Genetics, Population genetics
Tuesday, April 24, 2007
When we talk about genetic variation between populations, most of the time we're referring to SNPs or other "simple" polymorphisms, mostly because that's what we have data on. Detailed population genetics studies of copy number variants are just starting to appear; this paper is one of them. It's an anlysis of the frequency of a deletion of the gene APOBEC3B, involved in immunity to retroviral infection. As you can see in the map below, the gene is present in most people of European and African descent, but is missing in a significant fraction of Asian and Native American populations. Nothing revolutionary here, but expect more studies of this sort in the future.
ADDENDUM: I hasten to add, lest RPM read this post, that when I say these studies are starting to appear, I'm speaking about these sorts of studies in humans. In Drosophila, large deletions and inversions are the classic genetic polymorphisms used in population genetic analyses (due to their easy visibility in polytene chromosomes).  Labels: Population genetics
Thursday, September 21, 2006
 Identifying genes underlying skin pigmentation differences among human populations:
There are many posts about skin color in the GNXP archives. This should not surprise. The fact that SLC24A5 was positively selected for in Europeans and correlates with light skin, but remains ancestral in both Africans and East Asians, while the Arg163Gln variant of MC1R seems under selection in East Asians, but under relaxed selection or possibly diversifying selection in Europeans suggests that different genetic strategies are scaling the same phenotypic fitness landscape. Additionally, two different strategies suggests to me that gene flow has been low enough so that one best case strategy (i.e., the highest fitness peak in a large admixing population) isn't automatically selected across Eurasia across the common genetic background. You know what they say, selection is stochastic.... Labels: Pigmentation, Population genetics |



