Walker's World: French births soar:

The second development to note is that INED, France's National Institute of Demographic Studies, has done some detailed research and concluded that France's immigrant population is responsible for only 5 percent of the rise in the birthrate and that France's population would be rising anyway even without the immigrant population.
...
In fact in France, like everywhere else in Europe, the birthrate among immigrant mothers drops quickly toward the local norm in less than two generations. The measure most commonly used in international statistics is the Total Fertility Rate, which seeks to measure the number of children born to the average woman in her fertile years...

In France, the TFR has risen from 1.66 in 1993 to 2.0 in 2003 and 2.1 last year. If maintained, that means the population of France will rise from 60.7 million today to 70 million sometime before 2050.
...
The birthrates of Muslim women in Europe have been falling significantly for some time. In the Netherlands, for example, the TFR among Dutch-born women rose between 1990 and 2005 from 1.6 to 1.7. In the same period for Moroccan-born women in Holland it fell from 4.9 to 2.9, and for Turkish-born women in Holland from 3.2 to 1.9.

In Austria, the TFR of Muslim women fell from 3.1 to 2.3 from 1981 to 2001. In 1970 Turkish-born women in Germany had on average two children more than German-born women. By 1996 the difference had fallen to one child and has now dropped to 0.5....

A few points. First, even if there is convergence differentials still do matter. One thing I noted when surveying data on Mormon fertility is that though it has converged with non-Mormon fertility, the "floor" still usually remains higher than that of local non-Mormons. I'm not worried about a Mormon future of course because it is also a religion with a relatively high defection rate, but long term persistence of small differences do matter. Second, projecting to the year 2100 as many do today is very problematic. In the late 19th century some bureaucrats in the Ottoman government were relieved as the Christian Balkan provinces fell away through independence or assimilation into the Austro-Hungarian monarchy. The reason being the fact that Christians had higher fertility than Muslims; something most Muslims and Christians today would find a very peculiar worry. In After Tamerlane there is a reference to a racial triumphalist demographer writing in 1900 about the "fact" that in the year 2000 there will be 1.5 billion whites and only 400 million Han Chinese. Finally, variance matters. Note:

Germany is something of an oddity in this. In most countries with low fertility, young women have their first child late, and stop at one. In Germany, women with children often have two or three. But many have none at all.

Italy and Germany might both have low expectations in regards to the number of children a woman may have in her lifetime, but the shape of the distribution may matter a great deal if fertility is heritable to any extent (straight out of Genetical Theory here). Heritability need not be physiological; rather, it might be cultural and psychological propensities transmitted to the next generation. But if the data above hold one might expect German fertility to bounce back faster than Italian because a subset of the German population exhibit pro-natalist sentiments.

(H/T Talk Islam)

Labels: Demographics, fertility

This week, Probability.

John Hawks, in a post on scientists who dispute the acceleration hypothesis (acceleration deniers?), makes reference to "the Stanford school of genetic orthodoxy". So what is this?

Essentially, he's referring to the current paradigm (I'm as much of a fan of hyperbole as anyone else, but paradigm is clearly the more appropriate word here) in the field of population genetics about the peopling of the world. The story goes like this: a small set of individuals from an ancestral population in Africa moved somewhere in the Middle East, and grew. Then from there, a small set of individuals moved nearby in each direction and settled. Ditto for those populations, and so on. These "serial bottlenecks" kept occurring until the entire world was populated, replacing the individuals that were there before them.

The observation that solidified this paradigm comes from this paper, which showed an impressive negative correlation between distance from East Africa and genetic diversity, consistent with each population containing a subset of the diversity of the populations it came from. Since then, that sort of approach has been used in a number of similar applications, including this nice one on the peopling of the Americas.

Further support for this paradigm comes from more recent work modeling human demography--it's simply not true that this out-of-Africa hypothesis is enforced like an orthodoxy. See, for example this paper entitled "Statistical evaluation of alternative models of human evolution" (lest you think that alternative models of human evolution aren't being evaluated), which concludes for a single origin of humans in Africa. This doesn't test the "serial bottleneck" model, but does address the multiregional hypothesis, which I think is the major point for Hawks. Or consider a more recent paper, which attempts (with moderate success) to infer the colonization history of the world. The results favor out-of-Africa, as well as serial bottlenecks (though theses bottleneck, it must be noted, were essentially built into their model).

Now, new data may alter some of these models somewhat--David Reich and other claim here (in a News and Views article) that they see evidence for multiple waves of migration from Africa in PCA analysis, though it remains to be seen how those results hold up.

I'm not sure what Hawks thinks of these papers--for all I know, they're making the multiregional hypothesis into a statistical straw man that is easily demolished, but the point remains that the consolidation of these observations into a paradigm is not entirely without reason. The statistical methods and genetic data are available to challenge it, and skeptics (I know many) are more than welcome to try their hand.

Labels: Population genetics

Innovation in genetic variation research garners Jonathan Pritchard HHMI investigator appointment at University. HHMI = Howard Hughes Medical Institute. So when are we going to see him in Chicago Magazine? In any case:

In a 2006 paper, Pritchard and his colleagues described the identification of several hundred DNA regions in various human populations that show signals of selection. Included within those regions are genes that influence reproduction, olfaction and degradation of environmental toxins, skin pigmentation and skeletal development.

Using more extensive data that have recently become available, his group has been examining the relative roles of chance (which can lead to changes in the gene pool known as genetic drift) and selection in favoring these genes. "Selection may be a weaker force than we thought," he said. "It seems to be a combination of drift and selection acting together."

Things that make you go hmmmmm....

Positive Selection in East Asians for an EDAR Allele that Enhances NF-κB Activation:

Genome-wide scans for positive selection in humans provide a promising approach to establish links between genetic variants and adaptive phenotypes. From this approach, lists of hundreds of candidate genomic regions for positive selection have been assembled. These candidate regions are expected to contain variants that contribute to adaptive phenotypes, but few of these regions have been associated with phenotypic effects. Here we present evidence that a derived nonsynonymous substitution (370A) in EDAR, a gene involved in ectodermal development, was driven to high frequency in East Asia by positive selection prior to 10,000 years ago. With an in vitro transfection assay, we demonstrate that 370A enhances NF-κB activity. Our results suggest that 370A is a positively selected functional genetic variant that underlies an adaptive human phenotype.

We've blogged about EDAR before; Could it be hair form?, EDAR controls hair thickness and EDAR and hair thickness. The story here is simple, before the populations ancestral to the Native Americans had left eastern Asia a mutation on the EDAR gene swept nearly to fixation among these populations. The derived SNP in particular is correlated with the thicker hair typical of East Asians and Native Americans. In other populations (Europeans, Africans, West and South Asians as well as Papuans and Melanesians) the SNP is in an ancestral state. The main twist in this study is that they used a molecular genetic technique to show that this derived state seems to upregulate the activity of NF-κB transcription factor.


For the record, I'm really skeptical that this selective sweep occurred because the human populations of late Ice Age eastern Asia developed a really strong attraction to thick luxuriant hair with full body. The paper is Open Access, read the whole thing. Since the most interesting figure is either too small or too large, I've resized it appropriately and placed it below the fold.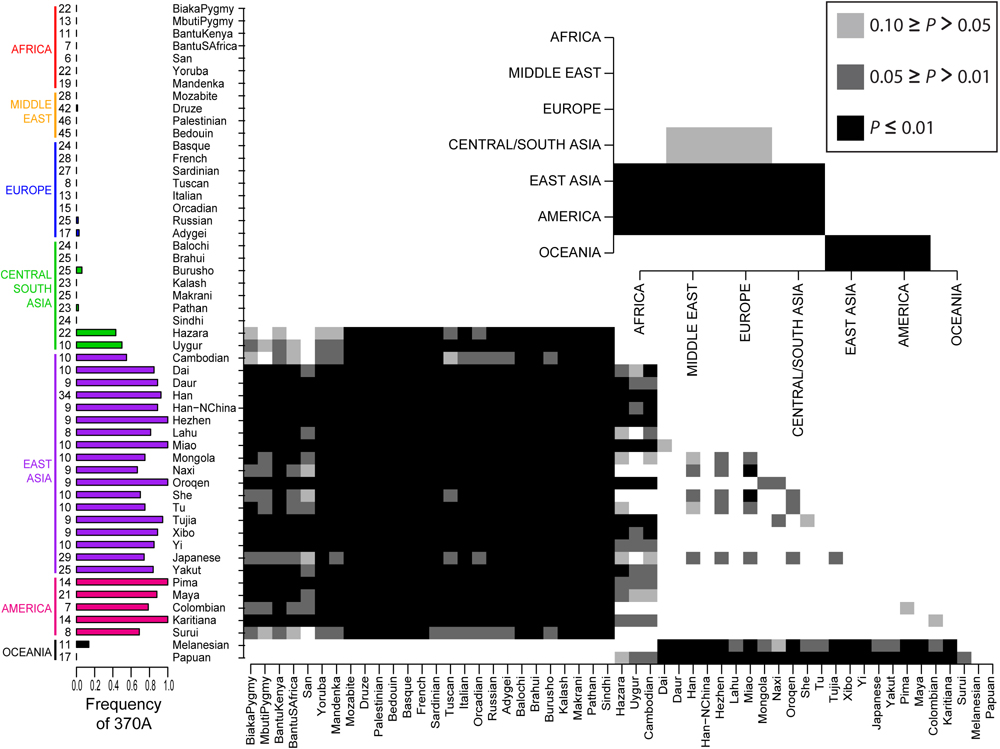

Labels: Population genetics

The debate over at The American Scene on Jim Manzi's article "Undetermined" is now closed to comments so I couldn't respond to one of the comments but the beauty of being a blogger is that you can use your own forum to vent your response.

The comment that I desperately wanted to respond to was left by Joe Shipman and reads as follows:

One thing that is established beyond any possibility of scientific doubt, of course, is that the genetic variability in IQ within races is much larger than the variability between races; any ethnic group of nontrivial size will have plenty of smart people and plenty of dumb people, and basing, say, educational policy on group rather than individual characteristics is therefore not only unAmerican but scientifically misguided.

Joe, will you join with me in advocating the complete dismantling of efforts to ameliorate the racial and gender wage gaps that exist, in that they too demonstrate that wage variability is larger within groups than between groups? I hit on this topic a few years ago:

It is important to recognize that most wage inequality occurs within and not between groups. The unweighted average Gini coefficient across all race, gender, and education groups was 0.256 in 1995, over 80 percent of the total Gini. Put another way, if all groups had identical mean wage rates (for example, black male dropouts had the same average wages as white male college graduates) but wages differed within groups as they do today, nearly all the inequality in wage rates would remain.

You know, if it's unAmerican and unscientific to craft social policy on observed group differences then surely the fact that the variability in Black or Hispanic incomes is greater within their groups than it is between their group and, say, Caucasians or Asians, is an unscientific and unAmerican basis upon which to craft social policy to address the between group differences in income. What's good for the goose is good for the gander, right Joe?

Labels: human biodiversity

Via Reihan, Instapaper. Need to not get behind on my Tech Crunch feed....

(any other "life hacks" you know of?)

Segment 3 on PRI's To the Best of our Knowledge.

A few weeks ago Steve mentioned Raymond Crotty's When Histories Collide: The Development and Impact of Individualistic Capitalism. When I clicked through the link the cover looked familiar; turns out that I'd seen it at my local used book store and had passed on it since I already had a backlog of economic history I was working through. But Steve's post piqued my interest, and Greg also had mentioned Crotty's lactose tolerant-centric theory of history. So I purchased it, and read it over the past week. Even including the foreword and preface this is a short work, around 300 pages, but When Histories Collide is relatively data dense and at times almost inscrutable to anyone not stepped in Irish agricultural economics & cliometrics. The text has a disjointed feel, and Crotty's son who had to edit the work after his father's death notes that he placed the Irish chapters near the end of the narrative despite the fact that they would likely have been interspersed through the text seamlessly if his father had his way. Though the author's death before the final revisions to When Histories Collide might have dampened its public reception somewhat, I have to observe that Crotty's swan song is laced with far more quantitative econometric detail than Greg Clark's Farewell to Alms. Combined with the constant algebra of factors of production and implicit references to comparative statics, I believe that When Histories Collide simply lacks the literary elegance to have had any mass market appeal. That being said, who cares about mass market appeal? I don't. When Histories Collide is larded with just the type of data which keeps you turning the page.

Of course, data isn't the only item on the menu here, as an economist Crotty brings some noticeable theoretical baggage. His central thesis is that the rise of individualistic capitalism in West Central Europe¹ is sui generis, as distinct from hunter-gatherer, pastoralist and Asiatic modes of production (he uses the term riverine agriculture, but it's pretty clear that most people would recognize this as Asiatic mode of production). Additionally, there are a few other types, such as the slave based individualistic capitalism of the ancient Mediterranean, and the elite capitalism of post-colonial states (e.g., Latin America). Crotty's macrohistorical model as it applies to development economics is rather straightforward: individualistic capitalism emerged in a particular place and time, and the Great Divergence is a byproduct of those conditions. These means the export of this system of economic development and productivity is going to be problematic; the societies of East Asia are a particular exception because they were not colonized and so their indigenous cultural systems were not extinguished. Rather, these societies integrated Western ideas and tools in an eclectic manner in keeping with their cultural biases and strengths. Crotty labels the East Asian Tigers as "collectivist capitalism." From what little I know of East Asian economic production I don't think this is an unfair characterization, though globalization is making these typologies less relevant when transnational companies span civilizational boundaries.

Despite the editing which places the Irish material toward the end of the book it is quite clearly foreshadowed throughout the book. It is Crotty's deep case study which illustrates just how sui generis individualistic capitalism is, and how difficult, nigh, impossible, it is to export it to colonized societies which are habituated toward a different mode of production (Ireland leans towards pastoralism). Ireland, being the British nation's first large scale colony, and the longest experiment in such a relationship (lasting from the Tudor period down to 1921), is therefore ideally placed to illustrate the general dynamics. Additionally, a few particularities of Ireland such as its proximity to the colonizing country and its later assimilation into the European Economic Community bring into sharper focus the causal factors behind its deviations from the standard post-colonial narrative.

There is unfortunately an awkward problem; the Celtic Tiger. Crotty died in 1994, and he was clearly writing until the end as his statistics are up to date as of 1992. But it is also obvious that a great deal of the material draws upon the author's nearly 40 years of scholarship in the field of agricultural economics, so the echo of the Ireland of 1960 looms large. From what I can tell it seems that Crotty assumed that the economic robusticity of the Ireland of the second half of the 20th century was a credit driven mirage which would ultimately founder on the lack of institutional support; and it seemed that he believed he saw it already occurring by the early 1990s. I am well aware that there is a great deal of debate about Ireland's economic growth and how to interpret the various indices. As with much social science there is plenty of revisionism which attempts to dig out more nuance from the "first look" impressions generated by something like per capita income. I'll grant that on the margins there is something to debate, but I think it's pretty clear at least over the past 15 years Crotty was just not right about Ireland and its inability to join the other nations of Europe on their level and terms. The foreword for When Histories Collide was penned by a colleague of the author in 2001; and I felt his assessment of the Irish economy since Crotty's death was telling, as he made only the most perfunctory attempts to defend his friend's doom & gloom prognostication. It seemed implicitly to be suggesting that prediction is less critical in a work of such grand scope as When Histories Collide, at least over normal human time frames, and the insights which one might gather are still worth an examination of the full structure of the argument.²

I agree with this. Because of my general skepticism of the predictions made in When Histories Collide I will avoid detailing the Georgist prescription which Crotty offers as his ultimate plan for how to ameliorate poverty. But, I want to highlight one more systematic flaw: a general tendency toward historical sloppiness. This seems to be a major feature of economic history in general; the preoccupation with macroeconomic forces tends to sweep aside details of history to the point where falsity and misrepresentation regularly creep in. John Nye's War, Wine, and Taxes: The Political Economy of Anglo-French Trade, 1689-1900 is a nice exception to this general rule, but I suspect the rather narrow purview of this work explains the tight fidelity to reality as opposed to the standard stylized historical sketches borrowed from high school textbooks.

I will offer two examples which illustrates the weakness in the area of historical details which plague When Histories Collide. First, Crotty offers a model for the emergence of ancient Mediterranean civilization predicated on the synthesis of Indo-European pastoralists with indigenous Phoenician agriculturalists. What's the problem here? Phoenicians were a specific group of Semitic speaking peoples who flourished in what is today's Lebanon. As a colonizing people they do not pre-date ~ 1000 BCE. We know that Greek was spoken in Greece by ~1500 BCE; and likely Indo-European languages were extant on the northern shore of the Mediterranean well before 1500 BCE. Additionally, note that I stated on the northern shore of the Mediterranean, Phoenician colonies as it happened were almost all planted in non-Indo-European areas, and mostly on the south shore. By Phoenician Crotty actually means the diverse pre-Indo-European speaking substrate of the northern Mediterranean which the Greeks, Latins and other assorted peoples replaced and assimilated (some of these pre-Indo-European speakers remained down to the Roman period, e.g., Iberian).

Of course, I will admit that to some extent the error doesn't truly undermine the structure of the author's thesis: that there was a synthesis between these two broad cultural types (whatever you may term them) which resulted in the civilization of the Mediterranean. The second argument is specifically about the economic motor of the ancient Mediterranean, and I believe it to be a more telling error. In short, Crotty argues that the creativity of ancient Mediterranean capitalism was contingent upon the ubiquity of slavery. Slavery was a normal institution before the modern period; all societies had some forms of slaves, but different societies practiced slavery to different quantitative extents. The cultures of the ancient Mediterranean, specifically Greece and Rome, as well as the more recent race-based slave societies of North America and the Caribbean, are exceptional in the centrality of slavery in terms of economic production (in many societies slaves are luxuries or a trivial demographic). Though slaves were only a minority in the Roman world (around 25% of the population) Crotty argues that their economic productivity was the engine which drove the efflorescence of ancient civilization. Slaves could not consume the fruit of their own labors, so their productivity so sequestered freed up ancient elites as surplus for leisure and warfare. The structure of the argument here is plausible, but the problem is when Crotty makes the argument about where the slaves came from: the steppe. Here Crotty his going back to his history where Indo-Europeans and Phoenicians came together to produce Mediterranean civilization; the steppe is a region where the need for labor is minimal because of the pastoral lifestyles, it is land that is limiting, and so the excess population is driven into the cauldron of civilization. Here, they are enslaved and their productivity drives Mediterranean society. The problem is that it seems to me totally implausible that the steppe had a large enough population that it could ever have supplied enough human beings to replenish the constantly dying 1/4 of the Roman Empire's population which consisted of slaves. As a point of fact it seems that Northern Europeans, especially those from beyond the limes, were the primary exogenous source of slaves. But, I also have read that the Romans bred slaves on farms in Sicily, so there was also endogenous production. Crotty's argument is that when the Roman Empire reached its natural limit and was no longer sucking in slaves through wars it naturally collapsed because of the diminishing of its economic engine. I don't believe this, it oversimplifies some real complexities of the period between Augustus (the early Empire) and Late Antiquity, when the classical state collapsed. The consensus scholarship seems to be that the Roman Empire recovered from a near collapse in the 3rd century in the 4th, and though society was reconstituted so that we could see the vaguest of outlines of the medieval system already in the post-Diocletian period, it may be only that repeated exogenous shocks in the 5th century succeeded where those of the late 2nd and 3rd failed. Instead of a historical deterministic process, what we have is historical contingency which would have lead to a fall probabilistically at some point.

I've harped on the negative points of the book to this point because I don't want people to purchase this assuming that they'll get a literary tour de force on the scale of Guns, Germs and Steel; rather, When Histories Collide exhibits all the strengths and weaknesses of Farewell to Alms magnified. But what are those strengths? Here's a sample of what I think is worth reading through all the issues above for:

...Very roughly, the same pastoral resources will, in a year produce 400 gallons of milk (the yield from a mediocre cow) or 250 lbs. liveweight gain from a bullock, or ox.

The milk, which weighs roughly 10 lbs. per gallon and has about 12 percent dry matter content, gives 400 X 10 X 0.12 = 480 lbs. of digestible dry matter. The bullock liveweight gain will convert into carcass at around 55 lbs. carcass per 100 lbs. liveweight. The carcass has about 70 percent meat and fat (the balance being inedible bone), of which the dry matter content is about 50 percent. The bullock liveweight gain gives therefore 250 X 0.55 X 0.70 X 0.5 = 48 lbs. (approx.) of digestible dry matter

Thus the acquisition through natural selection under these crop-less circumstances of the ability to consume milk from other species beyond infancy and, indeed, as in the case of the Tutsi in Rwanda, to live on an almost exclusively milk diet, made it possible for more people, therefore more efficient and powerful people, to live on given pastoral resources.

Consider that. The milking of cows can increase the agricultural productivity of a unit of land by an order of magnitude! (assuming that the land is not arable) No wonder lactose tolerance swept across many populations so fast! Crotty identifies three general cow-cultures:

1) The pastoralist model

2) The South Asian model, the "apotheosis of the cow"

3) The European model; in particular, the model associated with the rise of individualistic capitalism

The pastoralist model is pretty straightforward; man have cow, man milk cow, man defend cow from enemy. This way of life puts a premium on land but requires little labor or capital inputs; you put the cattle out to pasture and make sure that they do their thing and protect them from predators and rustlers. Crotty presumes that this was the culture which arose among the Proto-Indo-Europeans on the steppe, and it is what exists among the Nilotic peoples of Africa, and also was the norm among the pre-modern Irish. The apotheosis of the cow doesn't need much description, everyone knows that South Asians (Hindus and affinal groups specifically) do not consume beef and hold the cow to be sacred. The standard economic explanation here is that cows are more efficient bundles of calories integrated over time through milk extraction than as a one time item for slaughter. But there's a twist to this in India which I only know because of Marvin Harris' Cows, Pigs, Wars, and Witches: The Riddles of Culture: the cows which wander the cities and countryside of India are generally cows, that is, female. Where are all the bulls? They're being used as draught animals! South Asian agriculture is obviously extremely intensive in labor, and cattle serve the role that water buffalo do in the moister regions of Asia (including the margins of South Asia). Crotty doesn't mention this, but I think that's another part of the puzzle. And it fits in which another datum which plays a role in the thesis of how and why individualistic capitalism arose: Indian cows need to have their young reared to give milk. Obviously you couldn't kill the calf which was the reason for the milk production.

The final cattle culture is that of Western Central Europe; the region of northern France, the Low Countries and Western Germany characterized by 3-crop rotation and draft animals with mouldboard plough by the medieval period. I can't do justice to the detail of Crotty's argument here, and to some extent I don't think it all fits together, but there are many intriguing pieces. Lactose tolerance comes into the picture because when the Proto-Indo-Europeans brought the cow and their ability to digest milk into Central Europe they opened up the possibility for a new lifestyle. Because of the low agricultural productivity in this region in regards to cereals, using these crops as fodder for cattle was attractive. Middle Eastern cereals were simply not well adapted during the early phases to the Northern European climatic regime. Additionally, low quality or unpalatable crops like oats were sometimes the only option, and these were more productively fed to cattle to convert into more palatable nutritional items (whether as milk or meat). But there's a problem here: European winters mean that there's no pasturage to keep the cattle alive through the winter. So fodder is of the essence. Because this is relatively limited Europeans would have to kill most calves so as to maximize the feed for the adult cows. After you kill an animal, of course you eat it since to do otherwise would waste valuable protein and fat, so there is no apotheosis of the cow in a society where the cow may nevertheless be a central fixture.

The production and generation of fodder for cattle by smallholders is a critical part of the story of the generation of individualistic capitalism. In short, it habituates the average person toward low time preference as an interlocking set of agricultural operations are set into motion to maintain subsistence in an ecologically marginal environment. For Crotty the "bottom up" nature of this societal shift is critical as the emphasis on capital over land or labor as the factor of production which would increase marginal product is what will lead to the takeoff of the Great Divergence thousands of years into the future. Unlike classical Mediterranean civilization Western European individualistic capitalism can weather famine, pestilience, and other exogenous shocks of God. Capital persists while slaves die. The dispersal of technological initiative through society gives it a redundant robusticity lacking in other top-down civilizations. In our modern world the power of capital in the form of technological innovation in perpetuating a world of plentitude always outrunning the Malthusian Trap is obvious, but only Central West Europe managed to hit upon that formula in the pre-modern world because of the confluence of particular ecological and cultural parameters at a particular moment in time. Crotty argues that the capital intensive post-Malthusian Developed World was not inevitable, but a contingent fact of history.

Ecological constraints play a large role in explaining why Ireland is different in this model; the mildness of Ireland's maritime regime means that winter fodder is unnecessary. Transhumance and semi-pastoralism is feasible in this scenario; and, critically it is important to note that pre-modern Irish cattle were more like their South Asian cousins than continent European lineages. They only gave milk when with calf! The selection process whereby only the best milk producing lineages were kept and most calves killed in the fall did not apply to Ireland. From this ecological difference flows the great differences between the folkways of the Irish and those of peoples to the East. Speaking of which, When Histories Collide takes occasional forays into Eastern Europe, where it is explained that autocratic capitalism developed along the Slavic frontier. Here obviously land was not limited, and labor was at a premium, but capital intensive methods from the West could be introduced periodically to push the frontiner outward. By the time of the gunpowder empires the steppe ascendency in terms of arms was finally banished and a synergistic alliance of peasants (labor) and boyars (capital) swept across the land. But the fundamental distribution of techniques remained distinct from those of Western Europe, where technological innovation bubbled up from below rather than horizontally via elites. In the north, in Scandinavia, the local human capital was well equipped to leverage the horizontally transmitted suite of the Western European economic system, replicating individualistic capitalism once the technological wavefront had pushed far enough to overcome ecological hurdles.

Obviously this is only a small slice of the arguments presented in Raymond Crotty's magnum opus, but it's a representative taste. Clearly I think there are some serious issues with the depth of the scholarship on the margins, but the details of history which I think are rather embarrassing in the ignorance that they bespeak is not entirely out of place in the corpus of economic history. That being said, as I noted above some of the arguments about the slave-based individualistic capitalism of the ancient Mediterrean are premised on unrealistic assumptions which derive directly from the lack of a dense network of historical priors. Crotty's analytic tools were ones of mathematical economics, and his empirical database was one of agricultural economics, in particular Irish agricultural econometrics and history. The limits to his disciplinary horizons often shows. Nevertheless, I don't believe that Crotty falsified the tables or the quantitative data he repeats, and those alone are worth perusing this book. Who knew that for most of history the per unit productivity of agriculture in China was about twice that of South Asia? Crotty did, and I didn't. I don't think that the grand theoretical arguments should be taken without some major salting and curing; as I said recent history seems to have proved him wrong in Ireland, and to a lesser extent the post-colonial world as a whole. His model of the past has great descriptive flaws and would have been better served with a more robust cliometric framework. But by & large When Histories Collide is a good complement to more polished recent works such as Farewell to Alms and The Great Divergence.

Related: 10 Questions for Greg Clark, A World of Difference: Richard Lynn Maps World Intelligence, Group lifespan differences? Maybe it's agriculture and The Horse, the Wheel, and Language: How Bronze-Age Riders from the Eurasian Steppes Shaped the Modern World. Do note that Amazon is telling me that those who purchased When Histories Collide also bought The Horse, the Wheel, and Language: How Bronze-Age Riders from the Eurasian Steppes Shaped the Modern World. Not surprising, but shows the general slant of Crotty's macrohistory.

1 - By West Central Europe one can imagine the lands which are just to the West and East of the Rhine; northern France, the Low Countries and western Germany.

2 - Crotty also asserts that post-colonial poverty will increase in the future do the poor fit between individualistic capitalism and most societies. I think on the balance Crotty has again been proven wrong; even removing China from the equation it seems that on the whole the world has not seen economic retrogression with the possible exception of large swaths of Africa. Despite the Asian flu of '98 and rollback from the Washington Consensus, both Southeast Asia and Latin America seem to be better off than they were a generation ago.

Labels: Economics, History

While I'm recommending weblogs you might not have heard about, check out Mailund on the Internet. The tag line is "computer science, bioinformatics, genetics, and everything in between." For a taste, here are his posts on association metholodiges.

Labels: Genetics

My friend Jake Young has a post up, Contrasting Views on the Gender Disparity in Science:

Second, one of my primary arguments against innate differences in ability between men and women is that you are dealing with traits that have distributions and those distributions largely overlap. Making a statement about any individual man or woman is largely useless. The odds of a women or man selected at random being better or worse at math are not particularly different. This argument applies just as well to differences in preference. Maybe there are differences on average, but they are still distributions that overlap. The key question becomes: to what degree do those distributions overlap? How different on men's and women's preferences on average?

James Crow's Unequal by nature: a geneticist's perspective on human differences is apropos here:

There is actually a simple explanation that is well known to geneticists and statisticians, but not widely understood by the general public or, for that matter, by political leaders. Consider a quantitative trait that is distributed according to the normal, bell-shaped curve. IQ can serve as an example. About one person in 750 has an iq of 148 or higher. In a population with an average of about 108 rather than 100, hardly a noticeable difference, about 5 times as many will be in this high range. In a population averaging 8 points lower, there will be about 6 times fewer. A small difference of 8 points in the mean translates to severalfold differences in the extremes.

...

My conclusion, to repeat, is that whenever a society singles out individuals who are outstanding or unusual in any way, the statistical contrast between means and extremes comes to the fore. I think that recognizing this can eventually only help politicians and social policymakers.

Labels: human biodiversity

Several of my previous notes have touched on the subject of Sewall Wright's F-statistics. The best known of these is FST, which is very widely used as a measure of the genetic divergence between sub-populations of a species. My aim in this note is to trace the evolution of the F-statistics in Wright's work.


Why F?

A preliminary question is one of terminology. What, if anything, does the letter 'F' stand for? One plausible answer is that it stands for 'fixation', since among other things the F-statistics can be used to measure the rate at which alleles tend to be 'fixed'. Wright himself in his later writings sometimes refers to F as an 'index of fixation'.

Plausible though this may be, it does not seem to be the origin of Wright's use of the letter F. This first appeared in his series of papers on 'Systems of Mating' in 1921, where he uses the letter F (in its lower-case form 'f') as a symbol for the 'correlation between uniting gametes' and as a measure of inbreeding. Although the word 'fixation' does occur in these papers, Wright does not say that 'f' stands for 'fixation'. The banal truth seems to be that by the time Wright needed a symbol to represent the correlation between uniting gametes, the letters a to e had already been allocated to other purposes, so that f was the first available letter in the alphabet.

F as correlation between uniting gametes

Wright's primary use of F (or f) is to designate the correlation between uniting gametes. The general idea of a correlation between gametes is now somewhat unfamiliar. If there are varying types of gametes in the population, uniting gametes may be said to be positively correlated if the same types tend to be paired together at mating, or negatively correlated if dissimilar types are paired. If the different alleles at a locus in the population are given notional numerical values, such as 0 and 1, a correlation coefficient for the correlation between pairs of uniting gametes can be calculated in the usual way. (For a fuller explanation see my post on Wright's measurement of kinship.) The resulting correlation coefficient is F.


Heterozygosis and the correlation between gametes

Also in 1921 Wright points out that the correlation between uniting gametes is connected with the proportion of heterozygotes in the population. Whether an individual is heterozygous at a locus is determined by the gametes (egg and sperm) of its parents which unite to form a zygote at fertilization. If they are identical at that locus, the offspring is homozygous, otherwise it is heterozygous. The proportion of heterozygotes (the level of heterozygosis) among the offspring, over and above the level expected with random mating, can be calculated from the correlation between uniting gametes, and vice versa. In SM1 Wright calculates that the percentage of heterozygosis is (1/2)(1 - f), where f is the correlation between uniting gametes. (This is stated without full proof, but I have checked it, calculating the correlation by the method of notional values.) This formula is only valid for the special case where there are two alleles with equal proportions of 1/2 in the population, but Wright soon (in 1922) generalised it to the case of two alleles with proportions of p and q = (1 - p), in which case the formula is 2pq(1 - f). He also began to use upper-case F, rather than f, as his preferred notation.

F as a measure of inbreeding in a population

A positive correlation between uniting gametes can arise in two ways (apart from mere sampling error): by assortative mating between similar phenotypes, or by mating between genetic relatives, in other words by inbreeding. Wright deals with both inbreeding and assortative mating, but gives more attention to inbreeding. If assortative mating is excluded, then F can be used as a measure of the average degree of inbreeding in a population.

If the correlation between gametes is due solely to inbreeding, then the formula 2pq(1 - F) for the percentage of heterozygosis in a population can be given a simple interpretation in terms of Malecot's concept of Identity by Descent. The two genes at a locus in an individual are either Identical by Descent (IBD) from a common ancestor, or they are, by assumption, drawn randomly from the gene pool. In the first case they are certainly identical. In the second case, applying the familiar Hardy-Weinberg formula, they have a probability of (1 - 2pq) of being identical. Therefore if we interpret F as the probability that the two genes are IBD, on average for the population, the total probability that they are identical is F + (1 - F)(1 - 2pq) = 1 - 2pq(1 - F). Subtracting this from 1 to get the probability of heterozygosity we get the required formula 2pq(1 - F).

F and the inbreeding of individuals

The degree of inbreeding in a class of individuals (e.g. all offspring of matings between siblings) can be derived from an analysis of the way in which they are bred. The coefficient of inbreeding then measures the correlation between any pair of alleles at the same locus in an individual belonging to that class.

The level of inbreeding in an offspring can be derived from the correlation between the uniting gametes of its parents, which in turn can be derived from the correlation between the parents themselves, in accordance with Wright's method of path analysis. The full method would involve considerations of dominance, heritability, and so on, but the coefficient of inbreeding is usually derived using a simplified method devised by Wright himself and expounded in several papers of the early 1920s (see especially paper 2 in ESP).

In the simplest case, for the offspring of half-siblings who are not themselves inbred, Wright's formula gives a coefficient of inbreeding of 1/8. This is the same as the figure derived by the methods of Malecot for the probability in this case that the two genes at a locus in the offspring are identical by descent. In Malecot's approach this result is derived from explicit assumptions about probabilities. It is assumed that each gene in an offspring has a probability of 1/2 of coming from either parent, and - very importantly - that there is an independent probability of 1/2 that the same gene is inherited by any other offspring of the same parent. This is an assumption which is usually empirically correct (with certain exceptions such as sex chromosomes), but it is not logically necessary. For example, if surviving offspring came in pairs, each member of which received genes from complementary chromosomes in the parent, such pairs of offspring would have a lower correlation with each other than the usual calculations would suggest.

It is therefore worth asking what features of Wright's approach take the place of the explicit probability assumptions in Malecot's system. The first key assumption, that each gene in an offspring has a probability of 1/2 of coming from either parent, is explicitly stated as a biological assumption (with the exception of sex-linked genes) in Wright's derivation of the path coefficient between offspring and parent. The other key assumption, that there is an independent probability of 1/2 that the same gene is inherited by any other offspring, does not seem to be explicitly stated. In SM1 Wright only directly calculates the correlation between parent and offspring. All other correlations, such as those between siblings, are derived indirectly from the parent-offspring correlation by the method of path analysis. The assumption of independent probabilities for each offspring seems to be built into the general assumptions of path analysis. In a late discussion of the principles of path analysis Wright emphasised that 'The validity of the system requires that any variable that enters into the system as a common factor back of two or more dependent variables, or as an intermediary in a chain, vary as a whole. If one part of a composite variable.... is more significant in one relation than in another, the treatment of the variable as if it were a unit may lead to grossly erroneous results' (EGP vol. 1 p.300). Fortunately, the assumption appears to be consistent with the usual pattern of genetic inheritance. Apart from special cases such as sex-linked genes, or MZ twins, it seems that each surviving offspring has an equal and independent probability of receiving any given allele from the same parent. This is despite the fact that during the formation of gametes the precursor-cells of the gametes are formed in pairs with complementary alleles from different chromosomes in the parent. In the case of eggs, only one of the proto-eggs formed from the same parental cell usually survives. In the case of sperms, so many sperms are produced in total that the chance of two sperms derived from the same parental cell both ending up in surviving offspring is negligible.

F as a measure of inbreeding relative to a foundation stock

One of Wright's original motives in devising his F statistics was to measure the effect of continued inbreeding over a number of generations. In agricultural (and laboratory) practice it is common for animals to be bred systematically over long periods using close relatives, e.g. mating sisters with brothers, or daughters with their fathers. With such practices the level of inbreeding among the offspring rises over the generations, and the level of heterozygosis declines. Wright's F-statistics provide a convenient method of measuring this process, superior to the previous ad hoc methods. The result of a number of generations of inbreeding within an inbred line can be summarised in the average F within that line, relative to the foundation stock (the population from which the inbred line is derived). The cumulative decline of heterozygosis since the inception of the line can then be calculated using the formula 2pq(1 - F). But this should raise questions about the precise meaning of F in such a case. F is in principle always a correlation coefficient, and could if necessary be expressed in terms of the Pearson product-moment formula. This requires the mean and standard deviation of the relevant statistical population to be specified. But what is the mean in the present case? The correlation is said to be 'relative to the foundation stock', so this appears to be the relevant statistical population, but the foundation stock no longer exists, and the correlated pairs are not part of it. So what is going on? Is F a legitimate correlation coefficient at all when more than one generation is involved?

This puzzled me until I paid proper attention to page 169 of SM5. This gives the key to the mystery. Rather than just considering the correlation within a single inbred line, we must consider an indefinitely large (actual or hypothetical) ensemble of lines, all separately inbred according to the same system (e.g. sibling mating) for the same number of generations, and all derived from the same 'foundation stock'. The mean gene frequencies for the entire ensemble (or a large random sample thereof) should then be the same as in the foundation stock (in the absence of selection and mutation), but will vary within each particular inbred line according to the chance variations resulting from the reproductive process. F will therefore measure the average correlation within each such line as compared with the values of the foundation stock. Such a correlation coefficient will usually be hypothetical, since no such ensemble actually exists, but in principle it has a clear meaning consistent with the general method of correlation.

The story so far

The uses of F (or f) identified so far were all first described in Wright's ground-breaking 'Systems of Mating' in 1921. The different uses therefore cannot be put in a chronological sequence. Logically, however, the sequence is as follows:

a) F as the correlation between uniting gametes. This is always the fundamental conception.

b) F as a measure of average inbreeding in a population. In this sense it is closely connected to the level of heterozygosis.

c) F as a measure of inbreeding in an individual. In this sense it is closely connected to the measurement of relatedness.

d) F as a measure of continued inbreeding in a line relative to a foundation stock - see the last paragraph.

F in natural populations

As developed by Wright in 1921, the concept of F was heavily influenced by the circumstances of agricultural stock breeding, where mating is carried out in accordance with some deliberate plan. (Wright was employed in agricultural research for the US Department of Agriculture at the time - see Provine, chapter 4). The next major step was Wright's application of F to the measurement of genetic drift in natural random-mating populations. It is clear from Provine's biography that Wright first took this step around 1925, but the results were not fully published until the major paper on 'Evolution in Mendelian Populations' in 1931.

I have discussed genetic drift in a previous post, and will not repeat that discussion here. The essential point is that in any finite population, over the course of time, there will be a tendency, purely by chance, for some lines of ancestry to be relatively successful, while others dwindle and eventually die out. The result is that, in the absence of selection or mutation, fewer alleles will account for a larger proportion of genes in the population, and the level of heterozygosis will decline.


As a result of genetic drift, F tends to increase at a rate of approximately 1/2N per generation, where N is the size (strictly, the 'effective' size) of the random mating population. But F is still in principle the correlation between uniting gametes. Since the correlation between uniting gametes within a random mating population is zero, how can there be an increasing value of F?

The answer is again that F is a correlation relative to the baseline of a 'foundation stock'. Wright does not, so far as I know, explain what exactly this means in the case of a natural random mating population, but I think we can understand it by analogy with the case of inbred agricultural breeding lines. We are to imagine that from a specified generation onwards a population is allowed to evolve by random genetic drift in a large number of hypothetical different ways. Within each of the resulting hypothetical descendent populations there will be a correlation between uniting gametes relative to the entire ensemble of hypothetical outcomes. The average of these correlations is constantly increasing. It is conceivable that in some cases the actual observed value of F - the correlation between uniting gametes within an actual population relative to that in the foundation stock - would be negative, but the expected average F is always positive.

F in subdivided populations

If a number of subgroups of a population breed within themselves in full or partial isolation from each other, the gene frequencies within them will tend to diverge from each other as a result of selection or genetic drift. Within each such subgroup, individuals will tend to be more similar to each other than to individuals randomly selected from other subgroups or from the entire population. Within the groups, individuals will therefore be positively correlated with each other relative to the entire population.

Wright developed a system of F-statistics to analyse the structure of subdivided populations. This is one of his major contributions to population genetics after the fundamental paper EMP of 1931. The best-known of the F-statistics is FST, where S and T should ideally be subscripts, and stand for 'subpopulation' and 'total population'. The expression FST is possibly first used in a paper of 1950 (ESP p.585), but the underlying concept was first developed in a paper of 1943 on 'Isolation by Distance'. (I will cite this from the reprint in ESP, but it may be available online here. I downloaded it successfully once, but on another occasion got an error message.)

Wright considers a population subdivided into a number of subpopulations of equal size, within which mating is random, and with two alleles at a locus. He shows, by a relatively simple but ingenious proof (ESP p.403), that in this case the correlation between uniting gametes within each subpopulation, relative to the total, is equivalent to Vp/pq, where Vp is the variance of the gene frequencies of the subpopulations (i.e. the mean square of their deviations from the frequency in the total population), and p and q are the frequencies in the total population. In 1943 this correlation is simply called F, but it is in fact the measure later known as FST. Wright recommends that the square root of F could usefully be taken as a measure of the genetic divergence between populations. (Of course, the rank order will be the same whether we take F itself or its square root as the measure.) It may also be noted that Vp/pq cannot be negative, as both the numerator and denominator are necessarily positive or at least zero. In general, a correlation coefficient may be either positive or negative, but in this case F measures the correlation due to the average differences between the gene frequencies of subpopulations, regardless of sign, and these cannot be less than zero.

In the same 1943 paper, and in subsequent papers of the 1940s, Wright developed methods for dealing with correlations within hierarchically subdivided populations, where mating within each division may or may not be random. His terminology varied somewhat, but by 1950 he seems to have settled on the following (with IT, IS, and ST as subscripts):

FIT: inbreeding coefficient of individuals relative to the total population
FIS: inbreeding coefficient of individuals relative to the subpopulation
FST: correlation between random gametes drawn from the subpopulation relative to the total population. (If mating is in fact not random within the subpopulation, this is a hypothetical correlation.)

Wright shows that these measures are related by the equation FST = (FIT - FIS)/(1 - FIS). (For a relatively simple proof see EGP vol. 2 p.294-5, but note that the left square bracket in Equation 12.14 on that page is in the wrong place: it should be immediately before the first occurrence of qT.) It may be seen that if FIS is zero, in other words if mating within subpopulations is random, then FST = FIT. This is as it should be, since in this case the only source of correlation between individuals is the division of the population into subpopulations. FST then accounts for the entirety of the correlation within the total population, which is FIT.

Wright's F-statistics are still widely used or alluded to, but are seldom understood in their original sense as correlation coefficients. Inbreeding within individuals is now usually explained by means of Malecot's Identity by Descent, while FST is usually explained in a way more appropriate to Masatoshi Nei's GST. Wright's work was however clearly the inspiration and foundation for the work of these later geneticists.

A few cautions about the use of FST may be useful.

a) Wright originally intended FST to be calculated as an average over a large number of subpopulations. In theory, it would be possible to calculate it for as few as two subpopulations, in which case, if they are of equal size, FST is d^2/pq, where d is the deviation of the subpopulation frequencies from the frequency in the total population. So far as I know, Wright himself never used it in this way.

b) FST is calculated from gene frequencies on a locus-by-locus basis. It may well vary from one locus to another. To get an indication of the extent of evolutionary divergence between subpopulations, it is desirable to take the average FST over a large number of loci.

c) FST is not simply proportional to the length of time or number of generations that two subpopulations have been diverging. Other factors such as the amount of migration between them and the size of the populations are also relevant. Small populations diverge by genetic drift far more quickly than large ones.

d) Wright intended FST mainly to be used for genes that are not subject to significant natural selection. Genes that are under selection may diverge either more or less in different subpopulations than an average FST would suggest.


References:

William B. Provine: Sewall Wright and Evolutionary Biology, 1986.

Sewall Wright: Evolution: Selected Papers, edited and with Introductory Materials by William B. Provine, 1986. (ESP)

Sewall Wright: Evolution and the genetics of populations, 4 vols., 1968-1978. (EGP)

Labels: Burbridge, Population genetics

Think Gene points me to a new PNAS paper, Structure of TRPV1 channel revealed by electron cryomicroscopy:

The transient receptor potential (TRP) family of ion channels participate in many signaling pathways. TRPV1 functions as a molecular integrator of noxious stimuli, including heat, low pH, and chemical ligands. Here, we report the 3D structure of full-length rat TRPV1 channel expressed in the yeast Saccharomyces cerevisiae and purified by immunoaffinity chromatography. We demonstrate that the recombinant purified TRPV1 channel retains its structural and functional integrity and is suitable for structural analysis. The 19-A structure of TRPV1 determined by using single-particle electron cryomicroscopy exhibits fourfold symmetry and comprises two distinct regions: a large open basket-like domain, likely corresponding to the cytoplasmic N- and C-terminal portions, and a more compact domain, corresponding to the transmembrane portion. The assignment of transmembrane and cytoplasmic regions was supported by fitting crystal structures of the structurally homologous Kv1.2 channel and isolated TRPV1 ankyrin repeats into the TRPV1 structure.

Think Gene and Scientific Blogging have summaries of the paper. Proteins are great, but what about the genes which produce them? I went to haplotter, and check out what I found....

iHS


D



Screenshot of genes around TRPV1


Also check out variation around that gene.

Related: Genetics of taste.

Labels: Genetics

Pigementation is turning out to be one of the most tractable phenotypes for genome-wide association studies-- a new paper from Decode identifies another couple loci that influence various aspects of hair and skin pigment. These add to the growing list of pigmentation genes in Europeans--I've not done the math, but these loci must account for some sizeable chunk of the total genetic variance in these traits.

Why has pigmentation been so amenable to mapping, while other traits like height, weight, or most diseases hover at about 2-3% of the variance explained? One possibility is that it's because pigmentation has been subject to strong recent selection--theory predicts that the initial moves toward an new fitness optimum will be loci of large effects, while the later moves will be smaller. Perhaps since this selective pressure has been so recent, we're still picking up those initial mutations of large effect that are still segregating in the population?

Labels: Genetics, Pigmentation

Genes For Musical Aptitude In Finnish Families Located:

Researchers from Finland and USA have identified one major and several potential loci associated with musical aptitude in the human genome. The results raise an interesting question about common evolutionary background of music and language faculties.

The paper is open access, Genome wide linkage scan for loci of musical aptitude in Finnish families:Evidence for a major locus at 4q22:

The heritability estimates were 42% for KMT, 57% for SP, 21% for ST and 48% for the combined music test scores. Significant evidence of linkage was obtained on chromosome 4q22 (LOD 3.33) and suggestive evidence of linkage at 8q13-21 (LOD 2.29) with the combined music test scores using variance component (VC) linkage analyses. The major contribution for the 4q22 locus was obtained with KMT (LOD 2.91). Interestingly, a positive LOD score of 1.69 was shown at 18q, a region previously linked to dyslexia (DYX6), using combined music test scores.

Labels: Genetics

I came across an interesting 2007 talk that social psychologist Roy Baumeister gave to the American Psychological Association, "Is There Anything Good About Men?" He informally reviews the literature on sex differences in ability and motivation. Some of it will be old news for readers, such as the discussion of Larry Summers, but there's quite a lot that will not. Some interesting tidbits:

- Most people in the West now believe that women possess more desirable qualities than men do. (Agreed -- I only interact with males as colleagues, keeping all of my friends female.)

- Women are more likely than men to commit violence against an intimate partner.

- About 80% of those who work 50-hour weeks are men.

- 93% of those killed on the job in the US are men.

- Men appear more oriented toward large-scale social groups where relationships are shallow but many, women toward small-scale groups where they are deep but few. Baumeister suggests that this is a key source of male-female inequality after the transition to agriculture: men were more suited to the large-scale networks that came to run social, political, and economic life.

Labels: Psychology, sex differences

In the comments section to a 2blowhards post on booty shakin', blogger Alias Clio puts forth an argument from incredulity regarding several hypotheses I proposed: 1) that male preferences for different parts of the female body have, over time, correlated with personality traits; 2) that natural selection has had a role in causing some men to prefer one body part over another; and 3) that the correlation could be caused by some simple mechanism. She also repeats an evolutionary just-so story about why human females developed large breasts -- that is has something to do with face-to-face sex -- and that too is worth taking a hard look at (the story, that is).

As to 1), the available data do paint a somewhat clear picture that assmen, boobmen, and legmen are not the same on average for personality traits. What Clio doubts is that the correlations here and now can be projected back into the past or into other parts of the world. That's true enough, but it's true of anything psychological, and only for technical reasons: when we discover which gene variants in males are implicated in preferring T over A, we can dig up or unfreeze ancient humans, sequence their DNA, and see if the males were boobmen or assmen. That's how we found out that some Neanderthals were probably red-headed, despite the fossil evidence not telling us anything about their hair color.

Though everyone knows it's a dubious move, the best we can do to see what preferences may have been like in sub-Saharan Africa 100,000 years ago is to investigate present-day hunter-gatherers in Africa. The Hadza are a well studied hunter-gatherer group who live in Tanzania, and a study by Marlowe et al. (2005) (free PDF) shows that Hadza males prefer females who have a low waist-to-hip ratio in profile (i.e. due to protruding buttocks), rather than from the front (i.e. an hourglass or wasp-waist shape), while Western males prefer the converse. The authors did not collect personality data on the Hadza males, and did not test to see whether a male preferred boobs or buttocks, but in principle this would not be difficult to do, and we could see whether a similar pattern showed up among African hunter-gatherers.

That brings us to 2), whether or not natural selection had a role in the emergence of boobmen. Clearly they are a new morph within homo sapiens. They are too high in frequency to be the result of de novo mutations here and now, and they did not all migrate from some pre-historic Martian colony of homo sapiens. That leaves genetic drift or natural selection. Genetic drift can cause allele frequencies to go up or down over time, but it cannot produce design. Mate preferences are too specific and coordinated during development to admit a believable drift explanation: natural selection appears to have fashioned them.

But toward what end? We don't need to know, really. With the completion of the HapMap project, we are learning of tons of cases of natural selection in human beings, and we largely have no clue what it was up to. The numbers don't lie. Still, let's indulge in a little conjecture just to show that the idea isn't so perplexing in the case of boobmen.

In many areas of life, there is no one best solution, and we face a trade-off. If I develop conspicuous ornaments, that may make me more attractive to females, but it may also give me away to predators more easily, or provoke the envy of duller looking males, who might ostracize me (no small matter in a social species). Duller looking males might avoid predators and envy-based ostracism, and may be able to work better in groups because of this, but they won't be as attractive physically to females. The result is that some fraction of males will be dull and the rest conspicuous. We would need tools from game theory and differential equation modeling to spell out what parameters are involved, and what the exact frequency of each would be at equilibrium. But the point is that neither is universally favored, so both will co-exist.

So it could be with boobmen and assmen. I don't think these preferences per se were the target of selection, but again that they correlate with other personality traits that have been under selection. For instance, everyone says that compared to boobmen, assmen are more likely to have polygynous tendencies, to prefer short-term relationships, and to emphasize female qualities most relevant to the short-term (such as her most sexual body part, the derriere). We don't know if that's true, but it would be surprising if everyone had the same specific delusion. Since both short-term and long-term strategies have pros and cons, both could co-exist.

If being a boobman is linked to a more monogamous orientation, we are asking how natural selection could have driven up the frequency of monogamous males in societies where boobmen are common, such as Northern Europe. Maybe agriculture there requires the father to stick around and provide for his kids, whereas in parts of sub-Saharan Africa where farming has lower energy requirements, females can farm on their own and not worry about whether the father will stay with her. I don't claim that this is the only way it could have happened; this example is just to illustrate how simple the process can be.

Turning to 3), the mechanism does not have to be known in order to talk about the adaptive value of the trait (see Niko Tinbergen's Four Why's for clarification). We know that lighter eyes were selected for in Europeans, but we could know this fact even if we didn't know what biochemical pathways are involved in eye color. Still, let's indulge in a little more conjecture just to show how non-mysterious the mechanism can be. It may be as simple as testosterone level, with assmen having higher T than boobmen.

This is an incredibly easy hypothesis to study empirically, though from Googling it looks like no one has done so. To repeat a finding from the boobman, assman, and legman study, though, the assmen and those who prefer both large breasts and large buttocks have more ambitious personalities and are Type-A businessmen. We also know that in various species, such as the dark-eyed Junco, higher testosterone makes a male more polygynous and less likely to stick around to help raise the kids. Whatever the mechanism turns out to be, investigating the matter is not so perplexing that we don't even know where to start looking.

Last, let's examine some very popular but utterly ridiculous hypotheses for why human females evolved large breasts, summarized here. First of all, it is not true that human females have large breasts -- some have small, some medium, and some large. Look at the picture of the chimp in that summary -- you see human females with breasts that small (or large) all the time. This is not hairsplitting: it suggests that breast size reflects some trade-off.

For example, the trade-off could be in fat deposition: if you have a fixed amount of fat and want to be conspicuous, you had better put the bulk of it in one place or the other. Only gifted (or cursed) females have so much to go around that they can have large breasts and large asses. Those who put it in their chests are probably pursuing a long-term mating strategy, and those who put it in their behinds are probably pursuing a short-term strategy, on the assumption that female supply has evolved to meet male demand.

The evolution of breasts has nothing to do with mimicry of the buttocks -- can you think of any other way that a man might view buttocks-resembling things on a woman if he wanted to? Moreover, do assmen respond at all similarly to boobs as to the buttocks? This hypothesis predicts that they should be roughly interchangeable, but I don't even notice who has big or small boobs unless someone points it out to me, and I have no way of judging what "good boobs" look like, according to boobmen. It also has nothing to do with our species' face-to-face sexual position -- again, can you think of any other way a man might look at buttocks-resembling things while having sex? And as misleading as the name may be, doggy-style is not a trait that humans have lost, like a coat of body fur.

Neither does it have to do with our bipedal posture: it's true that this posture would have obscured any rump swellings (as chimps have), but the fleshy buttocks have still been in plain view ever since -- and typically, more viewable from afar than the breasts, as they take up more volume. Five-hundred years from now, the scientific consensus will be that invoking bipedal posture as a driver of some clearly unrelated change was the 20th century equivalent of ancient Greek theories about trepidation of the spheres.

Since such hypotheses are so easily debunked, why have they persisted for as long as they have? Napoleon said that you should never attribute to malice that which can be explained by incompetence, and here the incompetence surely stems from the majority of researchers and commentators in this area being boobmen, legmen, or women. (Women will grudgingly admit that boobs and legs can be things of beauty, but recoil in disgust upon pondering the booty.) We all have a tendency to extrapolate from the personal to the universal, but when I find out that someone thinks or behaves differently than I do, I ask what forces could cause them to think or behave in such deviant ways. That's how you get a clearer picture of how the world works, but it relies on there being a diversity of views within the field. It's about time some assmen joined the ranks of sex researchers to set the field straight.

Labels: babes and hunks, Human Evolution

A Genome-Wide Association Study Identifies Novel Alleles Associated with Hair Color and Skin Pigmentation:

It has been a longstanding hypothesis that human pigmentation is tightly regulated by genetic variation. However, very few genes have been identified that contain common genetic variants associated with human pigmentation. We scanned the genome for genetic variants associated with natural hair color and other pigmentary characteristics in a multi-stage study of more than 10,000 men and women of European ancestry from the United States and Australia. We identified IRF4 and SLC24A4 as loci highly associated with hair color, along with three other regions encompassing known pigmentation genes. Further work is needed to identify the causal variants at these loci. Improved understanding of the genetic determinants of human pigmentation may help identify the molecular mechanisms of pigmentation-associated conditions such as the tanning response and skin cancers.

....Taken together, these four regions explain approximately 21.9% of the residual variation in hair color (black-blond) after adjusting for the top four principal components of genetic variation. (Conversely, after adjusting for these four regions, the top four principal components of genetic variation explain 2.6% of the residual variation in hair color.)....

There are four regions because areas around HERC2/OCA2 and MAPT showed signals. MAPT is also known as AIM1 and SLC45A2, so this makes 3 genes of the potassium-dependent sodium/calcium exchangers implicated in pigmentation (the other is SLC24A5 obviously). They adjusted for the components of genetic variation so as not to be confounded by population stratification (i.e., there was some ethnic variation among their whites and so you don't have a random mating population).

It's in PLOS; you can read the whole thing, etc.

Related: Why white people are so colorful!. Sandy also comments.

Labels: Genetics, Pigmentation

Austin Bramwell, Who Are We?:

Whatever the difficulties of conservatism, surely one can improve upon the typical performance of those who take it upon themselves to explain it. In place of the conventional accounts, try this one: Conservatism is the defense of legitimacy wherever it happens to exist. "Legitimacy" here is defined in the empirical, Weberian sense: that is, an institution is legitimate if and only if the opinion has become widespread that it is right (for whatever reason or lack thereof) to obey it. The conservative, in short, cultivates obedience to existing institutions. This definition, I submit, has all the advantages of the conventional definitions, none of their defects, and some important advantages of its own.

To some extent I think one might make the case that Liberalism is the inverse of Bramwell's definition of Conservatism; what was Liberal in 1920 might be viewed as quite Illiberal today, and what is Liberal in 2008 may seem rather Illiberal in 2028. In any case, I would add that though I don't agree with Bramwell much of the time I'm always impressed with the breadth of his erudition and his good faith attempt to argue rather than scream. Unfortunately most political and social commentary is much closer to the level of morons like Kevin James. Even when one dodges the rank stupidity of someone like James the "punditry" on offer is generally grounded in the incestuous circle-jerk of CW as opposed to facts.

Back to Bramwell's point, if you read this blog regularly you know that I have an amateur interest in antiquity, particularly the period of the Roman Empire. Today we assume that Christianity and the Christian clergy are the Conservative party at prayer.¹ But if you focus on the 4th and 5th centuries, when Christianity went from being a marginalized sect to the established Church of the Empire, you encounter the fact that the Christian religion was fundamentally one perceived as radical and deeply undermining the legitimacy of the ancients (who were pagans after all).² In the late 4th century you have powerful pagans such as Symmachus making arguments defending tolerance and subsidy for the ancient faith based on reverence for the institutions and precedents of the past and the ancestors. Fundamentally deeply Conservative reasoning arguing for the legitimacy of what has become before. By the late 5th century the pagan historian Zosimus had become quite dyspeptic toward the new dispensation, bemoaning the fall of the older order and observing the decline of his civilization all around him due to the abandonment of the old gods (Zosimus flourished in the years following the Western Empire's fall). To a great extent Zosimus reminds me of modern Conservatives of a Christian bent, who seem pessimistic by constitution when observing the decline of Christendom and the repudiation of its truths.

Today I would suspect that post-Christian Liberals would not necessarily align themselves with radicals for change such as St. Ambrose or rationalist refuters of the relevance of the pagan past such as St. Jerome; rather, their sentiments might be with the pagans who were on the losing end of the march of history because of their current quarrels with Christianity. Similarly, of course Conservatives in the West who are Christian or Christian sympathetic would admire the pugnacity of St. Ambrose and other Church Fathers in overturning thousand year old traditions & customs. The axioms of Christianity made such a rejection of the past eminently rational. And yet if temperament was the guide toward affinity I do not think that this would hold. Church Fathers who admitted pagan learning into the canon offered reasons of utility, as such wisdom might be useful toward Christian ends. A convinced pagan would not have to make such an argument because the classical canon was simply part of the customary education of the non-Christian elite; it was received tradition which needed no reflective analysis and justification. In the 4th century Christian intellectuals dreamed of a new world transformed and shorn of the dead weight of the past with its irrational and unnecessary traditions. Nearly two thousand years later the shoe is on the other foot....

1 - Despite the emergence of Leftish Christian movements such as Christian Socialism or the Social Gospel, I think one can make a strong case that on the balance Christianity has been more associated with Conservatism than Liberalism since the French Revolution and the emergence of a modern politics.

2 - Obviously the influx of classically educated men such as St. Augustine and the Hellenic patina which accrued to the religion moderates this judgement.

Labels: politics

About 5 years ago William Gunn was about to start blogging at Gene Expression; but life intervened and it never happened. Well, he's started posting at his own blog regularly, Synthesis, and I recommend it for anyone's RSS feed (you already have it if you are subscribed to The DNA Network, a really great way to introduce yourself to the "genetic blogosphere"; boy have things changed since 2002!).

Over the past few days I've heard some coverage of the horrible earthquake in China, and the anguish of the parents whose children were lost as schools collapsed. I was struck when one reporter noted that for many of the parents this was their only child.... That got me thinking about the implications of the one child policy, which is now approaching its 30th year. Most of you who read this weblog know that I think that the Bare Branches argument is a serious one; in short, that the sex imbalance within China due to son-preference will result in social instability. But what about the fact that for so many older Chinese they have only one child to support them in the future? Obviously the greying of the Chinese population is something to keep in mind when we postulate the path of the power of the People's Republic; China's active workforce will start to shrink in the near future, while its dependent class will increase in proportion. But in terms of the irratonal bellicosity which is par for the course for ascendent powers attempting to stake out a place in the sun...I wonder how eager the Chinese will be to send their sons abroad if so many of them are their only sons? Does anyone know of any social science correlating levels of international conflict with TFR? There are obviously angles to analyze this problem theoretically via social evolution, assuming that each offspring is one iteration in a "game"....

Labels: International Affairs

Via Luis, Genetic variant in the glucose transporter type 2 is associated with higher intakes of sugars in two distinct populations:

Glucose sensing in the brain has been proposed to be involved in regulating food intake, but the mechanism is not known. Glucose transporter type 2 (GLUT2)-null mice fail to control their food intake in response to glucose, suggesting a potential role for this transporter as a glucose sensor in the brain. Here we show that individuals with a genetic variation in GLUT2 (Thr110Ile) have a higher daily intake of sugars in two distinct populations. In the first population, compared with individuals with the Thr/Thr genotype, carriers of the Ile allele had a significantly higher intake of sugars as assessed from 3-day food records administered on two separate visits...demonstrating within-population reproducibility. In a second population, carriers of the Ile allele also reported consuming a significantly greater intake of sugars...over a 1-mo period as measured from a food frequency questionnaire. GLUT2 genotypes were not associated with fat, protein, or alcohol intake in either population. These observations were consistent across older and younger adults as well as among subjects with early Type 2 diabetes and healthy individuals. Taken together, our findings show that a genetic variation in GLUT2 is associated with habitual consumption of sugars, suggesting an underlying glucose-sensing mechanism that regulates food intake.

Seems like nutrient metabolism & taste preferences are some really important angles for personal genomics; people spend so much time trying to decide what to eat, and arguing about what and how to eat amongst each other. Looks like there's a fair amount of between population difference on this SNP.

Related: Posts on taste and genetics.

Labels: Genetics

A study on the correlation between IL1RAPL1 and human cognitive ability:

This study aimed to investigate the effects of IL1RAPL1 on the human cognitive ability...Results indicated that genotypes of DXS1218, DXS9896 and rs12847959 were associated with memory/concentration factor intelligence quotient (IQ)...DXS1218 also associated with full IQ, verbal IQ, and performance IQ...rs12847959 were related to verbal comprehension factor and perceptual organization factor IQ...Further study on rat brain revealed that Il1rapl was mainly expressed in memory/concentration-associated encephalic regions, such as hippocampus, dentate fascia, osmesis perithelium, and piriform cortex. mRNA expression levels of Il1rapl in brains of rats with different learning and memory abilities showed significant difference. Combined data suggested that IL1RAPL1 affected human cognitive ability to some extent, especially the memory and concentration capability.

Check out the HapMap on that SNP. Remember to wait up on reproducibility here. Sandy has a longer post addressing the radioactivity of such research (obviously he is lying when he says he's an anthropologist; doesn't pass the smell test).

Labels: Genetics, IQ

99% Genetic? Individual Differences in Executive Function Are Almost Perfectly Heritable:

The results from this approach are jaw-dropping: variance shared among each variety of executive function (inhibition, updating, and shifting) is nearly perfectly heritable: the contribution of the "A" component to those correlations is 99%. This heritable variance in the common executive function predicts nearly all of the genetic variance in the inhibition factor, consistent with the idea that those constructs are isomorphic from a heritability standpoint. Second, genetic influences on updating and shifting were roughly half due to the common executive function (43% and 44%, respectively) and half due to unique genetic influences (56% and 42%, respectively). Thus, the overall picture is that executive functions, in both their unity and diversity, are somewhere between 86 to 100% heritable.

I wonder if such high heritabilities imply many adaptive equilibria in terms of personality phenotype with all populations? (remember the rule of thumb that the more heritable a trait is the less fitness implication it has)

Here. The embed is the best bet if you can view it; the download often fails (server has been slammed?). Only a moderate amount of discussion about religion; Dawkins talks a fair bit about an obscure field, evolutionary biology. Well done.

Via Accidental Blogger.

Edward Luttwak has a column (via The Corner) up pointing out that by Muslim measures Barack Obama is an apostate; so it is permissible that he should be killed. This is true, and I think if you asked most Muslims they would accede to the principle here. But as a matter of practicality these sorts of laws aren't enacted or enforced in all circumstances without sensitivity to other parameters; unlike Barack Obama the former president of Argentina, Carlos Menem, converted to Roman Catholicism from Islam as an adult (there have also been African leaders who converted from Islam to Christianity, but I don't believe they visited the Arab world), and he remained on good terms with the Arab nations. If you look at the cases where apostasy is an issue, they seem to fall into two broad categories. The first is one of crass material interest on the part of Muslims and marginality in the case of non-Muslims; in other words, there is a rational reason for a Muslim to use the letter of the law against the apostate or non-Muslim, and that individual who is being persecuted has very little recourse because of their lack of power. Second, there is the perception that the individual is being too vocal and so disrupting social norms and public disorder. It seems from all that I have heard atheism is known and tolerated in the Muslim world so long as atheists remain silent; the problem is public profession of views which go against majority norms. I strongly suspect in the case of the president of the United States most Islamic powers that be would simply ignore the letter of the law (that is, the consensus of Muslim scholars over the ages).

This does not imply that I think the attitudes of Muslims are appropriate to the modern world. Nor do I think it implies that the probability of Obama being assassinated due to his religious history is the same, all things controlled, as someone who had a less complicated past. I'm arguing simply that his "apostasy" really shouldn't be the primary predictor when we consider this issue; powerful men are simply held to different standards in our species, that's culturally invariant and the biggest issue of context in this case.

Addendum: I'm going to take a moment here to make a political comment which I hope won't spawn a thread-closing tirade from readers; but conservatives often complain that liberals don't take cultural complexity into account when they're making models of societies. Additionally, they often accuse liberals of adhering to an idealized noble savage conception of non-Western peoples (e.g., I have heard some liberals argue that Obama's Muslim background will even encourage good feelings from the Islamic world!). Unfortunately, many conservatives are guilty of the same; simple models make good rhetoric and ignorance breeds supreme confidence (I've been guilty of this, you've been guilty of this). But if any individual looks to their own life, their social circle and their culture, they will see a great deal of texture, subtly and nuance which can't be shoehorned into the avowed heuristics.

Labels: Religion

Last year p-ter put up a post pointing to useful online tools such as Haplotter. One of the great things about biology today is that so much of the data from genomics is being thrown out there within reach of the plebs. And a lot of value is being added through user interfaces which smooth the connection between you and these databases. So check out NextBio; from the FAQ:

NextBio is a life science search engine that enables researchers and clinicians to access and understand the world's life sciences information. With NextBio, in just one click you can search through tens of thousands of study results with billions of data points spanning across different experimental platforms, organisms and data types. NextBio also searches across millions of publications to help you find new articles pertaining to your query. NextBio's search engine makes massive amounts of disparate biological, clinical and chemical data from public and proprietary sources searchable, regardless of data type and origin, and empowers scientists to quickly understand their own experimental results within the context of other research.

I'm sure the slick AJAX-driven search tools are a nice Web 2.0+ pitch to investors; but the substantive element is the data. There are only so many researchers with eyeballs in the world; on occasion amateur astronomers can still pick out something new amongst the constellations, and I think to some extent that that sort of dynamic also holds for the amount of unprocessed data that the post-genomic era has made available to us. I really encourage readers of this weblog to poke and prod around the data piles with these new tools; Web 2.0 isn't just YouTube and Facebook....

Related: VentureBeat weighted in a few weeks ago on this company....

Labels: Genomics

Gender Differences in the Mu Rhythm of the Human Mirror-Neuron System:

The present findings indirectly lend support to the extreme male brain theory put forward by Baron-Cohen (2005), and may cast some light on the mirror-neuron dysfunction in autism spectrum disorders. The mu rhythm in the human mirror-neuron system can be a potential biomarker of empathic mimicry.

Don't know enough about this stuff to comment, but figure readers would find it of interest....

Labels: sex differences

Sandy has two posts over at Anthropology.net worth checking out; The sexiness of facial symmetry across cultures and species and Earliest known archaeological evidence of Americans found in Monte Verde, Chile.

Over at The Corner they are discussing an interview series with Tom Wolfe. Wolfe claimed that Charles Darwin was a plagiarist. Derb pushed back. Since they keep talking about the interview, I decided to watch. A few notes....

Wolfe says that Darwin was an obscure man who had a famous grandfather (Erasmus I'm assuming, not Josiah Wedgewood). I don't think this is really right. Unfortunately, we can't run an experiment which deletes Charles Darwin's contribution to science, but before he became the great evolutionary thinker he was a prominent travel writer. The Voyage of the Beagle went through several editions; I'm not sure we would remember Charles Darwin today (how many popular Victorian authors do we remember now?), but he was not an obscure figure in mid-19th century England.

Then he notes that E. O. Wilson believes everything is genetically predetermined. That we have no free will; we can't change our decisions. Wilson, especially during the Sociobiology years offered up a few naive quotes; but as anyone who has wrestled with heritability knows a simple affirmation of genetic determinism is so banal as to be trivial. Wolfe is either overreading, or not communicating the nuance of his genuine thinking.

After this Wolfe goes on to make the distinction between genetic theory and neuroscience whereby the former is literature and the latter is science. He also suggests that the three leading lights of genetic theory are totally unversed in the workings of the brain. Who are these leading lights? E. O. Wilson, Daniel Dennett and Richard Dawkins. Wolfe correctly notes that by training Dennett is a philosopher and Dawkins is an ethologist; so it is peculiar that he considers them leading lights. Wilson is more properly a field ecologist who generally leaves theoretical work to a collaborator (Robert MacArthur or Charles Lumsden for example). Since Dennett is the co-director of the Center for Cognitive Studies at Tufts I assume he stumbles onto neuropsychological material now and then. Obviously Wolfe has fallen into the all too common trap of conflating popularizers with eminent researchers; easy if you don't do your homework. John Maynard Smith, W. D. Hamilton and Richard Lewontin are evolutionary genetic scientists of note; much of Dawkins's thinking is derivative from the first two, while Wilson was influenced by Hamilton, and finally Dennett seems clearly to have had evolution predigested for him by Dawkins. An emphasis on the evolutionary part is critical; from what I know it seems that molecular genetics along the biophysical margins does bleed into neuroscience quite a bit. One of the founding fathers of modern molecular genetics, Francis Crick, spent his last years focused on neuroscience. Wolfe knows this so he really didn't mean to dismiss all genetics as literature; just evolutionary biology. I won't object too strenuously to this characterization, but I will submit that neuroscience today is too young a discipline to be taking on airs. There are many facts strewn about, but it seems that even the skeleton of a theoretical superstructure does not exist to scaffold them into a coherent whole.

Finally, you can check out the second to last interview segment (the last has not been put up yet), Wolfe here is claiming that the emergence of language resulted in a post-evolutionary age for our species. This is false of course; since dismissing genetic theory as literature he hasn't been keeping up on the literature obviously! The whole line of thinking struck me as incoherent, so perhaps I'm missing something. Wolfe also makes a host of extremely disputable assertions about unique human tool use, the rationality of humans and the lack of relation of modern status games with evolutionary genetics.

In any case, I only checked it out because of the gushing in The Corner. I'm a dilettante myself so I wasn't going into it looking to pick out errors, but these seemed to be worthy of correction since obviously many people look to Tom Wolfe as an Authority and keen observer of the world. I'll probably check out his novels; I'm sure he makes up for his sloppy characterization of science with a sharp eye toward fluid prose....

Update: Derb weighs in again.

Continuing my series of notes on the work of Sewall Wright, this one deals with the subject of genetic drift. I had originally planned to call this note 'Inbreeding and the decline of genetic variance', but anyone interested in the matters covered here, and searching for them on the internet, is far more likely to search for 'genetic drift'. This is one of the subjects most closely associated with Wright, to the extent that genetic drift was formerly often known as the 'Sewall Wright Effect'. My main aim is to help people follow Wright's own derivation of his key results, and to clarify the relationship between genetic drift and inbreeding.



I will refer mainly to the papers reprinted in the collection Evolution: Selected Papers, (ESP) and especially the monumental 1931 paper on 'Evolution in Mendelian Populations', which is available online here.
Anyone interested in Wright should also read William B. Provine's biography of him. If in these notes I occasionally make critical remarks on Provine, it should not detract from the general excellence of his book. See the References for details.

In an infinitely large population, in the absence of selection and mutation, the proportions of different gene types (alleles) in the population will remain unchanged indefinitely. But real populations are never infinitely large, and gene frequencies will fluctuate to some extent by chance. As Wright put it in 1931, 'Merely by chance one or the other of the allelomorphs [alleles] may be expected to increase its frequency in a given generation and in time the proportions may drift a long way from the initial values' (ESP, p.107.)

The general nature of drift can be illustrated by the hackneyed example of coin tossing. If we simultaneously toss a number of 'fair' coins, and repeat the trial a large number of times, then the average proportion of heads, by the definition of a fair coin, will be 1/2, and the average number of heads per trial will be N/2, where N is the number of coins in a trial. More generally, suppose the probability of heads for each coin is always p, where p is any fraction between 0 and 1. The long term average number of heads per trial will then be Np. But on any particular trial, purely by chance, the number of heads is likely to deviate from the average. It can be shown that the variance of the number of heads per trial is Npq, where q = 1 - p. [Note 1] If we are interested in the proportion of heads per trial (the number of heads divided by N), it can be shown that the variance of the proportion is pq/N. [Note 2] On each trial, the proportion of coins is therefore likely to deviate from the long term average by a quantity related to pq/N.

Departing now from the real behaviour of coins, let us suppose that the value of p on each trial is determined by the proportion of heads in the previous trial. The proportion of heads will then drift up and down in a 'random walk' pattern, with the size of the 'steps' being inversely related to the size of N. If N is very large, each step will be small, but if N is small the steps may be relatively large. If, by chance, the proportion of heads in a trial ever reaches 1 or 0, then p for all future trials will also be 0 or 1, and heads (or tails) will be permanently 'fixed'. This is very likely to happen sooner or later.

Genes are not coins, so the analogy is not perfect. In a population of genes, the replication of each gene is not a simple matter of 'heads or tails', as each gene may have 0, 1, 2 or more descendants. Also, while the number of coins is assumed to be fixed at N, a biological population is seldom absolutely fixed in size. Nevertheless, there are important similarities. In the absence of selection, it is a matter of chance whether or not a particular gene enters an egg or sperm and then survives to reproduce again in the next generation. Suppose that there are two alleles, A and B, at each locus, with the frequencies p and q in the population. In the absence of selection and mutation, these will also be the expected frequencies in the next generation. In a population of N diploid individuals, there are 2N genes in the population at each locus. In a stable population there will still be 2N genes in the next generation. We can schematically represent reproduction as a 'trial' consisting of 2N events, each involving the random choice of a gene to enter the new generation, with probabilities of p and q for the 'outcomes' A and B at each choice. The probabilities of obtaining the various possible combinations of A's and B's are then given by the expansion of the binomial (p + q)^2N. Wright himself uses this model of the process on several occasions, e.g. ESP p.289. While this may seem a very artificial way of viewing reproduction, it is not as unrealistic as it seems. Suppose that N diploid individuals each have the same number of offspring, the number being large, and certainly large enough to ensure that there are at least 2N copies of each allele among the population of offspring. Then select N of the offspring as 'survivors', completely at random, which is analogous to survival in a resource-limited population without natural selection. The probability of the various possible gene frequencies will then be approximately as in the schematic model (with the complication that in a finite population of offspring the probability of selecting an offspring with a given allele will be affected by the number already selected, e.g. if nearly all the alleles of a given type have, by chance, already been selected, the probability of selecting another one will be much reduced).

Nothing has so far been said about inbreeding. Moreover, the processes just described would apply not only to sexually reproducing organisms but also to asexually reproducing organisms and genetic elements, such as mitochondria and Y chromosomes, where the possibility of inbreeding does not arise. But in Wright's treatment of the subject, references to inbreeding are frequent, and the rate of genetic drift is derived by an argument which seems to depend on the existence of inbreeding. For example, on p.165 of ESP he says: 'If the population is not indefinitely large, another factor must be taken into account: the effects of accidents of sampling among those that survive and become parents in each generation and among the germ cells of these, in other words, the effects of inbreeding'. Such statements are likely to give the impression that inbreeding is fundamental to the process of genetic drift. How can this be?

The explanation is that in a sexually reproducing population a convenient measure of genetic drift is the changing proportion of homozygotes, and the existence of homozygotes is related to inbreeding. If a given allele has ultimately arisen from a single mutation, then homozygous copies of that allele can only occur in the same individual if that individual is descended from the same ancestor by at least two paths, which is by definition inbreeding. Even if the allele has more than one origin, the level of inbreeding in the population will affect the level of homozygosis. But as the example of asexual organisms shows, there is no necessary connection between genetic drift and inbreeding. R. A. Fisher, in his different approach to the subject, does not (I think) ever refer to inbreeding. Confusing the two things would be like confusing the study of heat with the study of thermometers.

It may therefore be wondered why Sewall Wright took his particular approach. The answer may be partly that his mathematical training was less advanced than Fisher's, so that he was obliged to use less mathematically sophisticated methods. This has the advantage that his work on the subject is in principle accessible to a wider range of readers. Moreover, on one important point Wright's methods got the correct result where Fisher, through neglecting a quantity which turned out not to be negligible, got the wrong result by a factor of 2 (as Wright never tired of pointing out). But I think the main reason for Wright's approach was that he first investigated genetic drift in the context of agricultural breeding, where livestock are often closely inbred. In this context one of the main concerns is to quantify the loss of genetic variation in each particular inbred strain. It was therefore natural for Wright to approach the subject by measuring the loss of heterozygosis associated with inbreeding. When he later turned to consider genetic drift in natural populations, where mating is approximately random, he continued to use the methods he had already devised for the study of inbreeding in agriculture. (I will not now explore the precise meaning of Wright's coefficients of inbreeding (the famous F-statistics) which I hope to deal with in another note.)

Wright's most important finding was that heterozygosis (the proportion of heterozygotes in the population) tends to decline at a rate of 1/2N per generation, where N is the diploid population size. (This assumes that males and females each have a population size of N/2.) Most textbooks give a simplified version of Wright's derivation of this result. Wright's own treatment, in EMP, is difficult to follow, and in view of its importance I have provided a guide in Note 3 below.

Even the simplified textbook versions are not always very clear, and I do not know of any wholly satisfactory account. Key assumptions are often not clearly stated or justified. Two relatively good accounts are those of Falconer and Maynard Smith (see Refs.) I will outline a derivation based mainly on Falconer (with some modifications).

Let us assume there is a population of N diploid individuals. Generations are separate. There is no mutation or natural selection in the period under consideration. The n'th generation is designated Gn, the previous generation by Gn-1, the following generation by Gn+1, and so on. The probability that the two genes at the same locus in an individual of Gn are identical is designated CIn, where CI stands for 'coefficient of inbreeding'. (For my approach here it is not necessary to specify whether the genes are identical 'by descent'.) The probability that two randomly selected genes at the same locus in two different individuals of Gn are identical is designated CKn, where CK stands for 'coefficient of kinship'.

For the simplest case, consider a population of hermaphrodites which are capable of self-fertilisation and mate completely at random, including with themselves. (This would be approximately true of some marine invertebrates which release gametes into the water.) From the assumptions of random mating and non-selection it follows that any individual in Gn is equally likely, with probability 2/N, to be a parent of any individual in Gn+1 (since in a stable population each individual will have on average have 2 out of the N surviving offspring). It does not follow that, if we select at random an individual in Gn+1, and then select another, there is a probability of 2/N that the second individual will have the same father (or mother) as the first. For example, if each individual in Gn produced exactly 2 surviving offspring, the probability that a second randomly selected individual in Gn+1 had the same father (or mother) as the first would only be 1/(N-1). To get a probability of 2/N we require an additional assumption, which is technically satisfied by specifying that the number of offspring for individuals follows a Poisson distribution. (This assumption is mentioned by Maynard Smith but not by Falconer.)

With these assumptions, it follows that CIn equals CKn. In the case of CIn, we select a gene at random in Gn, and then inquire whether the other gene at the same locus in that individual is identical. In the case of CKn, we select a gene at random in Gn, and then inquire whether another randomly selected gene at the same locus in a different randomly selected individual is identical to the first gene. But in both cases each gene is a copy of a gene taken absolutely at random from all the genes in Gn-1. The probabilities of identity are therefore the same, and CIn therefore equals CKn. By the same argument it follows that any two randomly selected distinct genes at a locus in Gn have the same probability of being identical, whether they are in the same or different individuals. If we call this probability CDn, we have CDn = CIn = CKn, for any value of n. But CIn can be broken down into two component probabilities. With probability 1/2N, the two genes at a locus in the same individual are copies of the very same gene in Gn-1, in which case they are certainly identical. In all other cases, therefore with probability 1-1/2N, they are copies of two distinct genes in Gn-1, in which case there is a probability CDn-1 that they are identical. But CDn-1 = CIn-1 (since the equality CDn = CIn applies for any value of n). The total probability CIn therefore comes to CIn = 1/2N + (1 - 1/2N)CIn-1. The coefficient of inbreeding in one generation is therefore derivable from the coefficient in the previous generation by a formula involving the addition of 1/2N. It can further be shown, with a little algebraic manipulation, that heterozygosis tends to decline by a factor of (1 - 1/2N) per generation (see Falconer p.64-5 for a proof).

If self-fertilisation is excluded, two genes in the same individual cannot be copies of the very same gene in the previous generation, so the analysis needs to be pushed further back. If mating between different individuals is completely random, including siblings, then CIn = CKn-1. If mating between siblings is excluded, but otherwise random, CIn = CKn-2, and so on. But it is always possible to express the 'coefficient of inbreeding' in one generation in terms of the coefficients in previous generations, and heterozygosis always tends to decline by a factor of (1 - 1/2N) per generation (assuming equal numbers of males and females).

The above argument, like Wright's own, measures the progress of genetic drift by the decline of heterozygosis and the associated increase in the coefficient of inbreeding. It should however be clear that this is not essential. If we wanted to study genetic drift in asexual haploid replicators, such as Y chromosomes, it would be possible to modify the derivation to use only coefficients of kinship, rather than inbreeding. More fundamentally, the process of genetic drift depends not on inbreeding but on the existence of variance in reproductive success. Some genes have no descendants, some have only one, and some have more than one. Over the course of time, more and more lines of descent die out, and the surviving genes are collectively descended from fewer and fewer original ancestors. Ina sexually reproducing population this also leads to increased levels of inbreeding, in a broad sense. If there were no such variance in reproductive success - if every gene had exactly the same number of surviving 'offspring' - there would be no genetic drift. Among diploids, the variance in replication of individual genes is due to two factors: the variance in the number of surviving offspring, and the random allocation of genes to gametes in the process of meiosis. Even if every diploid individual had exactly the same number of surviving offspring, there would still be variance in the replication of individual genes for the second reason. As for the variance in the number of offspring, the assumption of a Poisson distribution is probably not unreasonable in many species, but there could be departures from it in both directions (i.e. either greater or smaller variance). There might also be different variance in the two sexes. For example, among animals like Elephant Seals, the variance among females might be rather small, because all females have a low but steady rate of reproduction, whereas among males the variance would be much higher, as many males have no offspring at all, while a few have a large number. Wright takes account of some of these factors in his discussions of 'effective population size',

This note has only dealt with a few aspects of Wright's work on genetic drift. I have tried to identify the underlying assumptions and (in Note 3) to clarify Wright's most important derivation. None of this says anything one way or the other about the actual importance of genetic drift in evolution. What should be clear is that genetic drift is a weak force except in very small populations, since its effect is inversely proportional to population size. In large populations it would be overpowered by modest rates of selection or migration. (The other factor to consider is mutation, but except in large populations this is an even weaker force than drift, as mutation rates are typically of the order of only 1/100,000 per generation.) I hope to deal with some of these issues in further notes.


Note 1: Suppose we toss a single coin K times, where K is a large number. If the probability of heads is p, the total number of heads will be Kp and the average number of heads per toss will be Kp/K = p. But on each particular trial (the toss of a single coin) there can only be 1 or 0 heads, so we will have Kp trials with the deviation value (1 - p), and K(1 - p) trials with the deviation value (0 - p) = - p. Using the abbreviation q for (1 - p), the variance of the number of heads for trials consisting of a single coin toss is therefore [Kpq^2 + Kqp^2]/K = pq^2 + qp^2 = pq(q + p) = pq. It may seem odd to speak of the variance of the number of heads in trials where there is only one coin per trial, but in principle it is legitimate, and it enables us easily to derive the variance of the number of heads where the trials involve N coins. Since the variance of the sum of a number of independent numerical values equals the sum of the variances of the values individually, the variance of the number of heads in N independent coin tosses, each with variance pq, is simply Npq.

Note 2: The average proportion of heads per trial of N coin tosses, each with probability p, is in the long term p. If X is the number of heads in any particular trial of N coins (where X is a variable), the deviation values of the proportions will be of the form X/N - p = (X - Np)/N, and the variance of the proportions in K trials will be S[(X - Np)/N]^2]/K. But S[(X - Np)/]^2]/K is the variance of the number of heads, which has been proved equal to Npq, so the variance of the proportion is Npq/N^2 = pq/N.

Note 3: This is a commentary on pages 108-110 of ESP, which reprints pages 107-109 of the original paper EMP (the near identity of pagination is just a coincidence). I will mainly be concerned with page 109 of ESP, where Wright derives his fundamental results for the decline of heterozygosis. In following the derivation it is necessary to refer back frequently to the definitions at the bottom of page 108.

Wright assumes that the sexes are separate (so there is no self-fertilisation) but that mating is otherwise completely random, including between siblings. He assumes that there are Nm breeding males and Nf breeding females. With random mating, he states that the proportion of matings between full siblings is 1/NmNf. This evidently assumes that there is a probability of 1/Nm that two mates have the same father, and an independent probability of 1/Nf that they have the same mother (note that m and f stand for male and female, not mother and father). This is actually a strong assumption, which ought to be clearly stated. It assumes (a) that the number of offspring of individuals follows a Poisson distribution (or something similar) and (b) that parents have male and female offspring in the same proportions as in the population generally. This is not necessarily true: for example if some parents had a strong bias towards producing male or female offspring, the probability of mating between siblings would be reduced. (Wright does discuss some of these considerations in the section on 'The Population Number' at pp.111-12 of ESP.)

Wright then gives the proportion of matings between half siblings, and between all less closely related individuals. These depend on the same assumptions as for full siblings.

He then gives a formula for M, the correlation between mates in the current generation. Note that the formula is of the form a'^2b'^2[Z], where Z is a complicated expression in square brackets. From the definitions on p.108 we have a'^2b'^2 = [1/2(1 + F')][(1 + F'')/2], so we have M = [1/2(1 + F')][(1 + F'')/2][Z]. The expression Z can be derived by Wright's method of path analysis. The first component of Z deals with the case of mating between full siblings. If we label the siblings A and B, and their parents C and D, we have two 'direct' paths, ACB and ADB, and two 'indirect' paths, ACDB and ADCB, which involve the correlation M' between mates in the previous generation. Hence the coefficient (2 + 2M') for the first component. For half siblings A and B, there is one shared parent C and two non-shared parents D and E, so there is one direct path, ACB, and the three indirect paths ADCB, ADEB, and ACEB, giving the coefficient (1 + 3M'). For unrelated mates A and B, with the non-shared parents C, D, E and G (to avoid using F, which is already in use), we have no direct paths and four indirect paths, ACGB, ACEB, ADEB, and ADGB, giving the coefficient 4M'.

Next Wright derives an expression for F, the correlation between uniting gametes in the current generation. Here we must note from p.108 that F = b^2M, and b^2 = (1 + F')/2. Using the expression M = [1/2(1 + F')][(1 + F'')/2][Z], we therefore have F = [(1 + F')/2][1/2(1 + F')][(1 + F'')/2][Z] = [(1 + F'')/8][Z]. With a little manipulation, and using the full expression for Z, this can be put in the form F = (1 + F'')[Nm + Nf - M'Nm - M'Nf + 4F'NmNf]/8NmNf . But now we should note that M' is the correlation between mates in the previous generation. We can therefore adapt the equation F = b^2M to get the corresponding equation for the previous generation, i.e. F' = b'^2M'. But b'^2 = (1 + F'')/2, so F' = [(1 + F'')/2]M', and therefore M' = 2F'/(1 + F''). Substituting 2F'/(1 + F'') for M' in the equation F = (1 + F'')[Nm + Nf - M'Nm - M'Nf + 4F'NmNf]/8NmNf, it follows by some grinding but essentially routine algebra that F = Q, where Q is the expression on the right of the second equation on page 109. Then using the definition of P, P', etc, in terms of F, F', etc, the third equation also follows by routine algebra.

This leaves the final death-defying leap to the fourth equation. This is not helped by the puzzling statement that we can equate P/P' to P/P''. This would imply that the proportional change per generation was not just constant but zero, and P/P'' must surely be a misprint for P'/P''. (The fact that this horrible error is not corrected or commented on in the ESP reprint leaves me wondering how closely Provine, as editor, has followed the details of Wright's text.) But even with this correction, it is far from obvious how Wright derives his fourth equation. I had given up hope of solving it until I was reading volume 2 of EGP, and found a discussion of the simpler case of random mating hermaphrodites, which fills in a few gaps in the derivation (see EGP vol 2, p.194-5). First, it confirms the suspicion that P/P'' should be P'/P''. Second it shows (or at least hints) how the problem can be reduced to a quadratic equation. Taking these hints, we can apply them to the fourth equation on p.109. First, rearrange and simplify the third equation to get P - P'[1 - (Nm + Nf)/4NmNf] - P''(Nm - Nf)/8NmNf = 0. Then divide through by P'' to get P/P'' - (P'/P'')[1 - (Nm + Nf)/4NmNf] - (Nm - Nf)/8NmNf = 0. But by assumption P/P' = P'/P'', so P/P'' = (P'/P'')^2 = (P/P')^2. We can therefore treat the equation as a quadratic of the form ax^2 + bx + c = 0, with x = P/P'. This can be solved by the standard method to get (as the larger of the two roots) P/P' = (1/2)[1 - (Nm + Nf)/4NmNf)] + (1/2)[root(1 + [(Nm + Nf)/4NmNf]^2)]. This is nearly Wright's fourth equation. For the final step, we take deltaP to mean P - P', so that - deltaP/P' = - (P/P' - 1). We therefore need only subtract 1 from the expression (1/2)[1 - (Nm + Nf)/4NmNf)] + (1/2)[root(1 + [(Nm + Nf)/4NmNf]^2)], and then reverse the sign, to get Wright's fourth equation.

After this tortuous derivation, the discussion on page 110 of ESP is relatively plain sailing. The only slight puzzle is how Wright gets the approximation at the top of the page. I deduce that he uses the fact that when a is a small fraction, root(1 + a) is approximately equal to 1 + a/2. Taking [(Nm + Nf)/4NmNf]^2 as a, and grinding through the algebra, Wright's approximation can then be verified.

Overall, as often with Wright's work, I am torn between admiration for his ingenuity and frustration at his obscurity.

References:

D. S. Falconer: Introduction to Quantitative Genetics, 3rd edn., 1989. (The 4th edn., by Falconer and Mackay (1995) appears to be the same so far as its treatment of genetic drift is concerned.)

John Maynard Smith: Evolutionary Genetics, 1989.

William B. Provine: Sewall Wright and Evolutionary Biology, 1986.

Sewall Wright: Evolution: Selected Papers, edited and with Introductory Materials by William B. Provine, 1986.

Sewall Wright: 'Evolution in Mendelian Populations', Genetics, 16, 1931, pp.97-159. (Reprinted at pp.98-160 of ESP.)

Sewall Wright: Evolution and the genetics of populations, 4 vols., 1968-1978.

Labels: Burbridge, Population genetics

In the comments here, rosko points me to a study on the effects on MC4R, a gene implicated in natural variation in human weight, on pathways involved in sexual function. It's well known, of course, that genetic pathways can be involved in multiple physiological processes--in particular, signaling pathway can generate many different phenotypes depending on what the downstream target of the signal is.

The effects of MC4R simulation in humans are, as rosko comments, kind of interesting:

Methods. Ten subjects were enrolled in a double-blind, placebo-controlled, crossover study. Melanotan II (0.025 mg/kg) and vehicle were each administered twice by subcutaneous injection; real-time RigiScan monitoring and a visual analog were used to quantify the erections during a 6-hour period. The level of sexual desire and side effects were recorded with a questionnaire.

Results. Melanotan II initiated subjectively reported erections in 12 of 19 injections versus only 1 of 21 doses of placebo. The mean rigidity score of the responders was 6.9 on a scale of 0 to 10. The mean duration of tip rigidity greater than 80% was 45.3 minutes with Melanotan II versus 1.9 for placebo (P = 0.047). The level of sexual desire after injection was significantly higher after Melanotan II administration than after placebo. Nausea and stretching/yawning occurred more frequently with Melanotan II, and 4 of 19 injections were associated with severe nausea.

I wondered what a "Rigiscan" is--find out here. Hypothetically, one could test whether natural variation in sexual behavior in humans is also affected by MC4R polymorphism, though I can't imagine that being a particularly fun study to carry out (one for agnostic's new series? 23andme + free time = association studies about erections).

This reminds of the MC1R story about increased pain sensitivity in redheads in the vague sense that both involve melanocortin receptors and pleiotropy.

Labels: Genetics, Pigmentation

Having already motivated this series, I'll provide the first example of how to put your time to more productive use than participating in the WikiProject G.I. Joe or the still more urgent WikiProject Transformers. If you get interesting results, post them on your blog and provide a link in the comments here. I'll gather up all the results after awhile and summarize them in a follow-up post.

Purpose

Cultural transmission has often been described verbally as viral. Mathematical models of culture incorporate this idea by borrowing epidemic disease models from biology. The goal here is to see if data on "viral videos" support the infectious model of culture.

Pre-requisites

To collect and analyze data: high school algebra, including familiarity with exponentials and logarithms. To get the theory behind the model: first-semester calculus and preferably an understanding of phase plane methods to study a two-variable system of ordinary differenital equations. [1] No knowledge of biology or culture is needed.

Details

Edelstein-Keshet's Mathematical Models in Biology (pp. 242 - 254) provides a good overview of the most basic models of epidemic diseases, and that's what I'm adapting here. In brief, we track the growth rates of two or three classes of hosts: Susceptibles (S), Infectives (I), and perhaps Recovereds (R). The names mean what you think. In the case of viral videos, you can never undo having seen the video, so we will use a very simple model, illustrated below:


If you haven't seen the video yet, you're Susceptible, while if you have seen it, you're Infective. The idea is that someone who's seen the video tells their friends about it in some way, and their friends watch it in their turn. A Susceptible is turned into an Infective at a rate b, so that this parameter measures the infectivity of the video.

We ignore the part of the population that has immunity to the video -- perhaps because they are not in the target demographic group -- and only track those who could be or are infected. We also assume that on the time-scale that the video spreads, the population is constant in size, which seems realistic in this case.

We can write down a system of differential equations for the above picture:

dS / dt = - bSI

dI / dt = bSI

(The product SI is used as an analogy with chemistry's law of mass action for particles that knock into or interact with each other.)

We notice that dS / dt + dI / dt = 0, which means that S + I = constant, call it N. In other words, if we know the number of Infectives, we automatically know the number of Susceptibles -- it is just N - I. Therefore, we don't have to keep a separate tally of the change in S and can eliminate the first equation. Subsituting S = N - I into the second equation, our system becomes just:

dI / dt = bI(N - I)

Let's make a natural change of variables:

i = I / N

g = bN

So, i is the fraction of the population that is Infective, and the growth rate g has units of inverse time (where b had units of 1 / (people * time)). The equation now only has one variable and one parameter:

di / dt = gi(1 - i)

This is the famous logistic equation, which you may already have seen in the context of saturating population growth or the spread of a favored allele to fixation. (The analogies between these three processes are reflected in their being modeled by the same equation, which underscores the importance of formalizing your intuition.)

At equilibrium, the fraction that is Infective does not change, so di / dt = 0. This happens when either i = 0 or i = 1. When i is between 0 and 1, di / dt is positive, so as long as i is not exactly 0, i will increase as time increases and will ultimately end up at i = 1. In other words, i = 0 is an unstable steady-state since a small increase will push it to i = 1, which is stable.

This model may seem simplistic since it implies that every single Susceptible will be eventually see the video, but that's not so unrealistic when you recall that we're only considering the population of the video's target audience -- in 1993, how many teenagers who had TVs in their homes never, ever saw that Blind Melon video with the bee girl? Some videos may have larger or smaller target audiences, i.e. larger or smaller values of the parameter N.

Getting and Analyzing Data

It is impractical for someone without the funding to survey a large random sample of the target audience to attempt to do so. Therefore, we would measure a good enough proxy: the view count for a YouTube video, tracked over time. Depending on how rapidly you think it will increase, you may want to measure it every 6 hours, or once a day. If it grows logistically, it should accelerate first and then still increase but decelerate until it more or less plateaus, like this the picture in the Wikipedia page on the logistic function.

Ideally, you want to track a video that is the only one of its kind -- if there are multiple copies of the same video, that complicates things somewhat, but you might ignore that (see Further Avenues). For example, if a YouTube celebrity is able to curb reproductions of their videos, you can simply wait until their channel puts out a new video. The infectious process would go something like, "Omigod, So-and-So just put out a new video -- you have to see it!" This would be easier if they update fairly infrequently, so that word-of-mouth transmission were the primary route of infection.

Another idea is to wait for the music video of a popular song to come out, but this requires that you be pretty savvy about music trends, and here the potential of multiple copies is even more serious, as fans download it and upload it themselves.

Fad news items are another source, like when that retarded brat got tasered in the UCLA library. Again, multiple copies of it will probably appear.

Assuming you got something like logistic growth, here's how you estimate the parameters N and b. Well, N would just be whatever the plateau value seems to be, so you'll have to wait for it to do so first. It can be shown that the solution to the logistic equation can be re-arranged to yield:

ln ((N - I) / I) = - bt + ln ((N - I0) / I0)

Where N is the max view count, I0 is the initial view count -- pick some small number -- I is the view count at time t, and b is the infectivity rate. So after you've got a concrete number for N and I0, you'd plot (N - I) / I on a ln scale -- it will be a linear function of t, with y-intercept = ln ((N - I0) / I0) and slope = - b. See what b turns out to be.

Then compare values of N and b for different videos. If N is larger for one, that means the target audience is larger (ignoring the fact that a single person may watch a given video multiple times -- that's true for any video, no matter the target audience's size). If b is larger for one, that means it's more infectious.

Further Avenues

If you really kept this going long-term, you could try to classify the videos you're tracking by category and do an analysis of variance or something to see what accounts for the variation in the target audience size and in the infectiousness of a video. Intuitively, we expect more sensational videos to have higher b -- but a hard analysis might tell us more concretely what types of things count as more sensational. We have guesses about that, but we need data to see if those guesses are right.

To make the model a bit more complex, you could introduce a stochastic component to the growth equation. Right now, it is deterministic: as long as the ball gets rolling, everyone in the target audience will see the video. But when few people have seen the video, chance effects could push one ball up while letting another ball stay put. This is like when several copies of a favored allele are introduced into a population -- some will be lost by drift, while another may be propelled quickly by drift at the start, after which point the deterministic equations take over. You would model it just like the frequency of a favored allele under the combined effects of drift and directional selection.

In the context of viral videos, consider multiple copies of the same music video (again due to fans downloading the video from the official channel and uploading it to their own channel). As the target audience does a search for this video, chance effects may propel one of the copies up very quickly while letting other copies languish with low view counts. In this case, the copy that ends up dominating the market increases even more rapidly than under the purely deterministic model because it got a lucky big initial boost through sheer chance effects.

This is what makes is somewhat inappropriate to compare a video that only has one copy to see vs. a video with multiple copies to see. The winner in the latter group will appear more infectious than the former, since it increases much faster, but part of that higher increase is accounted for by chance.

[1] MIT's Open CourseWare site has a great mathematics section that allows you to teach yourself or brush up on these areas. Especially useful is the course on differential equations, which has a full set of video lectures, solved problem sets, exams, and helpful Java applets. An easy to use phase plane applet is pplane.

Labels: do it yourself studies

I was recently directed to this panegyric on Wikipedia, which claims that editing Wikipedia is a better use of the cognitive surplus that might otherwise be spent watching TV. Like 99% of technology pundits, the author is so out of touch with reality that it is not worth taking him to task in depth. Instead, reading that has moved me to begin a regular column wherein I propose a fairly simple study for someone to carry out and increase our understanding of the world.

In fairness, it is often tough to think of a study to do, or how you would concretely carry it out. But since my soul is a font of generosity, I'm literally giving ideas away. We only have so much time and effort to invest in a project, so I have plenty of ideas that I just don't have time to pursue in any depth. Obviously I will keep what I think are the more original or important ones for myself, but there are several reasons why pursuing seemingly unoriginal ideas is still useful:

1) It gives you good practical experience. If you've never tried to find a good dataset that would answer your question, if you've never tried to analyze and summarize the data, and if you've never interpreted these findings in context for the target audience -- well, time to start.

2) Many supposedly established findings have the smell of academic urban legends because they are based on a single study that used an unimpressive sample size and didn't take into account some obvious confounding factors. Yet once it gets cited, it takes on a life of its own, as no one reads the original but simply "knows that study X showed Y." Replication studies are crucial to figure out if we were right.

3) Most published articles aren't terribly original anyway -- "here's yet another example of natural selection at work!" Still, the more astounding the mountain of evidence becomes, the more convinced we become that we are right. There are probably diminishing returns, though: we don't need yet another study showing that cognitive abilities all correlate with each other, but how pervasive is the influence of IQ -- do smart vs. dumb people prefer different types of art?

4) More mundane studies are easier to carry out, so you're not intimidated by the prospect of hunting down a solution to a Great Big Problem. (And if you liked chasing after Great Big Problems, you'd probably already be in academia or a private institute doing that, or preparing to do so in the near future.)

5) If the original study or idea was done awhile ago, improved technology may allow you to take a more in-depth look at it. For example, computers were pretty pathetic in the 1960s, and I'll be there are scores of dusty studies that would benefit from the power of modern home computers.

6) For mathematical models, the properties of a particular model may be so well known that you couldn't hope to contribute anything new on the abstract level. However, you could provide a novel interpretation of it by showing how it also models a phenomenon that no one has applied it to before. This is especially true for fields were the experts don't have much training in modeling, which tend to focus on human beings. Sociology is a perfect example -- here's a field that assumes the primary unit of society is the group, and that groups conflict and interact, while ignoring the individual differences within each group. This isn't a slight to the field, since there are group dynamics. Sociology cries out for differential equation models, where you ignore individuals and track classes of things, and typically only two or three classes!

7) For the studies that I will propose, the data would not be hard to collect, although the process from start to finish may be laborious (hey, that's life). So, I will not suggest studies that require fancy equipment, hundreds of unpaid volunteer subjects, and so on. If it is applying a well understood mathematical model to some new phenomenon, almost all of the work will already be done. However, I realize that we do have academic readers too, or readers who have graduate student friends in need of a study to publish, so occasionally I will propose something that would require access to many volunteers.

Now, I don't have anything against editing Wikipedia or blogging per se, but let's get very real: most of it is a waste of time, which is why almost no academics do it. There are exceptional areas of Wikipedia, and there are exceptions in the blogosphere -- well, obviously we are, and so are bloggers like Steve Sailer, Audacious Epigone, Half Sigma, Inductivist, and others who obtain and analyze data to answer a question or hunch. If the blog is just a hobby, an afterthought after real work is being done in real life (as with my personal blog), that's OK too.

What I want to see die is the practice of intellectual masturbation, where you only fool your brain into thinking that fruitful work is being done. "Participation" per se is no valid criterion for success -- I can participate in an act of masturbation, perhaps even while participating with others in a circle jerk, but I've only really accomplished something when I've contributed to increasing the fertility rate. Fortunately for everyone, though, the real world offers an abundance of problems begging to be fertilized by the seed of your brain -- get in there and tear that shit up.

Labels: do it yourself studies

For many years, Grey Squirrels (an introduced North American species) has been driving out the indigenous Red Squirrel over most of mainland Britain. But now it is reported that a mutant black variety of the Grey Squirrel is threatening to displace the Greys. Apparently, the black ones have higher testosterone levels, are more aggressive, and more attractive to the lady squirrels. (Don't worry, our White Nationalist readers, this isn't a parable. I think.)

Joking apart, the real interest of this is that it seems to be a case of a single mutation with a relatively conspicuous phenotypic effect having a strong evolutionary advantage, somewhat contrary to Darwin/Fisher orthodoxy. There is of course another example in the case of industrial melanism.

Labels: Pigmentation

Two studies report this week on the association of variation near MC4R with body mass. This is the second convincingly replicated locus to be implicated in natural variation in weight, the first being FTO. There are a couple reasons I find this association interesting.

1. Coding mutations in MC4R are known to cause severe obesity. It's to be expected that less severe mutations (the region of the genome implicated in these studies is likely regulatory) could lead to more subtle effects on body weight, but it didn't have to be that way. And this forms part of a pattern that genes that cause Mendelian forms of a disease are also associated with more common forms as well. Why is this interesting? It suggests that the candidate gene approach to finding allele associated with disease wasn't as flawed as people thought--it's just that they were all severely underpowered (the number of individuals in these studies, for example, tops 60,000).

2. One of the studies performed their association study in individuals of Indian descent. This is one of the first GWA studies to focus on a non-European population--a development that will hopefully continue. Insofar as allele frequencies vary among populations, studies of the same phenotype in different populations may get quite different results (note that studies of skin pigmentation in Europeans don't identify SLC24A5, but studies in South Asians do--the reason is that the relevant variant in the gene is fixed in Europe but at moderate frequency in India). Population genetics has always had a role in the rational choice of study population for association studies, but as all the low-hanging fruit gets taken, this role will perhaps become more pronounced.

Labels: Genetics

For general amusement, see this report from the BBC. (Via John Hawks.)